基于利益相关者理论的投保人与保险人的博弈分析
2012-09-19杨卫平陆凤顺
杨卫平,陆凤顺
(湖南大学 金融与统计学院,湖南 长沙 410006)*
一、引 言
作为当前西方经济学界和管理学界研究的热点理论之一——利益相关者理论,对传统股东利益至上的观点提出了挑战,认为企业是一系列包括股东、管理者、雇员、债权人、供应商、客户等利益相关者之间的多边契约,各利益相关者彼此之间形成一个利益共同体,以自身所拥有的人力资本或非人力资本进行合作,应对外部不确定性环境所带来的风险[1]。依据利益相关者理论,寿险公司的股东、管理者、员工等都是公司的利益相关者,此外,投保人也是寿险企业的主要利益相关者,因为投保人既是寿险公司的消费者,又是与公司长期发展息息相关的主要债权人[2]。目前国内学者对利益相关者理论在保险行业中的运用研究,多集中于对逆选择和道德风险的博弈分析[3,4,6]或是某个险种相关方的利益博弈分析[5,7],侧重对保险公司及其股东利益的保护,而从保护投保人利益角度研究的较少,缺乏对弱势利益相关方利益的关注,特别是对投保人的利益关注不足。
二、保险公司利益相关者的利益需求及其冲突
保险公司的股东、管理者和投保人都是公司的利益相关者,但利益需求各有不同。股东和经营者代表公司的利益,关注的是高额利润和资本的回报,作为利益共同体,经营者为股东利益服务。保险企业是典型的负债经营企业,尤其在寿险公司,寿险合同大多有长期性和持续性的特点,因此,投保人不仅关注公司能否提供优质的产品和服务、合理的产品价格,还关注公司在长期内能否有效履行寿险合同的保障和给付责任。在保险企业经营的过程中,为了获得更高的利润和资本回报,就可能产生危及投保人利益的行为,例如在发生保险事故时,基于晦涩难懂的保单条款作出不利于被保险人的解释;可能采取更激进型投资策略,危害公司偿付能力,从而损害投保人的长期利益等等。公司和投保人之间利益的冲突,是由于各自追求的利益不同。我国保险业起步较晚,使得大多数保险公司仍把短期边际利润作为企业的唯一目标,不注重利益相关者特别是投保人利益的保护,两者的利益冲突问题尤为突出。
三、保险人与投保人的利益博弈分析
(一)静态博弈分析
1.完全信息静态博弈
(1)建模前提:第一,博弈中代表保险人利益的股东是指对公司的利润拥有控制权并对公司的重大事件具有话语权的控制股东,并非指小股东。第二,假设控制股东和经营者已经成为一个利益共同体,即控制股东和经营者利用自己在信息和管理等方面的优势合谋,在博弈模型中将这一利益共同体简称为保险人,将投保人、被保险人和受益人这一利益共同体称为投保人。第三,博弈的局中人——保险人和投保人都是理性人,风险态度是风险规避,在客观条件约束下作出使自身利益或效用最大化的决策。第四,博弈双方的策略空间、特征、支付函数及博弈结构等是共知的。
(2)模型假定:第一,假定为单阶段的静态博弈。即保险人和投保人虽然不是同时采取行动,但是对于保险人的行为,投保人可以观察到,并作出反应。第二,博弈的局中人为保险人和投保人。保险人的策略空间为侵害投保人利益、不侵害投保人利益;投保人的策略空间为投保、不投保。第三,博弈基本参数假设如下:X为投保人选择投保时需缴纳保费;Y为投保人在保险人不侵害其利益时可以获得正常收益(包括赔偿金及分红等投保人理应获得的收益);C为投保人在保险人侵害其利益时获得的收益,(因为保险人可能以投保人不具有可保利益或其他理由拒绝赔偿保险金,还有可能减少分红等,使投保人的收益低于正常情况下的收益);D为保险人在不侵害投保人利益时可以获得的正常收益;T为保险人在侵害投保人利益时可以获得除D以外的额外净收益(此额外净收益为额外收益减去因侵害支付的成本后的净收益,T>0);P3为投保人不将资金用于投保,而将投保费用投资于资本市场可获得的收益,即投保费用的机会成本。保险人侵害投保人利益,投保人选择不投保时,保险人不能获得承保利润和投资收益等收益,但仍需支付侵害造成的成本,包括带来的公司名誉损失E,以及被监管部门查处的罚金F(这里把监管部门对保险人的处罚统称为罚金)。保险人不侵害投保人利益,投保人仍选择不投保时,保险人的收益为-H。建立静态博弈,二者的收益矩阵如表1所示,括号中第一个值表示投保人的收益,第二个值表示保险人的收益。

表1 保险人与投保人的收益矩阵
需要说明的是,现实情况中有(-X+Y)<P3<(-X+C)。因为倘若保险人侵害投保人的利益,例如在投保人索赔时,保险人以投保人不具有可保利益或其他理由拒绝赔偿保险金,投保人则可能拿不到保险金或只能拿到一小部分退保费,故有(-X+Y)<P3;而在投保人利益不被侵害时,投保人可以拿到正常额度的保险金,使得P3<(-X+C),此时投保人才有动力把钱从资本市场取出用以购买保险。
为了讨论简便,再设P1=-X+Y,P2=-X+C,M1=X+D-Y+T,M2=X+D-Y,G1=-EF<0,G2=-H<0。P1即保险人侵害投保人利益时投保人投保的收益,P2即保险人不侵害时投保人投保的收益,M1即保险人侵害时投保人投保保险人的收益,M2即保险人不侵害时投保人投保保险人的收益,G1即保险人侵害投保人不投保保险人收益,G2即保险人不侵害投保人不投保保险人收益。则以上收益矩阵可简化为表2所示。

表2 保险人与投保人的收益矩阵
(3)模型求解。在完全信息条件下,利用划线法寻找以上收益矩阵的纳什均衡:第一种情况:G1>G2时,由以上讨论可知M1>M2(因为M1=M2+T且T>0),保险人最佳策略是侵害,故在M1下面划一横线;同理,在投保人选择不投保时,保险人最佳策略是侵害,在G1下划线,可知保险人的占优策略是“侵害”。当保险人侵害投保人利益时,投保人的最佳策略是不投保,在P3下划线;当保险人不侵害投保人利益时,投保人的最佳策略是投保,在P2下划线,此时有唯一的纳什均衡策略(不投保,侵害)。从上可知,M1、G1下都划线,说明保险人的占优策略是“侵害”,也就是说,不管投保人是否投保,保险人选择侵害都比不侵害能获得更大的收益,那么,保险人就没有动力维护投保人的利益,而在保险人选择侵害时,投保人最佳的选择就是不投保。因此,在完全信息条件下,保险人为了使自己利益最大化,没有动力去保护投保人的利益,投保人也将会选择退出保险市场。第二种情况:G1≤G2时,用划线法可知该博弈矩阵不存在纳什均衡策略。
2.不完全信息静态博弈。现实中的情况是,由于信息不对称,投保人并不确定保险人是否会侵害自己的利益,但知道保险人侵害的概率为α,不侵害的概率为1-α,保险人只能知道投保人投保的概率为β,不投保的概率为1-β,那么对投保人而言,选择投保时的期望收益:U1=αP1+(1-α)P2;选择不投保时的期望收益:U2=αP3+(1-α)P3=P3;总收益:U0=βU1+(1-β)U2=αβP1-αβP2+βP2-βP3+P3。对收益函数求导:即对投保人来说,当保险人侵害其利益的概率大于α时,投保人的最优选择是不投保;当保险人侵害的概率小于α时,投保人的最优选择是投保,即当保险人侵害的概率等于α时,投保人选择投保或不投保效用是一样的。

对保险人而言,侵害投保人利益时的收益为:E1=βM1+(1-β)G1;不侵害投保人利益时的收益为:E2=βM2+(1-β)G2;总收益为:E0=αE1+(1-α)E2=αβM1+αG1-αβG1-αβM2-αG2+αβG2+βM2+G2-βG2。对收益函数求导:
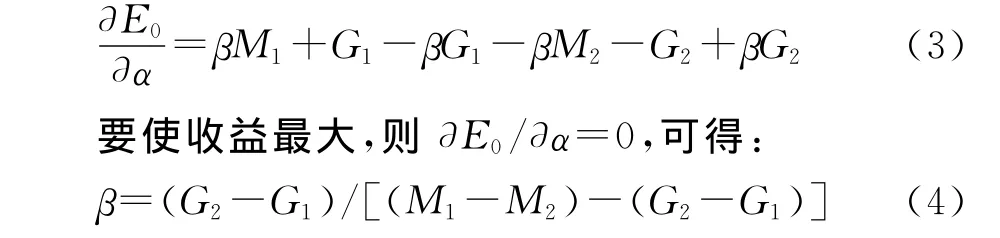
即当投保人选择投保的概率大于β时,保险人的最优选择是侵害;当投保人选择投保的概率小于β时,保险人的最优选择是不侵害;当投保人选择投保的概率等于β时,保险人侵害或不侵害投保人的收益是一样的。
博弈的混合策略纳什均衡解是:保险人侵害的最优概率为α,投保人选择投保的最优概率为β。P2越大,α越小,即投保人在利益不被侵害时可以获得的收益越大,其要求保险人不侵害的概率越小;M1-M2=T越大,β越小,即保险人侵害投保人时得到的不当得利越大,投保人投保的意愿会降低;G2-G1越大,β越大,即保险人将受到监管部门的监管和处罚力度越严厉,投保人选择投保的概率会越大。
(二)完全信息动态博弈模型
1.单一阶段动态博弈。单一阶段的动态博弈属于非合作博弈,假设保险人和投保人都是理性人,作出的选择都是使自己效用最大化为目标。两者之间的博弈是完全信息动态博弈,行动有先后顺序:首先,投保人选择是否购买该保险人提供的保险产品(假设投保人购买保险时即缴纳保费);其次,保险人选择提供高质量或是低质量的产品和服务。投保人购买保险时通常保险人都会承诺客户至上,例如承诺在保单存续期间提供优质服务、发生保险事故时提供快速有效的理赔或人身补偿,类似行为称为提供“高质量产品和服务”,但现实中投保人缴纳了保费之后,保险人有可能不履行合同签订时许下的承诺,例如出险时将事故列为除外责任或以各种理由延缓赔付速度甚至降低保险金额度,类似行为称为“低质量的产品和服务”。
为了简便,称保险人为A,投保人为B,首先,B选择是否购买A提供的保险,然后A选择是否提供优质产品和服务。倘若B不购买保险,效用为0(不能从保险合同中获得效用),倘若购买到高质量的产品和服务,效用为+I1,购买到低质量的产品和服务的效用为-I2,A提供高质量产品和服务可获利润+R1,提供低质量时获利润+R2,其中I1、I2、R1、R2>0,且I1>I2,R2>R1,该博弈的扩展式表述如下:
如图1,在一次性博弈中,利用逆推退归纳法可知,在第二阶段如果B选择投保于A,A的最优策略是提供低质量产品和服务,此时A可获得利润+R2(A选择高质量只能获得利润+R1,而R2>R1),B获得的效用为-I2<0;再逆推至第一阶段,因为B知道如果自己选择投保,A将在第二阶段选择低质量,因此B在追求自身利益最大化的理性假设下,第一阶段的最优选择是不投保(因为选择不投保可得到的效用为0,大于第二阶段的效用-I2),由此可知,均衡结果是B在第一阶段选择不投保结束博弈,博弈的子博弈精炼纳什均衡是(不投保,低质量),即保险人提供低质量的产品和服务,投保人选择不购买保险。若B投保,A提供高质量,则A、B都可获得较高的收益(+I1,+R1)。
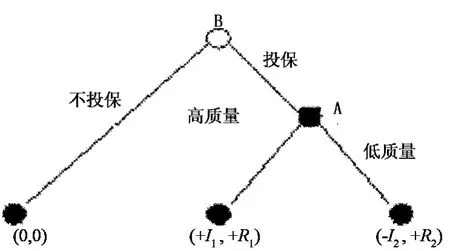
图1 一次性博弈A,B的效用
2.重复博弈。在一次性博弈中,参与人只考虑当期自己可获得的最大收益,无需考虑长期,但是在现实保险市场中,保险人需要考虑长远利益,把保持名誉视作长期利益,因为好的名誉会吸引更多的人加入保险。保险人和投保人之间的动态博弈可以用重复博弈进行分析,这一模型解释如下:
在保险市场交易中,保险人是长期的固定参与人,不断重复提供保险产品,而消费者即投保人是不固定的,为简单起见,假定只有一个保险人A提供保险产品,潜在投保人有B1,B2,B3…,Bn,每个阶段只有一个投保人且每人只购买一次保险产品。A首先与B1博弈,然后与B2,以此类推至Bn,Bn在决定是否投保于A时,了解A的历史,即了解A提供给之前投保人的产品和服务的质量,如果Bn了解到A之前为Bn-1个投保人提供的是低质量,A的名誉败坏且不能回复,Bn也不再购买保险。B1,B2,B3…,Bn只关心自己的利益,A与B1,B2,B3…,Bn博弈的收益分别为U1,U2,U3…,Un,A的总收益 U(n)是所有阶段博弈收益折现值之和,即:
U(n)=U1+εU2+ε2U3+…+εn-1Un,其中ε表示贴现值。
在一次性博弈中,我们已经讨论了唯一的纳什均衡是(不投保,低质量)。但是在无限次博弈中,博弈过程没有最后阶段,不能采用逆向归纳法求解,A不仅仅要考虑短期收益,更要注重其长期收益。在第一阶段,B1选择投保,如果A提供高质量的产品和服务,随后的B2B3…Bn会愿意继续投保;如果A提供低质量产品和服务,之后的潜在投保人将不再投保。均衡结果是(投保,高质量),此时每个投保人得到的效用为+I1,A每一阶段得到的平均效用为+R1,对均衡结果分析如下:
(1)A选择高质量是最优策略。因为A如果选择提供低质量,可以得到的效用为R2,但在之后每阶段的效用为0(因为之后不再有投保人购买保险),如果总是提供高质量的产品和服务,每阶段得到效用R1,效用总和为:
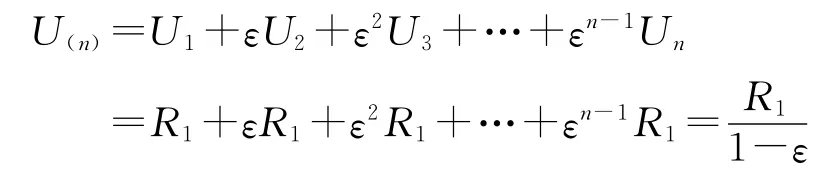
因此,如果保险人提供高质量的总效用R1/(1-ε)大于提供低质量时的效用R2,即ε>(R2-R1)/R2时,保险人就不该选择提供低质量产品和服务。
(2)对于B,假定ε>(R2-R1)/R2。B只关心自己得到的效用,当预期得到高质量产品和服务时才会投保;B预期不曾提供低质量的保险人将会继续提供高质量,所以选择投保是最优的;如果B了解到A提供过低质量的产品和服务,预期A将继续提供低质量,此时不购买是最优的。
四、总结与启示
由以上博弈结果分析可知,投保人作为保险企业的消费者和债权人,其利益的保护和保险企业的长期发展息息相关。如果投保人利益得不到有效的保障,投保人会选择退出保险市场,这将影响到保险企业的市场占有率、良好的企业信誉和形象等等,给保险企业的长期健康发展带来威胁。因此,保险企业在经营过程中要注重有效保护处于弱势地位的投保人的利益,平衡两者之间的利益关系。保险人应该把保持名誉视作长期利益,以客户为导向,在保险条款的解释上更明晰,费率厘定更科学,提供高质量的保险产品和服务,形成良性循环。此外,有效保护投保人的利益,还需要监管部门加大对保险企业的监管力度和处罚力度,以降低保险企业侵害投保人利益的动机,从而有效保护投保人的利益。
[1]陈宏辉.企业的利益相关者理论与实证研究.浙江大学博士论文[D].2003.
[2]彭雪梅.保险会计学[M].成都:西南财经大学出版社.2010:6-7.
[3]顾力.我国保险市场的信息不对称问题研究[D],浙江大学硕士学位论文,2005.
[4]陈桂柳.保险市场非对称信息的博弈分析[D],厦门大学硕士学位论文,2006.
[5]张娇.商业健康保险中道德风险的博弈分析[D],复旦大学硕士学位论文,2007.
[6]杨美琴,龚日朝.保险公司与投保人的静态博弈分析[J],南华大学学报,2008,(4):76-82.
[7]黄亚林.农业保险市场利益相关者的博弈分析[J],金融发展研究,2009,(2):80-83.
