基于自适应Bilateral滤波的SAR图像相干斑抑制

李光廷 禹卫东

①(中国科学院电子学研究所 北京 100190)

②(中国科学院研究生院 北京 100049)

1 引言

SAR图像相干斑的存在给SAR图像的理解与解译带来了极大的困难，相干斑抑制研究也一直是SAR图像处理领域的重要课题。研究SAR图像相干斑抑制的目的是在平滑斑点噪声的同时较好地保持图像的细节信息，至今已有许多经典算法取得了较好的滤波效果[1]。在实际中常用的滤波算法有Lee滤波，Kuan滤波，Frost滤波，Gamma MAP滤波及其它们的改进算法等的空域滤波，还有以小波变换为主的变换域滤波。空域滤波通常对图像中的同质区域有着较好的去斑效果，而边缘等细节区域的保持则不够理想。在小波域滤波中，多种具有良好2维线奇异性刻画能力的二代小波备受关注，但小波域滤波普遍存在伪吉布斯效应明显、阈值选择困难等问题，其中一类非下采样 Contourlet变换(NonSubsampled Contourlet Transform,NSCT)近几年比较受重视，由于它具有平移不变性可以大大降低伪吉布斯效应在相干斑抑制方面已经得到了应用[2,3]。由上面分析可见，相干斑抑制研究的关键在于如何充分利用像元周围的结构信息，从而在平滑噪声的同时来保持图像细节。

本文研究的 Bilateral滤波器[4]是由 Tomasi和Manducci从直觉意义上提出一类空域滤波器，自提出以来许多学者对它进行了理论研究，完善了它的数学基础[5,6]。由于Bilateral滤波器在滤波过程中同时利用中心像素与邻域像素的空间相似性与灰度相似性来计算邻域像素的权值，可以在平滑噪声的同时较好地保持图像细节，因此在图像处理方面得到了越来越广泛应用[7-9]。近年来，该算法被引入到了SAR图像相干斑抑制的研究中[10]。由于Bilateral滤波器在计算图像空间相似性与灰度相似性时均采用高斯函数，而高斯函数的方差系数选择比较困难，文献[9,10]对这一问题进行了研究。文献[9]发现最优的距离方差系数与图像的噪声标准差呈正比，而最优灰度方差系数对图像噪声并不敏感；文献[10]提出了一种利用等效视数及边缘保持指数分两步进行两个方差系数选择的方法。文献[10]的方法取得了较好的相干斑抑制效果，但在进行方差系数选择时计算量大，且最终选用恒定的方差系数。

由于相干斑的乘性特性，分析发现进行SAR图像滤波时两个方差系数设为定值是不合理的。针对这个问题，本文提出了一种自适应Bilateral滤波器；在进行空间相似性度量时，根据图像的局域变差系数来选择局域方差系数；在进行灰度相似性度量时，利用SAR图像的似然概率函数作为度量模型；分别从两方面解决了两个方差系数选择困难的问题。

2 Bilateral滤波器

Bilateral滤波器通过对窗口内不同像素设定不同的权重来进行中心像素值的估计，不同像素的权重由像素间的空间距离与灰度距离共同决定。给定输入图像f，则输出h为

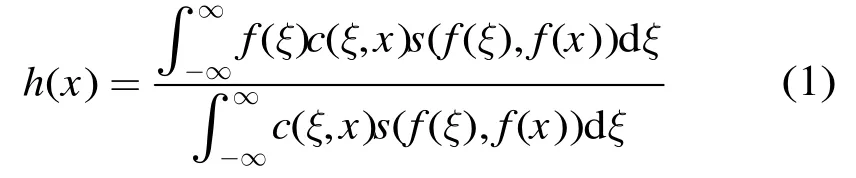
式中分母为归一化系数。其中x=(x1,x2)代表中心像素的坐标，ξ=(ξ1,ξ2)是像素x的一个相邻像素，c(ξ,x)和s(f(ξ),f(x))为两像素的空间相似性与灰度相似性，两个常用的相似性度量模型均为高斯函数

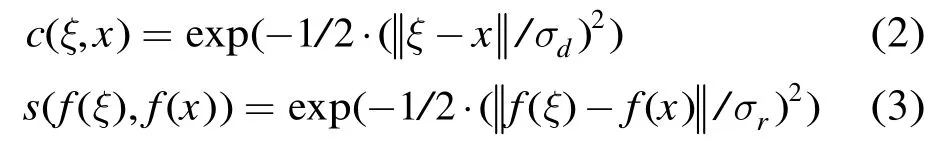
σd,σr分别为空间方差系数与灰度方差系数。

方差系数是高斯函数的形状参数。对空间相似性来说，由式(2)可知，σd越大，则c(ξ,x)随着空间距离增加而衰减的速度越慢，相反则越快。传统的Bilateral算法在滤波过程中采用恒定的σd，这存在如下问题：若σd较大，则邻域像素权值较大容易带来细节的模糊；若σd较小，则邻域像素的权值较小使得同质区域的去噪能力又太差。因此，最优σd的选择与区域的同质性有关，对同质性较强的区域应该选择较大的σd来增强算法的噪声平滑能力，对边缘等同质性较弱的区域则应该选择较小的σd来进行细节的保持。

对SAR图像的灰度相似性来说，用高斯函数作为度量模型是不合理的。具体分析如下：多视SAR幅度图像的相干斑通常用均值为1且服从均方根伽玛分布的乘性噪声来建模[11]，设g为真实灰度值，n为噪声，则f=gn。对L视幅度SAR图像，噪声的概率模型为

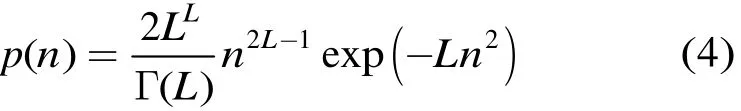
用高斯函数度量两像素的灰度相似性时，相似性仅由像素的灰度差决定。以灰度差为50的两组像素来说明，由式(3)得s(60,10)=s(60,110)，而由式(4)得p(60/10)≪p(60/110)，因此，用高斯函数来度量SAR图像的灰度相似性是不合理的。分析还发现，若通过对数变换将乘性噪声变为加性噪声，由于变换后的噪声仍然是非高斯的，所以用高斯函数来度量对数变换后 SAR图像的灰度相似性也是不精确的。

综上可得，当直接用Bilateral滤波器进行SAR图像相干斑抑制时存在空间方差系数选择困难和灰度相似性模型不合理的问题。针对这两个问题，本文提出了一种自适应Bilateral滤波算法。

3 自适应Bilateral滤波器

3.1 基于SAR图像变差系数的空间方差系数选择

如上一节分析，用 Bilateral滤波器进行 SAR图像相干斑抑制时，空间方差系数σd的选择应该与区域的同质性有关。因此，我们可以建立σd与区域同质性的对应关系，从而根据区域的同质性来选择σd。变差系数是 SAR图像同质性测量最常用的指标，本文仍然用变差系数来进行区域的同质性测量。变差系数CV的计算公式为

式中var(f(x)),E[f(x)]是窗口内像素的方差和均值。

Lopes等人[12]根据两个标准差Cu与Cmax将图像分为3类区域：第1类满足CV≤Cu，为均匀区域，是滤波过程中需要平滑的区域；第2类满足Cu＜CV＜Cmax，为含有一定纹理信息的区域，是过度区域；第3类满足CV≥Cmax，为非均匀区域，大多为图像的细节，是需要保持的区域。其中

由对方差系数的分析知，方差系数σd与变差系数CV应成反比关系，本文所选的模型为

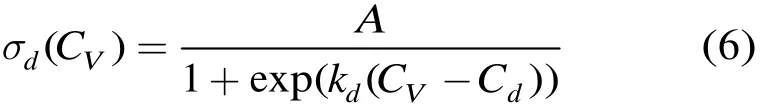
式中A,kd与Cd为待定参数，以滤波窗长N=7为例，参数确定过程如图1所示。

由式(2)知，c(ξ,x)随着两像素空间距离的增加而减小，以0.5作为c(ξ,x)的阈值，3个未知参数按如下思路来确定：对第1类区域，当/2时，c(ξ,x)≥0.5，并且当CV=Cu时等号成立，如图1(a),1(b)中菱形所注；对第3类区域，当时，c(ξ,x)≤0.5，并且当CV=Cmax时等号成立，如图1(a),1(b)中方形所注。将上述等式成立时的条件代入式(2)得

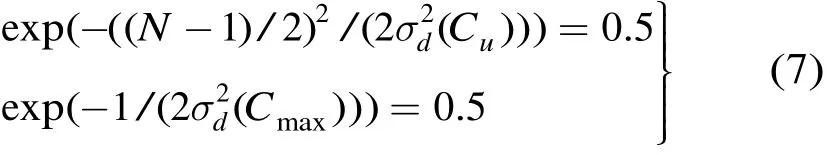
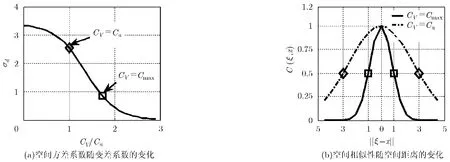
图1 模型参数的确定

解式(7)可得σd(Cu)与σd(Cmax)。结合式(6)所示模型的对称性得

将σd(Cu)与σd(Cmax)代入式(6)并结合式(8)可求解3个未知参数，从而便确定了式(6)。

3.2 基于SAR图像似然概率函数的灰度相似性度量

如第2节分析，用高斯函数作为SAR图像的灰度相似性模型是不合理的。根据式(4)及相干斑的乘性模型可以得到f对g的似然概率函数[13]。本文用该似然函数进行邻域像素与中心像素的灰度相似性度量，由此得到新的灰度相似性模型为

对于L视幅度SAR图像，分析式(9)可以发现，s(f(ξ),f(x))由f(x)和f(ξ)/f(x)共同决定。但对当前像素x来说，f(x)是定值，式(1)中分母的归一化操作消除了f(x)对s(f(ξ),f(x))的影响，如图2(a)所示。因此，s(f(ξ),f(x))只与f(ξ)/f(x)有关，这与相干斑的乘性性质是一致的。

为了说明用似然函数来度量SAR图像灰度相似性的合理性，仿真产生了灰度值为50和150的两幅4视幅度SAR图像，并分别对它们的概率密度进行了统计，如图2(b)中‘3-﹡’所示；分别用似然函数与高斯函数(σr=60)来度量图像的灰度相似性，如图2(b)中‘1-﹡,2-﹡’所示。由图可以看出，用似然函数度量的图像灰度相似性更接近仿真图像的概率密度分布，因此用似然函数作为SAR图像的灰度相似性模型更合理。

3.3 自适应Bilateral滤波器的实现

根据前面的分析，自适应Bilateral滤波器的实现步骤可总结为

步骤1 输入图像，设置窗长N。

步骤2 若图像视数L未知，计算等效视数ENL代替视数L。

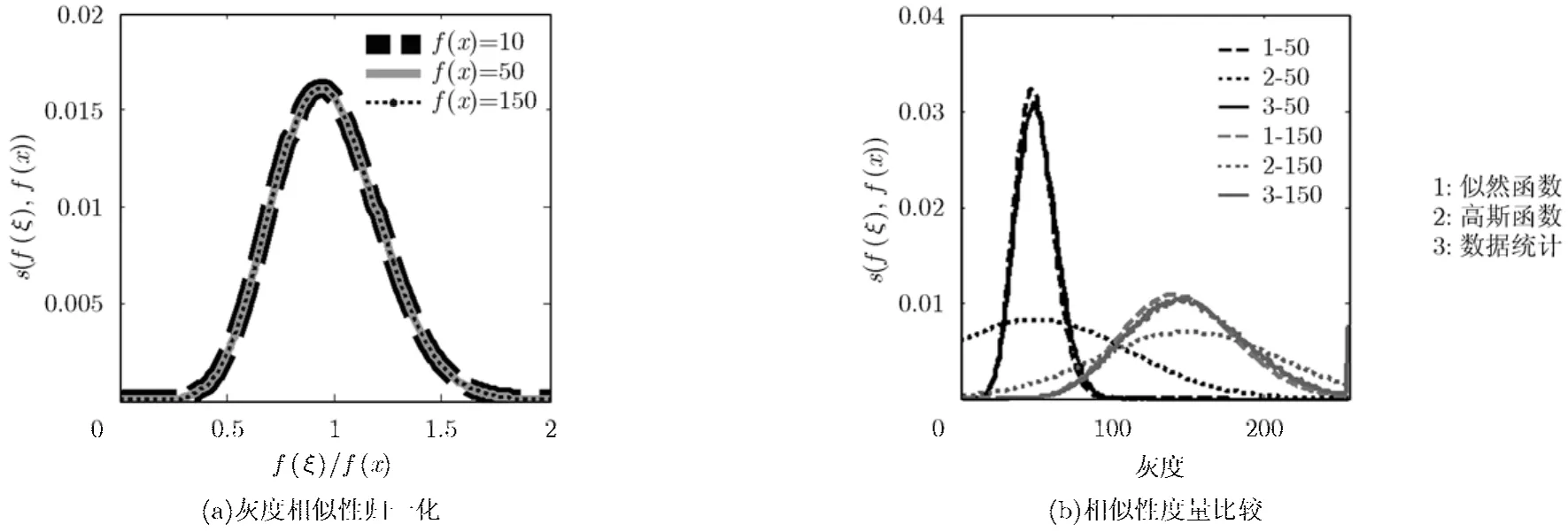
图2 似然函数进行灰度相似性度量结果

步骤3 计算局域变差系数CV，结合式(6)~式(8)确定σd与CV对应关系。

步骤4 执行滤波，逐像素窗口操作，得到像素估计值。

(1)根据式(6)，由CV(x)确定σd(x)；

(2)将σd(x)代入式(2)求得各像素空间相似性，由式(9)求得像素灰度相似性；

(3)将式(2)，式(9)计算结果代入式(1)，求得像素估计值。

步骤5 将步骤2~步骤4重复3~5次，得到最终滤波结果。

4 实验与结果分析

4.1 评价指标

在实验结果的评价方面，这里用以下两个指标进行评价：

(1)等效视数ENL反映图像的噪声平滑能力，在同质区域中，ENL越大，则相干斑抑制效果越好。设所选图像的同质区域为Ihom，则ENL计算公式为[10]

(2)在细节保持评价方面，这里引入一新指标：细节保持系数(Detail-Preservation Index,DPI)，计算如下：

其中D为图像的第3类区域，即满足CV≥Cmax的区域，f与h分别为滤波前后图像。DPI_M越接近1,DPI_V越小，则细节保持越好。

4.2 实验结果

为了验证提出方法的有效性，实验用3幅SAR图像作为测试图像：(1)图3(a)，仿真4视SAR图像；(2)图4(a)是Volgograd地区一幅6视TerraSAR-X幅度图像；(3)图5(a)，Flevol and地区的一幅4视AirSAR幅度图像，3个图像大小均为256×256。在实验中，本文方法分别与精致Lee滤波(RE_Lee)，文献[10]中的基本Bilateral滤波(BF)，基于NSCT局域高斯模型的MAP滤波[2](NSCT_GMAP)和基于NSCT双变量模型的滤波算法[3](SNSCTBI)进行了比较。在参数设置方面，本文选用5×5窗长迭代5次，比较算法各参数设置为：RE_Lee选用7×7的窗，BF选用11×11的窗，NSCT_GMAP与SNSCTBI均采用‘cd 9-7’小波5层分解，高频方向数均为[4 8 8 16]。各方法的滤波结果如图3~图5所示，滤波效果的评价如表1所示，各图(a)中矩形框区域为选定用于进行ENL计算的区域。

图3 仿真SAR图像滤波前后比较

观察图3中各方法的滤波结果可以看出：RE_Lee滤波相比BF的噪声平滑能力更强，但同质区域呈现出了具有一定方向性的斑块，这是由滤波过程中的方向计算不准确引起的；NSCT_GMAP滤波与SNSCTBI滤波相比RE_Lee滤波具有更强的噪声平滑能力，但边缘细节出现了模糊，且在同质区域呈现了明显的伪吉布斯效应；本文方法的同质区最平滑，边界清晰。表1对各滤波结果与真值间的均方误差(MMSE)进行了比较，结果显示本文方法的处理结果具有最小的均方误差值，这说明本文方法的滤波结果更接近于加噪声前的真实图像。

观察图4中各方法的滤波结果，尤其注意图像中部的一系列点目标，本文方法的滤波结果中目标清晰，而其它方法均有一定程度的模糊，这是由于本文方法具有自动调节窗口大小的能力，在变差系数大的区域窗长很小，可以起到细节保持的作用；观察图5的滤波结果可以发现，本文方法的滤波结果在接近区域交界线的地方，仍然具有很强的噪声平滑能力，这里因为本文方法可以根据像素的相关性对窗口内不同区域像素赋不同的权重，因此在接近区域交界线的地方仍然有尽可能多的同质区域像素起到噪声平滑的作用。

实验发现本文方法的滤波结果会存在一定的暗点或者暗斑，这是由于以当前像素作为真值来计算灰度相似性引起的，本文对滤波结果用简单的排序滤波器去最小值解决了该问题。

比较表1中的各项指标我们可以发现：相比其它方法，本文方法的滤波结果在同质区域具有最大的等效视数，且衡量细节保持的DPI_M更接近于1,DPI_V更接近于0；这一结果也证明本文方法在噪声平滑与细节保持上均优于其它同类算法。

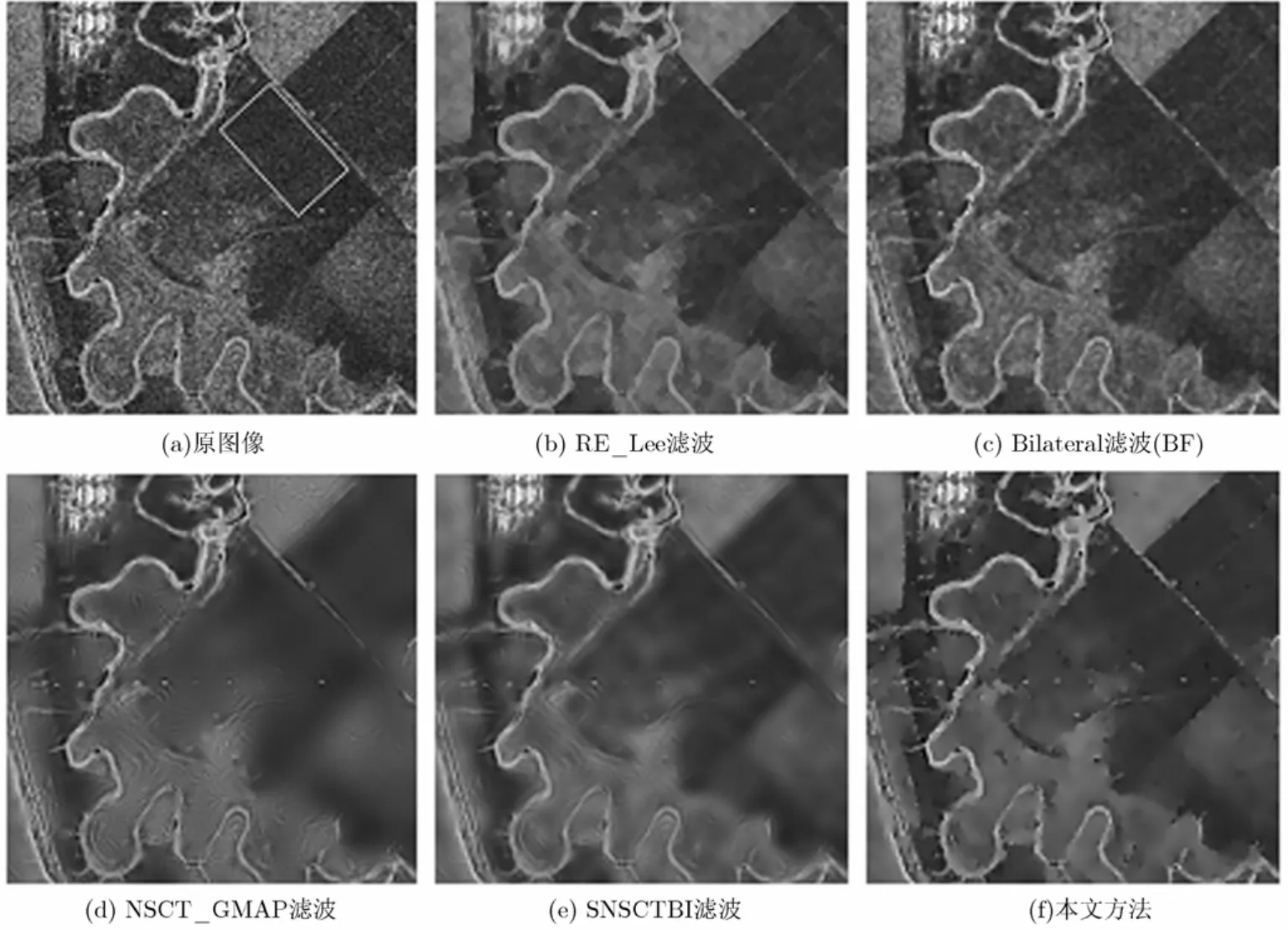
图4 Volgograd地区SAR图像滤波结果

图5 Flevoland地区SAR图像滤波结果

5 结论

SAR图像的相干斑抑制一直是SAR图像处理方面的研究热点。由于Bilateral滤波器在进行图像去噪时可以同时利用像素间的空间相似性与灰度相似性，近年来被引入到了SAR图像相干斑抑制中。分析发现，用Bilateral滤波器进行相干斑抑制时存在空间方差系数选择困难与灰度相似性模型不合理的问题，针对这两个问题，本文提出了一种自适应Bilateral滤波器。该方法根据SAR图像的局域变差系数来确定空间方差系数，从而调整高斯窗的形状，起到自适应调节窗长的作用；同时根据SAR图像的似然概率函数来度量窗内各像素与中心像素的灰度相似性，并根据相似性调节各像素的权重，起到方向选择的作用；从这个意义上讲，本文方法能够根据图像的结构信息自动调节滤波器的窗长与方向，是一种具有自适应能力的 SAR图像相干斑抑制算法。仿真与实测SAR图像的去斑实验表明，自适应Bilateral滤波器在去噪能力与细节保持方面均优于其它同类算法，是一种有效的相干斑抑制方法。

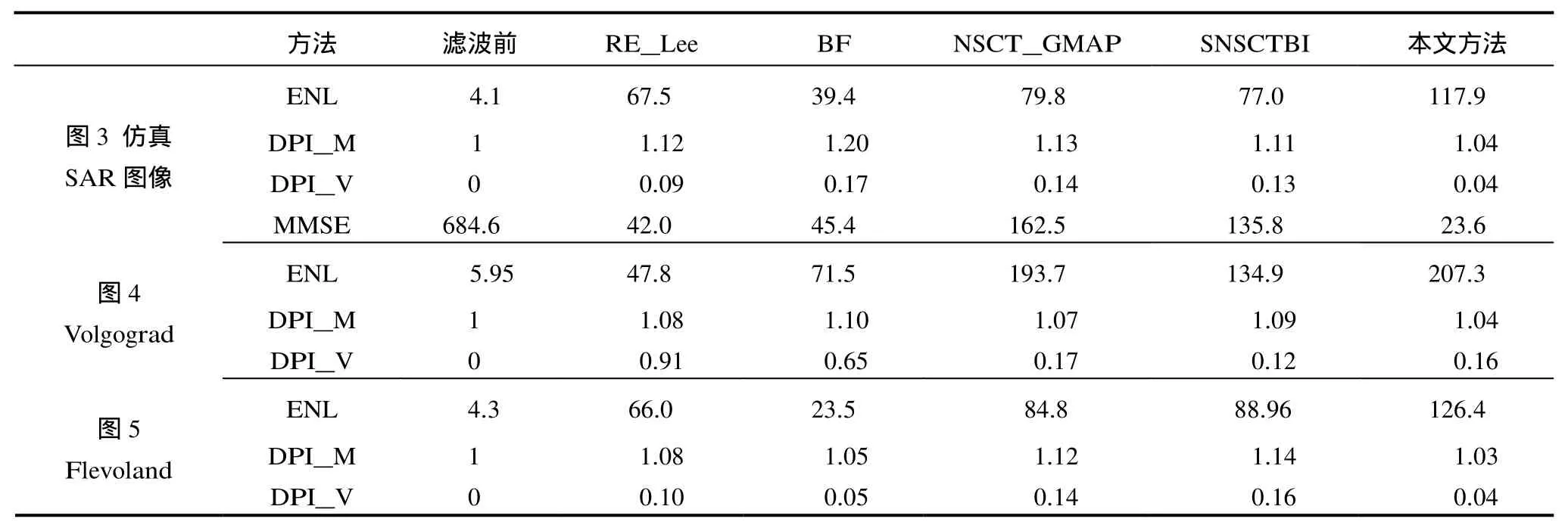
表1 滤波效果比较

[1]Amirmazlaghani M and Amindavar H.Two novel Bayesian multiscale approaches for speckle suppression in SAR images[J].IEEE Transactions on Geosciences and Remote Sensing,2010,48(7): 2980-2993.

[2]凤宏晓,侯彪,焦李成,等.基于非下采样 Contourlet域局部高斯模型和MAP的SAR图像相干斑抑制[J].电子学报,2010,38(4): 811-816.Feng Hong-xiao,Hou Biao,Jiao Li-cheng,et al..SAR image despeckling based on local Gaussian model and MAP in NSCT domain[J].Acta Electronica Sinica,2010,38(4):811-816.

[3]贾建,陈莉.基于双变量模型和非下采样 Contourlet变换的SAR图像相干斑抑制[J].电子与信息学报,2011,33(5):1088-1094.Jia Jian and Chen Li.SAR image despeckling based on bivariate threshold function in NSCT domain[J].Journal of Electronics＆Information Technology,2011,33(5):1088-1094.

[4]Tomasi C and Manduchi R.Bilateral filtering for grey and color images[C].Proceedings of IEEE International Conference on Computer Vision,New Delhi,India,1998:839-846.

[5]Barash D.A fundamental relationship between bilateral filtering,adaptive smoothing,and the nonlinear diffusion equation[J].IEEE Transactions on Pattern Analysis and Machine Intelligent,2002,24(6): 844-847.

[6]Elad M.On the origin of the bilateral filter and ways to improve it[J].IEEE Transactions on Image Processing,2002,11(10): 1141-1151.

[7]Han J W,Kim J H,Cheon S H,et al..A novel image interpolation method using the Bilateral filter[J].IEEE Transactions on Consumer Electronics,2010,56(1): 175-181.

[8]Lin C H,Tsai J S,and Chiu C T.Switching Bilateral filter with a texture/noise detector for universal noise removal[J].IEEE Transactions on Image Processing,2010,19(9):2307-2320.

[9]Zhang M and Gunturk B K.Multiresolution bilateral filtering for image denoising[J].IEEETransactions on Image Processing,2008,17(12): 2324-2333.

[10]Zhang W G,Liu F,and Jiao L C.SAR image despeckling via bilateral filtering[J].Electronics Letters,2009,45(15):781-783.

[11]Oliver C and Quegan S.Understanding Synthetic Aperture Radar Images[M].Boston.Artech House,1998: 75-120.

[12]Lopes A,Touzi R,and Nezry E.Adaptive speckle filters and scene heterogeneity[J].IEEE Transactions on Geosciences and Remote Sensing,1990,28(6): 992-1000.

[13]Molina D E,Gleich D,and Datcu M.Gibbs random field models for model-based despeckling of SAR images[J].IEEE Geoscience and Remote Sensing Letters,2010,7(1): 73-77.