状态空间法在超宽带雷达动目标速度及距离像估计中的应用
2012-09-19杨利民苏卫民耿润潼
杨利民 苏卫民 顾 红 耿润潼 邵 欣
(南京理工大学电子工程与光电技术学院 南京 210049)
1 引言
由于UWB雷达相对带宽2(f2-f1)/(f1+f2)不小于25%[1](f2和f1分别为超宽带信号频率的上、下限),通常而言该雷达具有高分辨距离像能力。与窄带雷达不同的是,常被看作“点”的目标对于UWB雷达而言其由多个散射体组成,因而具有更精细的距离像信息。然而,UWB雷达通过提高发射信号的绝对带宽(即f2-f1)以提高距离像分辨力的同时,存在相对径向运动的目标的多普勒频率由于较宽的绝对带宽而不再是点频,而是跟随信号频率变化,该现象称为多普勒色散(Doppler dispersion)[2]。这使得试图通过计算多普勒频率以获得径向速度变得困难。
根据文献[3,4],当多普勒色散因子BT(2v/c)<<1时(其中B,T分别为发射信号带宽和时宽,v和c分别为目标相对径向速度和光速),窄带回波模型仍适合,回波的伸缩可以忽略。然而,在 UWB雷达中,对于带宽B很宽及高速运动的目标,该因子极易接近或者大于 1。此时,回波存在与径向速度相关的伸长或者压缩,压缩因子s为(c-v)/(c+v)[3,4]。因此,需考虑多普勒色散对径向速度估计的影响。于是,文献[5]首次提出利用被美誉为“数学显微镜”的小波变换估计目标与雷达间距离及压缩因子s,再根据该因子获得相对径向速度,从而有效地规避了多普勒色散对径向速度估计的影响。
然而,利用小波变换时,限制了UWB雷达的发射波形,即发射波形需满足母小波容许性[5]。目前,有利用SS估计UWB雷达参数的相关研究[6-8],其考虑在高频区利用几何衍射理论(Geometrical Theory of Diffraction,GTD)建立带有散射体特征参数的散射体冲激响应模型,能获得高分辨距离及速度像。对于低速运动目标且多普勒色散因子远小于1时,GTD模型具有良好的适应性。然而,随着现代国防科技的飞跃发展,如X-37B无人太空战机等高速运动飞行器问世,探讨适应于高速运动目标的参数估计方法具有重要的应用价值。本文讨论当多普勒色散因子大于 1时,采用SS方法估计基于UWB雷达的目标径向速度及距离像。首先,当多普勒色散因子大于1时,结合具有伸缩的回波模型构造目标频域冲激响应。然后,利用SS法[9,10]估计目标高分辨距离像及压缩因子s,从而利用s进一步获得高精度径向速度。本文进一步推导了上述估计参数的 CRLB,并与通过蒙特卡罗(Monte Carlo,MC)重复试验获得的相应均方根误差(RMSE)进行比较,以分析估计参数的统计性能。SS法在低信噪比(SNR)下依然具有较好的估计性能,因此具有良好的噪声抑制能力。此外,由于只需要目标频域冲激响应而不涉及UWB雷达的具体发射波形,SS没有如小波变换对发射波形应具有容许性的限制[5]。
本文内容安排如下:首先,结合具有压缩的回波模型推导 UWB雷达下目标的频域冲激响应模型,并根据该模型获得Hankel矩阵;其次,讨论利用 SS估计存在径向运动的目标的距离及压缩因子s;然后,分别推导压缩因子s,距离R及初相位φ对应的CRLB;通过计算机仿真实验验证上述讨论;最后,总结全文。
2 UWB雷达目标频域冲激响应及状态空间模型
2.1 UWB雷达目标频域响应函数
为获得目标散射体的冲激响应函数,假设UWB雷达的发射信号fT(t)为狄拉克(Dirac)函数δ(t),则当UWB雷达BT(2v/c)>1时,根据文献[5]可得具有伸缩的回波模型:
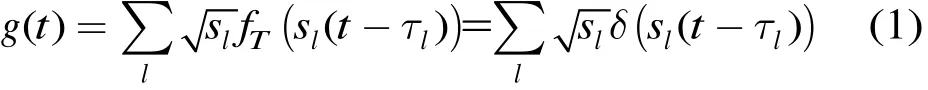
当第l个散射体的径向速度满足|vl|/c<<1,|·|为取模,则式(1)中第l个散射体压缩因子sl为
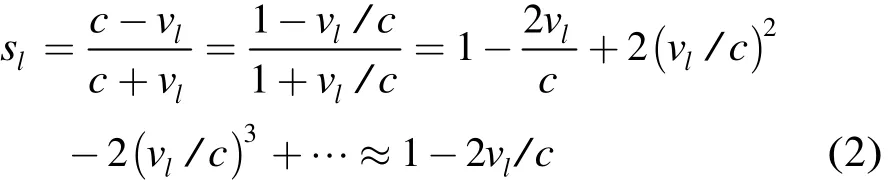
及其对应的时延τl为

其中Rl为第l个散射体与雷达间的斜距。对式(1)作快速傅里叶变换(FFT),即目标的频域冲激响应为
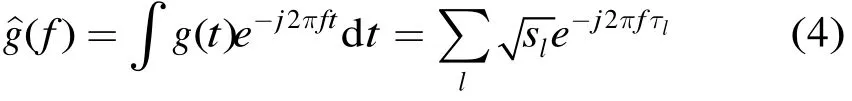
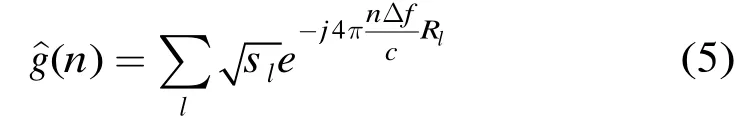
2.2 UWB雷达目标状态空间模型
对于线性系统,在控制理论中的不同于自回归滑动平均(Auto-Regressive and Moving Average,ARMA)的另一种常见模型为状态空间模型[10],即UWB雷达目标的离散状态空间方程可表示为[9]
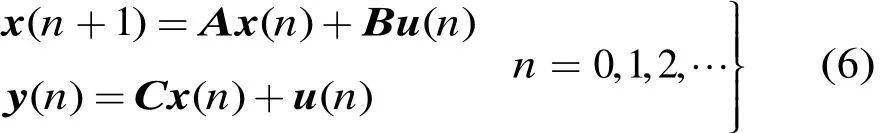
其中x(n)为其状态向量,且A为系统状态变化矩阵,B为输入量对状态影响矩阵,C为状态对输出影响矩阵。设该系统为1个输入和输出量,且状态变量个数为β,则有及C∈,ℂ表示复数集。由文献[10]可知,矩阵A的特征值对应ARMA模型的极值点;矩阵(A-BC)对应 ARMA模型的零值点。若该系统为零初始状态,输入为冲激函数,则有
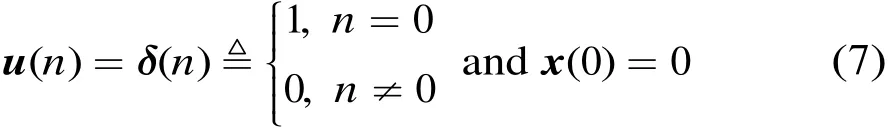
于是,根据式(6)可得冲激响应[6]:
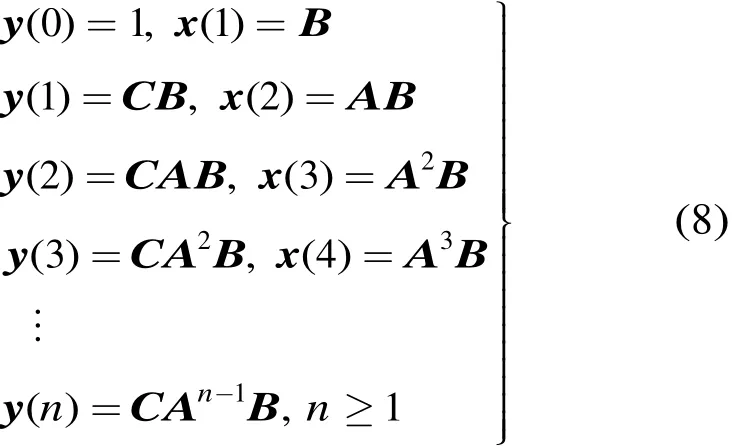
式(8)中y(n)=CAn-1B即为基于状态空间模型的冲激响应函数。
根据如式(5)所示的UWB雷达目标频域响应函数(n),其可进一步表示为
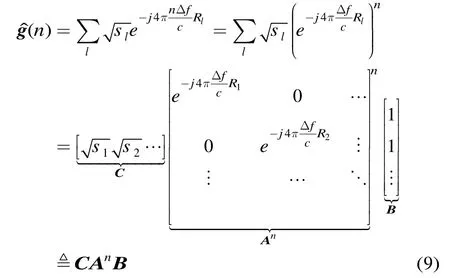
则结合式(8)中的第n个表达式和式(9),可得
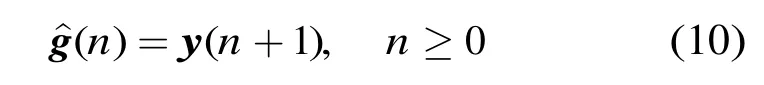
从式(10)可知,如式(8)的基于状态空间模型的冲激响应完全可以利用如式(5)所示的具有伸缩的回波模型的冲激响应函数(n)表示。于是,根据式(9)及Hankel矩阵的定义可构造Hankel矩阵H[9]为

其中N为回波采样个数,NR=round(2N/3)[6]为H矩阵的行数 (其中round(·)为取最近的整数)。
3 利用状态空间估计UWB雷达动目标距离及速度
由式(11),进行奇异分解(Singular Value Decomposition,SVD)可得[11]

其中∑=diag(σ1,σ2,…),且σ1≥σ2≥…,diag(·)为对角矩阵,(·)H为共轭转置(Hermitian)。由于对目标散射体个数估计的正确与否直接决定散射体距离及径向速度的估计精度及性能[12],因此需正确估计目标散射体个数。但传统的 AIC (Akaike Information Criterion)[13]和 MDL (Minimum Description Length)[14]在SS方法中存在如文献[15]所述的增加计算复杂度。于是,此处采用文献[6],即当∑中前m个对角线元素满足
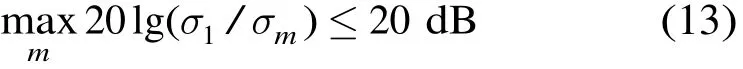
则认为目标由m个散射体组成。从而有
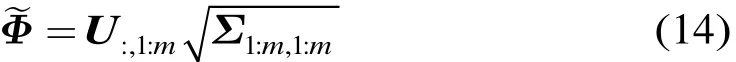
其中U:,1:m为矩阵U前m列组成的矩阵,∑1:m,1:m为矩阵∑前m个奇异值。若分别删除如式(14)所示矩阵的最后一行和第一行,可分别得到和+ ,即

由式(15)可得
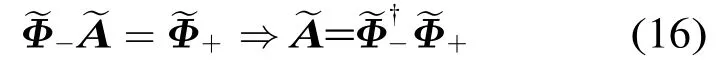
其中†表示伪逆(Moore-Penrose Pseudo-Inverse)[16]。则矩阵特征分解为

因此,由式(17)可得
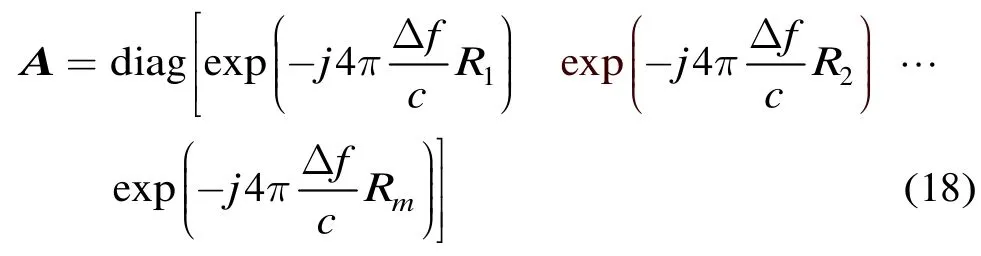
从而由式(18),各散射体到雷达间的距离可表示为
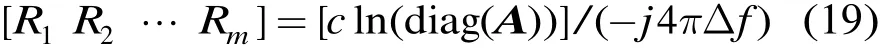
由式(9)及式(18)可得矩阵C,即

从式(2)及式(20)可得相应的目标径向速度
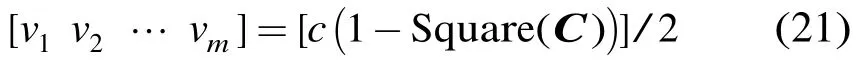
其中 Square(·)表示对(·)中各元素的平方。
4 距离/速度估计的CRLB
推导基于状态空间法的UWB雷达目标距离及速度的CRLB,以讨论SS参数估计的统计性能。由于2个及以上的散射体对CRLB的推导的复杂性,为了简化,本文只推导一个散射中心时的 CRLB。假设估计的参数为压缩因子,斜距和相位,表示为,则包含噪声的回波可表示为

其中y(n)为考虑噪声的回波信号,(n)为服从均值为0,协方差为σ2的加性高斯白噪声,即N(0,σ2),(n)为高斯白噪声(n)污染后的回波。(n)的概率密度函数可表示为
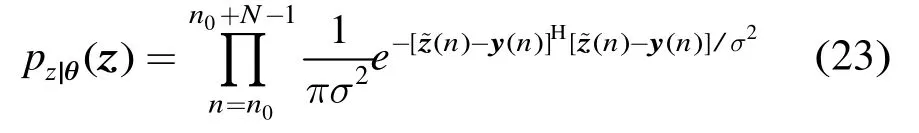
则由式(23)可得似然函数的对数形式

其中ln(·)为取对数。则由式(24)可得Fisher信息矩阵(FIM)的元素[6-7]:
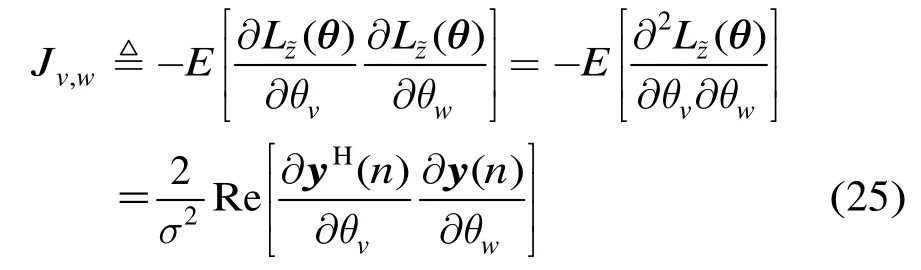
通过式(25),FIM可表示为
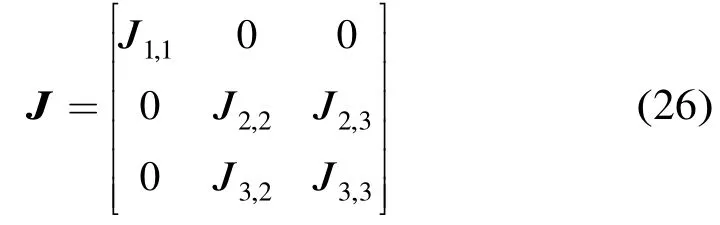
其中

根据式(26),对矩阵J求逆,可得矩阵CCR(θ)
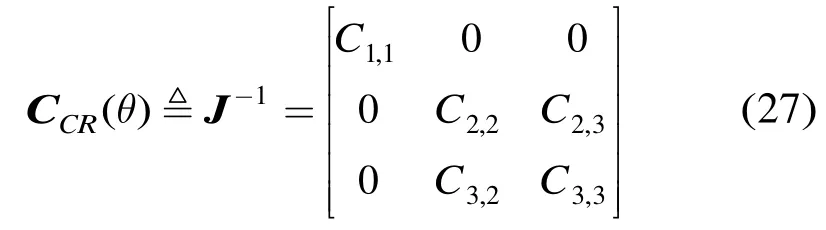
其中
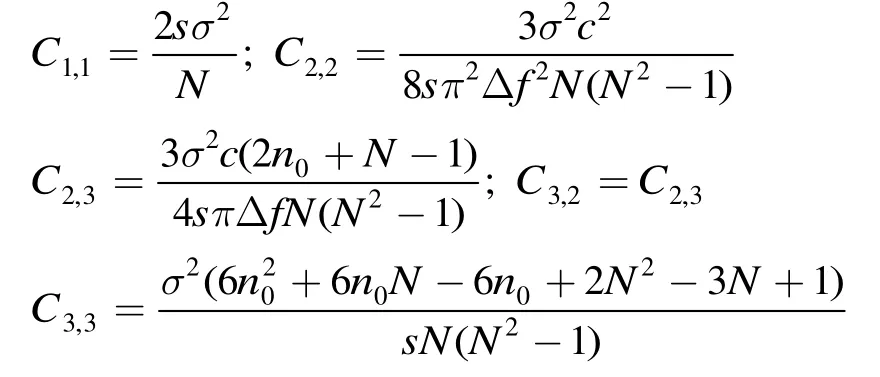
其中C1,1,C2,2和C3,3分别为θ(1,1),θ(1,2)和θ(1,3)(即压缩因子s,斜距R和相位φ)标准协方差的CRLB。
5 计算机仿真实验
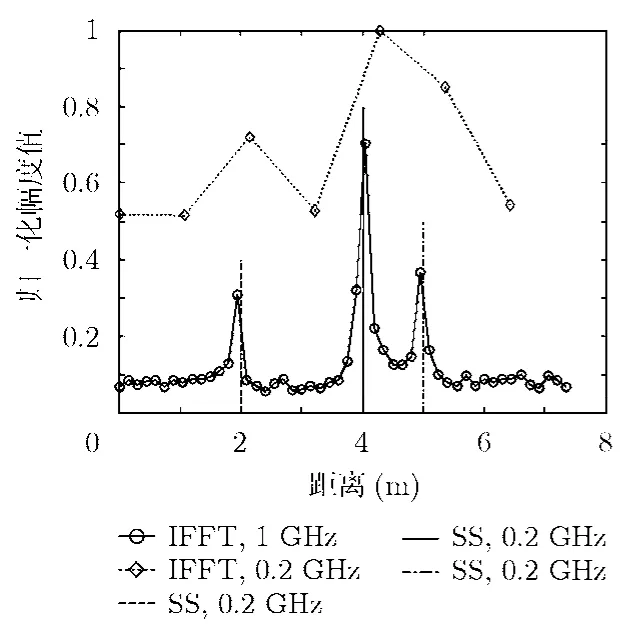
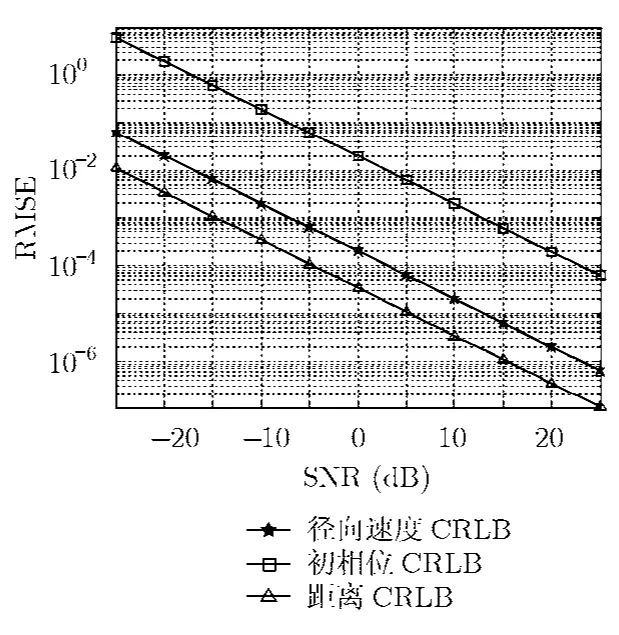
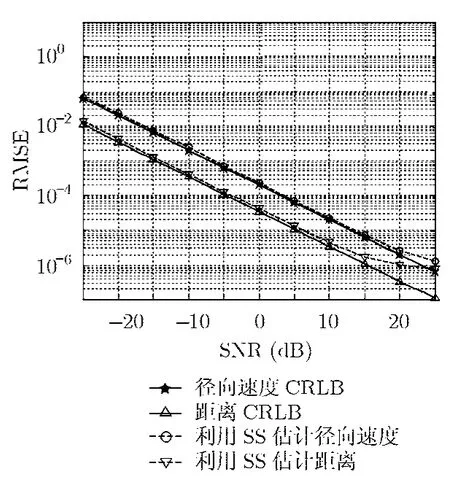
设目标由3个散射体组成,其和雷达间斜距分别为R0+2 m,R0+4 m和R0+5 m,其中R0=50 m。在本文中,由于最大不缠绕距离(即不模糊距离)Ru=c/ (2 Δf)=75 m,而目前所考虑的最大距离(R0+5) 现比较当UWB雷达发射信号带宽B分别为1 GHz和200 MHz时对如式(9)所示的频域冲激响应作逆傅里叶变换(IFFT)处理的目标距离像,以及当B为200 MHz时采取SS法估计的距离像。对上述获得的距离像如图1所示。 从图1发现,当利用IFFT时,在B为1 GHz能较好估计目标距离像。然而,当B为 200 MHz时,其估计性能大大降低,只能粗略反映其距离像轮廓。而采取SS法时,尽管B为200 MHz,仍能高分辨估计目标距离像。由此可知,在同带宽条件下,和IFFT相比,SS的距离像估计性能得到很大的改善。 为了讨论利用SS估计UWB雷达运动目标的径向速度,现假设4个平动刚体目标,其径向速度分别为6000 m/s,6500 m/s,7000 m/s和7500 m/s,且 UWB信号频率。雷达发射信号频率f∈[1,2]GHz,则对应带宽B为1 GHz,时宽T为0.5 ms,则这 4个运动目标中最小多普勒色散因子BT(2v/c)|v=6000m/s=20>1,所以其回波存在由因子s≈1-2v/c=0.99996决定的伸长,且该因子随着径向速度增大而降低。由SS获得的上述目标对应的压缩因子,然后结合式(2)计算出各自径向速度估计值及其对应的绝对误差如表1所示。 由表1发现,通过SS可以高精度估计UWB雷达径向速度。由图1和表1可知,通过SS法不但能高精度估计动目标径向速度,而且能获得高分辨距离像。而且,与小波变换估计中要求发射波形具有母小波容许性不同的是,由于SS只需目标冲激响应函数,而并未涉及具体的雷达发射波形,因此,本文采取的SS法没有对发射波形的严格限制。 表1 当SNR为20 dB时利用SS法获得不同径向速度的估计值比较(m/s) 由式(27)可得如图2所示的利用SS估计的目标径向速度、距离及相位随SNR变化的CRLB。 由图2可知,在低SNR情况下,利用SS估计的径向速度及距离也具有较低的CRLB值,从而使得高分辨估计目标的径向速度及距离像成为可能。 下面进一步对比估计参数的 RMSE及相应的CRLB,以分析参数的统计性能。设距离及径向速度估计参数的RMSE[17]定义为 其中L为散射体个数,(i)为第l个径向速度或者距离参数pl在共100次MC试验中第i次重复试验的估计值。当SNR从-25 dB到25 dB变化时,由式(28)估计的RMSE与对应的CRLB进行比较,以进一步分析利用 SS估计上述参数的性能,如图3所示。 从图3得知,随着SNR的增大,径向速度的估计精度也随着提高,在SNR小于15 dB时,与其CRLB很接近。尽管在SNR大于15 dB时其RMSE开始偏离CRLB,但由于RMSE保留在约 1 0-6量级,此时对径向速度精度影响可忽略。同样,利用 SS估计的目标距离像随着SNR增大,其估计精度显著改善,在SNR约20 dB处变化开始趋缓。由此发现,利用SS,不但能估计目标高分辨距离像,而且在对发射信号波形无限制及BT(2v/c)大于1的情况下,能估计高精度的径向速度。此外,当SNR较低时依然能保持较低的径向速度及距离像RMSE,因此,SS法在参数估计中具有良好的噪声抑制能力。 与窄带雷达不同的是,在UWB雷达中当高速运动目标的多普勒色散因子大于1时,其回波模型发生由相应压缩因子决定的伸缩。本文结合上述回波模型的特点构建目标频域冲激响应,采用SS分别估计目标的径向速度及距离像。然后,进一步推导了上述估计参数的 CRLB,并与通过蒙特卡罗重复实验获得相应的RMSE进行比较,以讨论估计参数的统计特性。由于SS法并未涉及具体UWB雷达发射波形形式,该方法对发射波形没有限制,这不同于小波变换。仿真结果表明SS不但能高精度估计运动目标径向速度,而且能获得高分辨距离像。通过比较参数估计值的RMSE及其CRLB可知SS估计的参数具有良好的统计性能。此外,SS法具有良好的噪声抑制能力。 图1 信号带宽B分别为1 GHz和200 MHz时利用IFFT及当B为200 MHz时利用SS估计的散射体(R0+2 m、R0+4 m和R0+5 m)距离像的比较 图2 利用SS估计径向速度、距离及相位的CRLB与SNR关系 图3 当随SNR变化时,利用SS估计目标距离及径向速度作100次MC试验的RMSE分别与其相应CRLB的比较 [1]Viet T V,Sjogren T K,and Pettersson M I.Ultrawideband chirp scaling algorithm[J].IEEE Geoscience and Remote Sensing Letters,2010,7(2): 281-285. [2]杨利民,苏卫民,顾红.基于脉组间频率步进的合成超宽带距离像及速度分析[J].航空学报,2010,31(10): 2046-2055.Yang Li-min,Su Wei-min,and Gu-hong.Analysis of synthetical ultra-wideband range profile and velocity based on stepped frequency during pulse trains[J].Acta Aeronautica et Astronautica Sinica,2010,31(10): 2046-2055. [3]Dixon T L and Sibul L H.Wideband imaging and parameter estimation of distributed objects using the continuous wavelet transform[J].Signal Processing,1996,54(3): 207-223. [4]Remley W R.Doppler dispersion effects in matched filter detection and resolution[J].Proceedings of the IEEE,1966,54(1): 33-38. [5]Weiss L G.Wavelets and wideband correlation processing[J].IEEE Signal Processing Magazine,1994,11(1): 13-32. [6]David J H.State-space approaches to ultra-wideband Doppler processing[D].[Ph.D.dissertation],Worcester Polytechnic Institute,2007. [7]Wang Jun,Wei Shao ming,Sun Jin ping,et al..A GTD model and state space approach based method for extracting the UWB scattering center of moving target[J].Science China Information Sciences,2011,54(1): 182-196. [8]王剑,吴嗣亮,侯舒娟.超宽带条件下运动目标的高分辨分析方法[J].电子与信息学报,2007,29(9): 2090-2093.Wang Jian,Wu Si-liang,and Hou Shu-juan.A high-resolution method for motive target in UWB[J].Journal of Electronics&Information Technology,2007,29(9): 2090-2093. [9]Rao B D and Arun K S.Model based processing of signals: a state space approach[J].Proceedings of the IEEE,1992,80(2):283-309. [10]Piou J E,Cuomo K M,and Mayhan J T.A state-space technique for ultrawide-bandwidth coherent processing.[Technical Report 1054].MIT Lincoln Laboratory,July,1999. [11]Foster J A,McWhirter J G,Davies M R,et al..An algorithm for calculating the QR and singular value decompositions of polynomial matrices[J].IEEE Transactions on Signal Processing,2010,58(3): 1263-1274. [12]Gulden P,Vossiek M,Storck E,et al..Application of state space frequency estimation techniques to radar systems[C].IEEE International Conference on Acoustics,Speech,and Signal Processing,in Salt Lake City,Utah,USA,2001,5:2877-2880. [13]Austin C D,Moses R L,Ash J N,et al..On the relation between sparse reconstruction and parameter estimation with model order selection[J].IEEE Journal of Selected Topics in Signal Processing,2010,4(3): 560-570. [14]Haddadi F,Malek-Mohammadi M,Nayebi M M,et al..Statistical performance analysis of MDL source enumeration in array processing[J].IEEE Transactions on Signal Processing,2010,58(1): 452-457. [15]王剑,吴嗣亮,侯淑娟.超分辨条件下雷达目标散射点数的估计方法[J].电子学报,2008,36(6): 1058-1062.Wang Jian,Wu Si-liang,and Hou Shu-juan.Detecting the scatterer number of radar target for SSM super resolution[J].Acta Electronica Sinica,2008,36(6): 1058-1062. [16]Hoyle D C.Accuracy of pseudo-inverse covariance learning—a random matrix theory analysis[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2011,33(7):1470-1481. [17]Zhang J,Dai J,and Ye Z.An extended TOPS algorithm based on incoherent signal subspace method[J].Signal Processing,2010,90(12): 3317-3324.
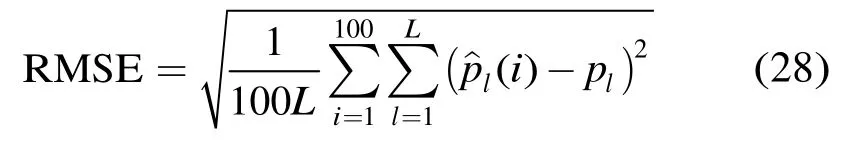
6 结论