调频步进频雷达中距离起点误差分析
2012-09-19田卫明
孙 林 田卫明 曾 涛
①(北京理工大学雷达技术研究所 北京 100081)
②(清华大学电子工程系 北京 100084)
1 引言
随着雷达技术的进步和微波遥感应用的扩展,军事侦察、地形测绘和微波遥感等领域对合成孔径雷达分辨率要求越来越高。分辨率改善需要提高雷达信号带宽,传统雷达信号的产生一般采用直接数字频率合成(DDS)技术直接产生宽带信号的方式。直接产生宽带信号的方法由于DDS工作时钟频率约束而受到限制。目前先进的超宽带雷达的信号带宽可达到GHz量级,而DDS技术难以在满足超宽带的同时保证信号质量。此外瞬时超宽带信号对AD采样速率和存储带宽也提出了较高要求。调频步进频信号是解决该问题的有效途径,因此在高分辨雷达系统中获得了广泛应用,如德国的PAMIR[1,2],法国的RAMSES雷达系统等都采用了调频步进频信号作为工作信号。
调频步进频体制在不增加瞬时带宽的条件下提高了雷达的距离向分辨率,同时降低了雷达系统对采样率的要求[3-6]。但是,调频步进频信号在脉冲压缩处理后通常会出现栅瓣[7]。文献[8,9]从模糊函数的角度分析了栅瓣出现的原因,提出了一种将栅瓣压低到阈值高度以下的方法,并从压低栅瓣的角度给出了调频步进频信号参数设计的建议。李海滨等人[10]提出了对调频步进频信号进行非线性压缩处理从而达到压低旁瓣和栅瓣的目的,同时保证了主瓣的展宽较小。通过分析发现,在时域合成算法中,由于算法的自身特点,当距离采样起点存在误差时也会引入栅瓣。
文献[11]推导的时域合成算法包括4个主要步骤:时移、频移、相位补偿、相干叠加。其中,在时域进行频谱搬移时,需要根据起始采样时间和采样频率来构造线性相位因子。在实际雷达系统中,标定误差会使实际起始采样时间与标称值存在误差,该误差会在宽带合成信号中引入阶梯相位,使宽带合成信号脉冲压缩后出现栅瓣。
本文首先简要概述调频步进频的时域合成算法,建立了距离采样起点的常数误差模型,推导了该误差与宽带合成信号中阶梯相位误差的关系,从线性系统单位冲激响应的角度分析了距离起点误差对栅瓣的包络、高度、分布情况以及主瓣偏移的影响进行了定量分析,最后给出了仿真结果和实测数据结果。
2 信号模型和宽带合成方法
调频步进频雷达通过脉内调频,脉间频率步进的方式扩展雷达带宽,脉内调频一般采用线性调频方式。采用线性调频步进频体制的发射信号为
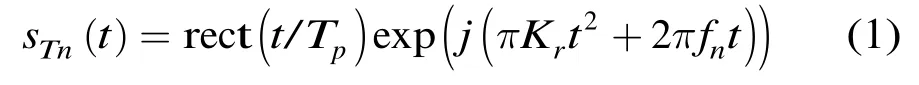
式(1)中,Kr为调频斜率,Tp为脉冲宽度,子带带宽为B=KrTp,fn为子带信号中心频率。设步进频雷达的载波中心频率为fc,频率步进点数为N,则fn可以表示为
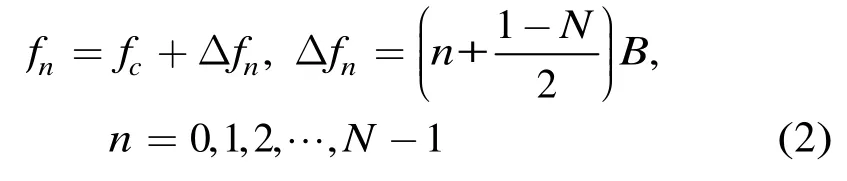
Δfn表示子带中心频率相对于宽带信号中心频率的偏移量。
调频步进频雷达一般采用高重频信号,此时一个脉组周期“stop and go”假设仍然成立,即各子脉冲回波延时近似相同,设为τ,则解调后的基带回波信号为

发射信号和解调后的基带信号如图1所示。

图1 调频步进信号
调频步进频雷达的回波信号首先进行带宽合成处理,一般采用时域带宽合成方法[12]。在时域带宽合成算法的处理流程如图2所示。
在调频步进频雷达系统中,子带信号的采样率通常小于宽带信号的带宽,因此在宽带合成前需要进行升采样,以保证进行频移时各子带信号的频谱不会混叠。由于子脉冲的采样窗长度通常小于宽带信号脉宽,因此在宽带合成前需要进行时域补零,以保证时移时子脉冲不会重叠。
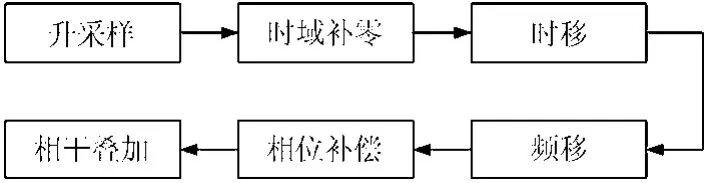
图2 时域合成算法处理流程
3 距离起点误差分析
3.1 误差形式
在实际系统中,产生发射和采样触发信号的频率源的实际值与标称值会存在误差,因此两触发信号的延时量,即实际起始采样时间与设计值会存在误差。由时间和距离的对应关系R=cτ/2,那么距离采样起点的实际值与设计值会存在误差。设距离起点设计值为Rideal,实际真值为Rmin,两者之差即为距离起点误差在时域合成算法中,频移处理通常是将子带信号在时域乘以线性相位因子exp(j2πΔfnt)完成,对于数字信号处理而言,需要构造时间轴。时间轴是利用起始采样时间和采样率来构造的。因此距离起点误差会造成时域合成算法中时域补零后构造的时间轴与实际时间轴tax存在误差,该时间误差为Δtax=2ΔRax/c,即=tax+Δtax。那么频移时与子带信号相乘的线性相位因子变为exp(j2πΔfntax)exp(j2πΔfnΔtax),即时间轴误差会在各子带信号中引入相位误差2πΔfnΔtax,设为Δφn。由式(2),Δfn为线性步进的,因此Δφn为阶梯形的相位误差。经过拼接处理后的宽带信号x(t)与理想宽带信号s(t)的频谱关系为
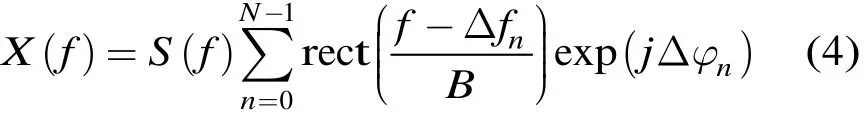
式(4)中的求和项即为距离起点误差在宽带拼接过程中引入的阶梯相位误差,设
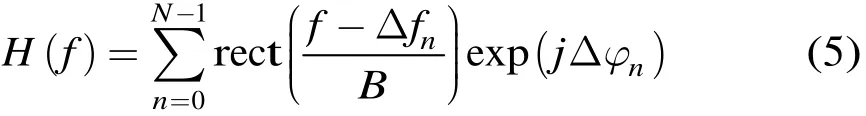
则X(f)=S(f)H(f),即距离起点误差引入的阶梯相位对宽带合成信号的影响等价于将理想宽带信号通过频率响应为H(f)的线性系统,该线性系统的单位冲激响应为
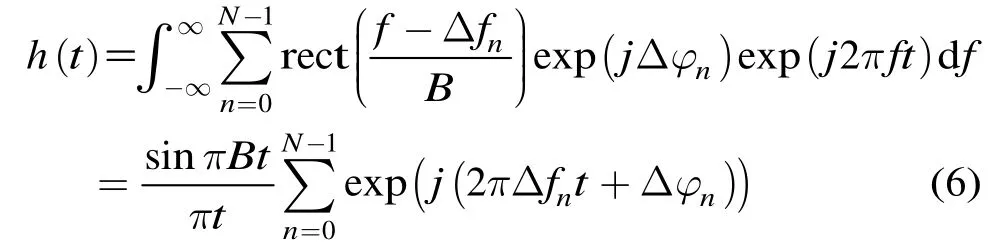
式(6)中各信号分量的初相为距离起点误差引入的阶梯相位,频率为子带信号中心频率相对于宽带信号中心频率的偏移量。由式(2)中Δfn的定义可知,式(6)为一组谐波分量之和,包络为sinc函数。对h(t)取模可得
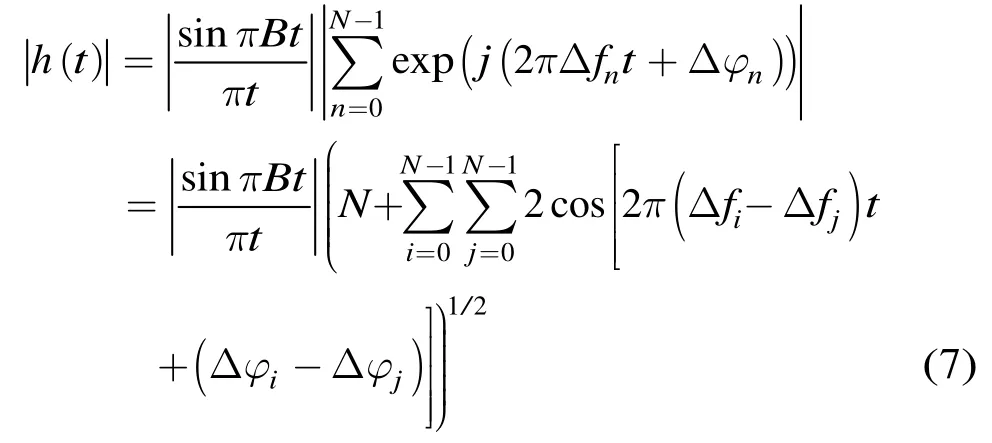
式(7)中余弦分量的频率为Δfi-Δfj=(i-j)B,故复指数信号和式模的最小正周期为Tsum=1/B。由sinc包络的零点位置为tzero=k/B,k为非零整数,即sinc包络除去第1零点外,其余相邻零点的距离为1/B。的形状如图3所示。
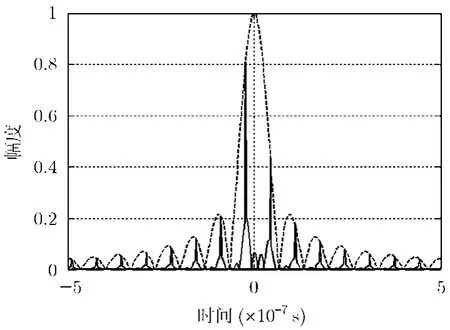
图3 单位冲激响应幅度
从图3中可以看到,单位冲激响应的模应存在很多周期性的尖峰,尖峰的包络为sinc函数。由于尖峰的间隔与sinc包络零点的间隔相等,因此当某一尖峰与sinc包络的峰值点重合时,其余尖峰与sinc包络的零点重合,此时单位冲激响应h(t)中只有一个尖峰。其余情况下单位冲激响应中会有周期重复的尖峰。
3.2 栅瓣产生
通过时域合成算法得到宽带信号x(t)后需要进行脉冲压缩处理。由卷积的性质可知,带有相位误差的宽带合成信号脉冲压缩后的结果,等价于理想宽带信号的脉冲压缩结果通过了单位冲激响应为式(6)的线性系统。由于该单位冲激响应包含了周期性的尖峰,因此脉冲压缩结果会出现栅瓣,栅瓣间的距离为1/B,即子带信号带宽的倒数,主瓣和栅瓣具有sinc形状的包络。
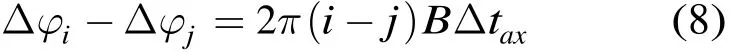
即初相为时间误差Δtax的函数。当时间误差变化时,周期性尖峰相对于sinc包络移动,因此栅瓣的位置和高度随Δtax变化。相位的周期为2π,各初相为2π整数倍的最小正周期为Tax=1/B,即栅瓣位置和高度随时间误差Δtax变化的周期为子带带宽的倒数。当时间误差为该周期的一半,即1/2B时,周期性尖峰关于sinc包络的峰值点对称分布,此时宽带合成信号脉冲压缩后会出现两个高度一样的主峰,即第1栅瓣的高度和主瓣高度相同。
3.3 主瓣偏移
将阶梯相位Δφn代入式(5)可得
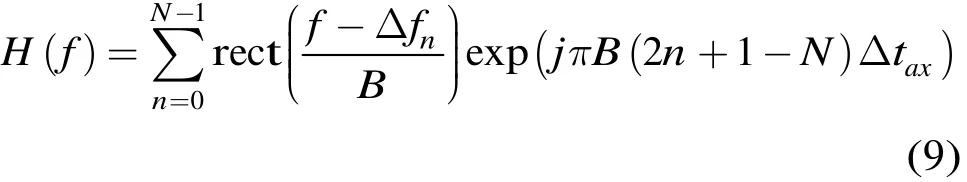
由于当步进点数N为奇数和偶数时,相位的分布情况不同。对当N为偶数的情况加常数相位偏移量,以便将两种情况下的相位分布情况统一:
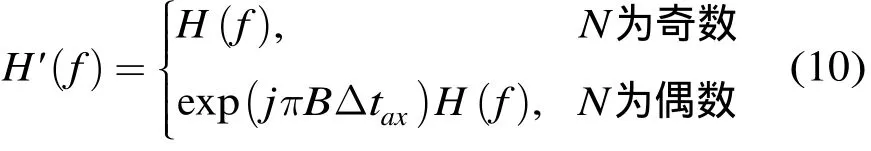
偏移处理后子带信号相位中的最小正值均为Δφmin=2πBΔtax。设该相位对主值区间[-π,π)取模后的结果为即为Δtax对[-1/B,1/B)的主值区间取模的结果,并设模糊数为k。对其余相位做类似的去模糊处理,并保证相邻相位的差在[-π,π)之间,则去模糊后的阶梯相位变为该相位中包含的一阶线性分量的斜率为
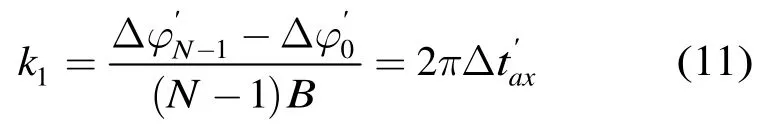
由傅里叶变换的性质,频域的线性相位会导致时域信号的移位,即单位冲激响应h(t)中的主峰相对于sinc包络的峰值点存在移位,偏移量为-,那么宽带合成信号脉冲压缩后的主瓣相对于sinc包络峰值点的偏移量即为-。
设理想宽带信号脉冲压缩后主瓣位置为tm,则实际合成宽带信号脉冲压缩后主瓣位置为
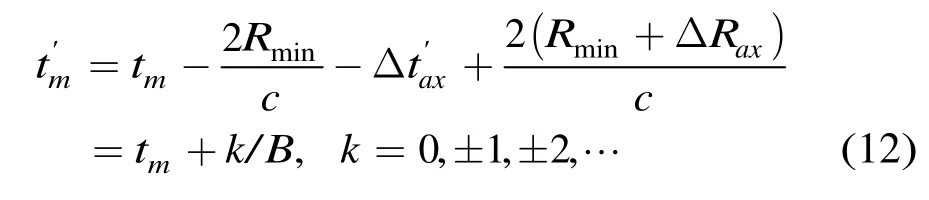
主瓣的位置的偏移会引入测距误差,误差大小为eR=kc/2B,即测距误差恰为子带信号分辨单元的整数倍。
3.4 栅瓣高度
由-π≤Δ<π,则-1/2B≤<-1/2B,栅瓣和主瓣的距离为1/B,则第1栅瓣相对于sinc包络峰值点的偏移量为
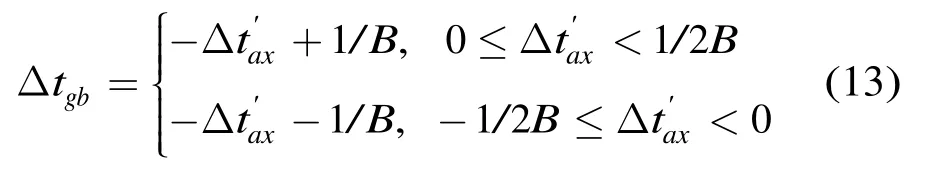
第1栅瓣与主瓣的相对高度为
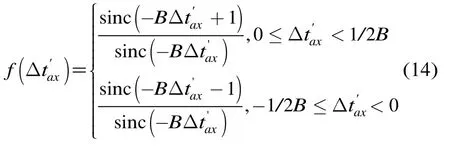
式中sinc函数的定义为sinc(θ)=sinπθ/πθ。化简后为
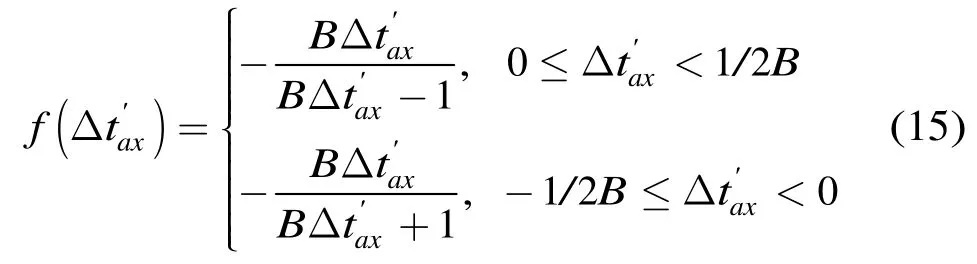
从图4中可以看到,第1栅瓣高度随着时间误差绝对值的增大而增大,当时间误差增大到±1/2B时,第1栅瓣高度和主瓣的高度相同,即出现两个主峰。当子带带宽增大时,栅瓣高度对时间误差更敏感,即相同的时间误差会导致更高的栅瓣。
4 仿真结果
下面对调频步进频时域宽带合成处理进行仿真,在各子脉冲中加入了常数距离起点误差,从而观察距离起点误差对栅瓣分布和对主瓣偏移的影响。系统仿真参数如表1所示。

表1 仿真参数
4.1 栅瓣包络和间隔
当引入时间误差为Δtax=5/fs=13.9ns时,宽带合成信号脉冲压缩处理后的结果如图5所示。
图5中第1栅瓣高度为-11.48dB,已经高于第1副瓣。虚线为sinc函数,可以看到栅瓣的包络确实为sinc形状,从而验证了式(6)的正确性。从图中可以得出栅瓣间的间隔为66.39ns,而子带带宽的倒数为66.67ns,误差小于一个采样间隔2.78ns。因此验证了栅瓣间隔为子带带宽的倒数这一结论的正确性。
当引入时间误差为Δtax=1/2B=33.3ns时,宽带合成信号脉冲压缩后的结果如图6所示。
从图6中可以看到,栅瓣的包络为sinc形状。此时有两个高度相同的主峰,即第1栅瓣的高度和主瓣相同,此时栅瓣性能最差,对成像结果的影响也最严重。因此,在实际系统中应避免时间误差为(2k+1)/2B(k为整数),对应的距离起点误差为(2k+1)c/4B,即半个子带信号分辨单元的奇数倍。
4.2 栅瓣高度和位置
下面改变时间误差Δtax,观察第1栅瓣高度、主瓣位置、栅瓣位置随时间误差的变化规律。其中,第1栅瓣随时间误差的变化情况如图7所示。
从图7可以看到,第1栅瓣的高度随时间误差Δtax是周期变化的,周期为66.67ns,即1/B。当时间误差为k/B时(k为整数),没有栅瓣;当时间误差为(2k+1)/2B时,栅瓣和主瓣高度相同。
主瓣位置和第1栅瓣位置随时间误差的变化情况如图8所示。
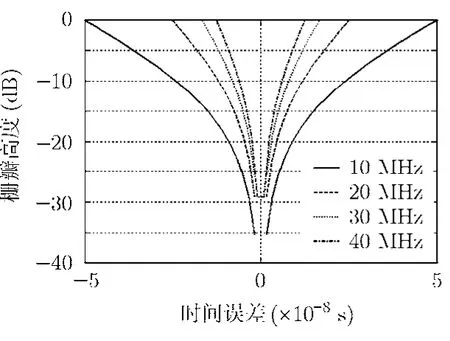
图4 第1栅瓣高度随时间误差的变化
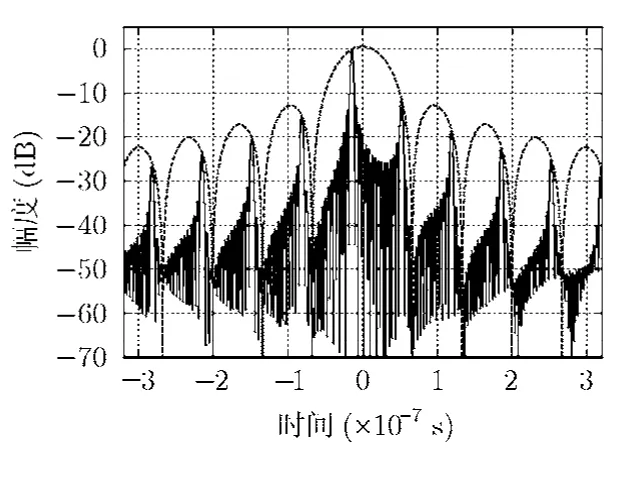
图5 Δtax=1 3.9 ns 时的栅瓣分布
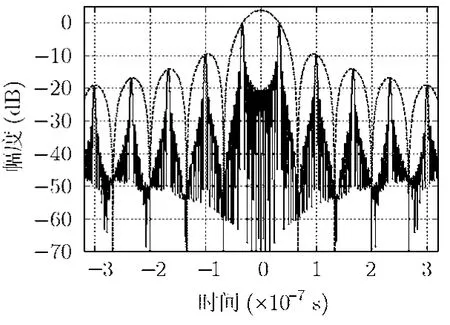
图6 Δ t ax=3 3.3 ns 时的栅瓣分布
图8中实线为主瓣位置,虚线为第1栅瓣位置。可以看到,主瓣位置随时间误差是单调增加的,时间误差的绝对值越大,主瓣位置的偏移量越大,即测距误差越大。主瓣位置曲线为阶梯形,阶梯的高度为1/B,因此主瓣的时间偏移量为k/B(k为整数),对应的距离偏移量为kc/2B,这与前文的结论是吻合的。主瓣和栅瓣位置的距离始终为1/B,只是主瓣和栅瓣的相对位置有所变化,第1栅瓣交替出现在主瓣的左右侧。这可以看成是随着时间误差的增加,第1栅瓣的高度也逐渐增加,当时间误差为(2k+1)/2B时,第1栅瓣的高度与主瓣相同,当时间误差再增加时,第1栅瓣的高度超过主瓣,从而栅瓣成为了主瓣,主瓣变为了栅瓣,主瓣和栅瓣的位置互换。
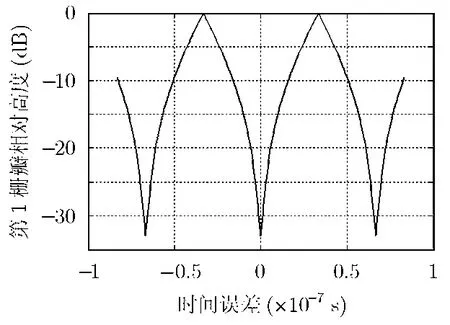
图7 第1栅瓣高度
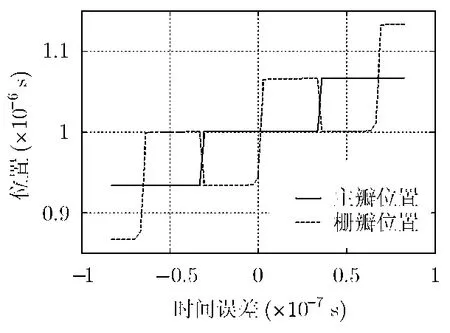
图8 主瓣位置和栅瓣位置
5 实测数据结果
下面对一组实测数据进行宽带合成和脉冲压缩处理。实验系统的参数如表2所示。

表2 实验系统参数
宽带合成信号的脉冲压缩结果如图9所示。图中虚线为利用系统给定的距离起点参数进行宽带合成和脉冲压缩处理后的结果,可以看到宽带合成信号的脉冲压缩结果中存在明显的栅瓣,栅瓣间隔为子带带宽的倒数。第1栅瓣的高度为-2.62dB,这会在最终的成像结果中引入大量的虚假目标,严重影响成像质量。
由于栅瓣的出现是由距离起点误差导致的,因此可以通过修正距离起点来减小距离起点误差导致的阶梯相位,从而降低栅瓣,减小误差的影响。通过迭代修正值,可以获得栅瓣最低的1维像,如图9中的实线所示,在修正后的脉冲压缩结果中,几乎看不到栅瓣。时间修正量为36.67 ns,大于1/2B,因此会导致主瓣位置的偏移,时间偏移量为1/B,对应的距离偏移量为10 m。比较图中距离起点修正前后的主瓣位置,修正前的主瓣位置为2478.8 m,修正后的主瓣位置为2488.8 m,主瓣偏移量为10 m,与理论推导相吻合。因此,实测数据验证了主瓣偏移结论的正确性。对比实测数据指出:距离起点修正前后的脉冲压缩结果说明通过对距离起点的修正可以极大地压低栅瓣,从而使栅瓣水平满足成像要求。
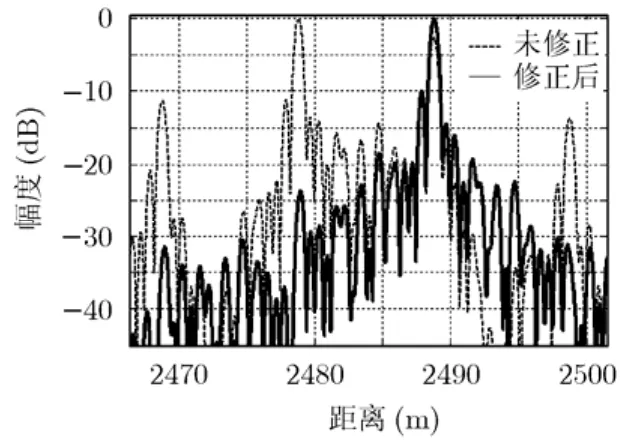
图9 实测数据处理结果
6 结论
距离起点误差会在宽带合成信号中引入阶梯相位,从而导致脉冲压缩结果中出现栅瓣。通过分析发现,栅瓣是周期重复的,周期为子带带宽的倒数,栅瓣的包络为sinc形状。若发射的子带信号在频率上有重叠,则栅瓣重复周期为回波信号滤波后子带带宽的倒数,即频率步进值的倒数。通过分析,得到了第1栅瓣与主瓣的相对位置和相对高度。除了引入栅瓣,距离起点误差还会造成主瓣位置的偏移,导致测距误差,测距误差随距离起点误差单调增加,呈阶梯形变化。最后,通过仿真和实测数据的处理,验证了以上结论的正确性。
[1]Ender J H G and Brenner A R.PAMIR - a wideband phased array SAR/MTI system.IEE Proc.Radar,Sonar and Navigation,2003,150(3): 165-172.
[2]Cerutti-Maori D,Klare J,Burger W,et al..Wide area traffic monitoring with the PAMIR system.Geoscience and Remote Sensing Symposim,IGARSS 2007,Barcelona,2007:3567-3570.
[3]Nie Xin,Zhu Dai-yin,Mao Xin-hua,et al..The application of the principle of Chirp scaling in processing stepped Chirps in spotlight SAR.IEEE Geoscience and Remote Sensing Letters,2009,6(4): 860-864.
[4]Luo Ying,Zhang Qun,and Qiu Cheng-wei.Micro-Doppler effect analysis and feature extraction in ISAR imaging with stepped-frequency Chirp signals.IEEE Transactions on Geoscience and Remote Sensing,2010,48(4): 2087-2098.
[5]Zhu Feng and Zhang Qun.Reconstruction of moving target’s HRRP using sparse frequency-stepped Chirp signal.IEEE Sensors Journal,2011,11(10): 2327-2333.
[6]Deng Yun-kai,Zheng Hui-fang,and Wang R.Internal calibration for stepped-frequency Chirp SAR imaging.IEEE Geoscience and Remote Sensing Letters,2011,8(6):1105-1109.
[7]Levanon N and Monzeson E.Nullifying ACF grating lobes in stepped-frequency train of LFM pulses.IEEE Transactions on Aerospace and Electronic Systems,2003,39(2): 694-703.
[8]Gladkova I and Chebanov D.Grating lobes suppression in stepped-frequency pulse train.IEEE Transactions on Aerospace and Electronic Systems,2008,44(4): 1265-1274.
[9]Gladkova I.Analysis of stepped-frequency pulse train design.IEEE Transactions on Aerospace and Electronic Systems,2009,45(4): 1251-1269.
[10]李海滨,张云华.降低调频步进信号副瓣的方法研究.现代雷达,2006,28(4): 45-49.
[11]Lord R T and Inggs M R.High resolution SAR processing using stepped-frequencies.Proc.IEEE Geoscience Remote Sensing Symposim,IGARSS 1997,Singapore.August 1,1997:490-492.
[12]李海英.超宽带信号波形及其合成孔径雷达成像研究.[博士论文],中国科学院电子学研究所,2002.
