基于混合迭代滤波的SAR图像相干斑抑制

朱 磊 水鹏朗 程 冬

(西安电子科技大学雷达信号处理国家重点实验室 西安 710071)

1 引言

合成孔径雷达借助大量随机分布的散射体反射的雷达回波相干叠加成像，从而不可避免地在SAR图像中产生一种称为相干斑的乘性噪声。相干斑噪声的存在严重降低了 SAR图像的视觉质量，限制了特征提取、目标识别等后续解译处理技术的有效性[1]。因此，相干斑抑制对于改进SAR图像成像质量，提高后续解译处理效果都具有重要意义。

SAR图像抑斑滤波算法主要有3类：空域滤波、变换域滤波与偏微分扩散滤波。空域滤波算法以Lee滤波[2]等为代表，这类算法通过滑动窗口获得图像局部统计特性来完成滤波，能较好抑制图像同质区的相干斑噪声，且算法简单有效、实时性好，但传统空域滤波采用固定尺度窗，难以在平滑噪声和保护图像细节之间保持平衡。另外，传统空域滤波的改进算法[3]需在滤波前进行图像区域划分来提升算法性能，但含噪图像的精确区域划分本身就十分困难。变换域滤波算法以小波和Contourlet变换滤波算法[4-8]为代表，这类算法利用变换域的子带系数特征设计滤波策略，可有效抑制高频噪声，能较好地实现区域平滑和纹理保留的折中，但算法须进行空域与变换域的相互转换以及各子带的分解与重构，复杂度高、计算量大，同时容易造成图像细节丢失与伪吉布斯现象。扩散滤波算法以各向异性扩散滤波[9]及其改进算法[10,11]为代表，这类算法利用图像局部结构信息对扩散的方向与强度进行约束，从而在噪声抑制与边缘保护上均取得了较好的效果，但容易引起图像动态范围减小、细节模糊与抑斑不充分问题。因此，单纯依靠一种方法完成 SAR图像相干斑的充分抑制与边缘细节的有效保护，是非常困难的[1]。

为此，本文提出了一种混合迭代滤波新算法。算法的提出主要有如下几点考量：(1)Lee滤波在SAR图像同质区噪声平滑能力突出且对噪声具有选择性平滑功能，即在图像同质区加大平滑，而在边缘区域又能停止平滑，这种选择性平滑特性为采用其它方法去除Lee滤波抑斑图像边缘区域残留的噪声奠定了基础。(2)Lee滤波平滑去噪受窗的尺度影响很大，大尺度窗Lee滤波的噪声平滑效果显著，但边缘含噪带较宽，同时出现部分边缘模糊迹象；小尺度窗Lee滤波的噪声平滑能力明显下降，同质区孤立点噪声较多，但边缘保护较好，边缘含噪带不明显，因此，采用变尺度窗Lee滤波会得到比固定尺度窗更好的去噪与保边效果。(3)无论选择大尺度窗还是小尺度窗，仅仅进行单次Lee滤波，抑斑图像仍有不少噪声残留，其中又以孤立点噪声与边缘噪声最为明显，因此，单次Lee滤波去噪性能有限。(4)自蛇扩散[12,13]利用图像局部结构信息去噪，虽在同质区的噪声抑制能力不及Lee滤波，但却能有效去除图像中的孤立点噪声与边缘区域噪声，并伴有边缘增强作用。因此，如果将利用局部统计特性的 Lee滤波与利用局部结构信息的自蛇扩散结合，利用前者平滑图像同质区噪声，利用后者去除孤立点噪声与边缘噪声，并增强由于Lee滤波平滑而变到模糊的部分边缘，同时采用先Lee滤波后自蛇扩散的混合滤波策略，又能进一步利用Lee滤波对噪声的预先平滑而降低噪声对自蛇扩散的不利影响，使得图像所有区域噪声都将得到较好抑制，而且边缘模糊迹象还得以缓解。进而，如果将单次Lee滤波改进为迭代Lee滤波，则不仅便于同本身就是迭代运算的自蛇扩散进行混合，同时多次迭代滤波还能最大限度地平滑噪声。另外，为防止多次混合迭代出现对图像边缘与纹理的过平滑问题，在迭代时，先从小尺度窗开始，每迭代一次窗尺度逐渐增大，从而既保护了边缘又最大限度地抑制了噪声。

2 Lee滤波与自蛇扩散

2.1 Lee滤波

在空域，设单视幅度格式SAR图像(m,n)处像素的散射幅度为σ(m,n)，则其观测模型可表达为[14]

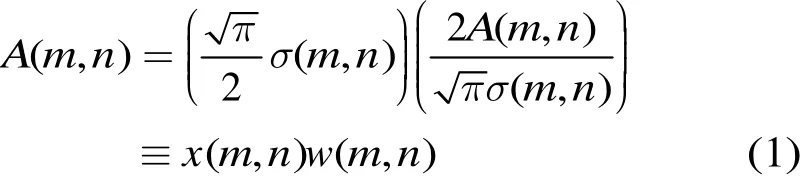
其中x为场景参数，是正比于各单元散射幅度的参量，w称作幅度格式下的乘性相干斑。Lee滤波这种基于局部统计特性的相干斑空域滤波算法，假设场景参数x为 2维分片常数且与相干斑噪声w独立，而噪声均值E(w)=1 ，方差。按此假设，Lee滤波可表示为

由式(2)与式(3)可知：Lee滤波场景参数x的滤波估计值实质是由场景参数在窗内的局部均值估计与场景实际观测值A的加权平均获得。当处于均匀场景时，场景参数x的局部方差D(x)较小，α≈ 0 ，这样场景参数的滤波估计值ˆx就由窗内像素的平均估计值决定；而当处于边缘等非均匀场景时，场景参数x的局部方差D(x)较大，α≈1，这样场景参数的滤波估计值xˆ就由场景观测值A决定，即场景参数的滤波估计值就保持原观测值不变，从而保护边缘不被平滑。Lee滤波这种选择性平滑的抑斑特点可从图1所示的仿真实验看出。图1(a)是128×128的原始卡通图像，对图1(a)中加入均值为1，方差为0.1的乘性噪声获得图1(b)，分别利用5×5和9×9的窗对图1(b)进行单次Lee滤波获得图1(c),1(d)。两幅抑斑图像清晰地显示：在卡通图像的均匀场景区域，噪声得到较大抑制，但边缘区域噪声却几乎没有变化，同时与小尺度窗Lee滤波获得的图1(c)相比，大尺度窗Lee滤波获得的图1(d)，同质区更平滑，孤立点噪声更少，但边缘噪声带也更宽，这说明固定尺度窗无论尺度大小均会对 Lee滤波抑斑产生不利影响。利用 5×5和 9×9的固定尺度窗与变尺度窗(初始窗从 4×4开始，每迭代一次窗尺度加倍)进行迭代 Lee滤波，可得图1(e)～1(g)。3幅抑斑图像的共同特点是：同质区噪声都得到更好的平滑。但选择小尺度固定窗的图1(e)，同质区噪声抑制没有图1(f)和图1(g)充分，而选择大尺度固定窗的图1(f)边缘含噪带又比图1(e)和图1(g)更宽，同时图像右上角部分边缘模糊迹象也更明显，3幅去噪图像中，只有迭代变窗Lee滤波获得的图1(g)，在同质区噪声抑制、边缘噪声带宽度与边缘保护程度三方面都表现出更好的性能。

2.2 自蛇扩散

若令图像的所有水平集按测地线活动轮廓模型运动，就产生了自蛇扩散这种非线性扩散滤波方法，用数学公式描述为

图1 不同参数Lee滤波与自蛇扩散的抑斑效果

其中图像观察值A的自蛇扩散由两部分组成，即扩散项与冲击项Fshock=，而函数g为带边缘检测的扩散控制函数。扩散项经局部坐标变换可得

其中x表示与图像边缘的切线方向一致的单位矢量，因此扩散项Fdiff实质为带有扩散控制函数g的方向扩散。而冲击项则是一种带有边缘增强作用的冲击滤波。由于扩散控制函数g利用A的梯度模作为边缘检测的依据，考虑到梯度参量对噪声的敏感性，在进行边缘检测前，需利用高斯平滑算子对图像作平滑处理。另外，g函数有多种形式，常见的一种为

其中K为反差参数。由于自蛇扩散中的方向扩散能沿图像边缘的切线方向进行，因此能在消除边缘噪声的同时而不引起边缘模糊，而冲击滤波则又能有效去除点噪声并增强大尺度对象的边缘锐度。但由于自蛇扩散仅仅进行沿边缘的方向扩散，而且迭代扩散运算仅在较小的邻域内进行，因而噪声平滑能力不足，同时自蛇扩散基于梯度模值来控制扩散进程，故受噪声影响大，自蛇扩散的这种抑斑特性可从图1所示的仿真实验看出。对单次Lee滤波抑斑图像图1(c)和图1(d)分别再利用自蛇扩散(仅迭代3次)进行去噪处理，获得图1(h),1(i)，与图1(c),1(d)相比，其同质区孤立点噪声大为减少，边缘噪声带也得到抑制，边缘也有锐化增强痕迹，但同质区平滑程度却没有明显改善。

从图1(c)～1(g)5幅去噪图像可以发现，利用变窗迭代Lee滤波获得的图1(g)，其图像同质区噪声抑制最充分，边缘噪声带最窄，边缘模糊程度也最小，但由于Lee滤波固有的选择性滤波特性，故变尺度窗虽可以减小抑斑图像的边缘噪声带宽度，但却不能从根本上消除边缘区域噪声。为此，在变窗迭代Lee滤波基础上，引入自蛇扩散用于去除Lee滤波难以去除的残留孤立点噪声与边缘噪声，从而在图像各区域都可取得较好的抑斑效果，同时 Lee滤波对含噪图像的预先平滑又可大大减弱噪声对自蛇扩散的不利影响，防止虚假边缘得到增强。图1(j)是由图1(b)经变窗Lee滤波与自蛇扩散通过3次混合迭代获得的抑斑图像，与其它抑斑图像相比，图1(j)不仅同质区噪声平滑更理想，而且有效克服了Lee滤波边缘噪声带处理困难的问题，同时自蛇扩散对图像边缘的增强作用，又使得由于Lee滤波多次迭代与窗尺度增大而引起的部分边缘模糊问题得以控制。

3 变窗Lee滤波与自蛇扩散的混合迭代滤波算法

混合迭代滤波算法在每次混合迭代中主要进行3步操作：先估计SAR图像局部统计量，接着基于局部统计量利用变窗Lee滤波进行平滑滤波，最后利用自蛇扩散去除Lee滤波抑斑图像中残余的孤立点噪声与边缘区域噪声，并锐化边缘。

3.1 SAR图像局部统计量估计

Lee滤波这种基于图像局部统计特性的空域滤波方法，在滤波前须先完成 SAR图像局部统计参量的估计，需估计的参量有：场景参数的局部均值与局部方差D(x)，噪声的全局方差。假设SAR图像相干斑噪声模型如式(1)所示，若采用r×r矩形窗R，则场景参数x的局部均值估计为

为估计场景参数x的局部方差D(x)，可先将式(1)的相干斑乘性模型转化为加性模型。

由于场景参数x与噪声w相互独立，故由式(8)容易推出

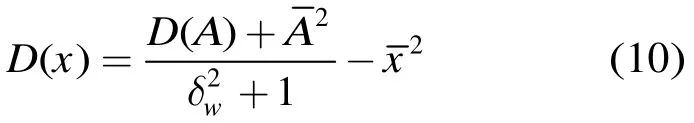
式(10)表明：D(x)的估计须先计算,,D(A)及，其中与由式(7)估计，而D(A)可由式(11)估计。

二是在 SAR图像中找出一块平坦区域，然后在选定区域按式(13)估计。

上述两种方法估计的噪声方差都是局域性的，不同图像区域的估计值差异明显，而 SAR图像真实噪声方差在整个图像范围内却是一常数值。为此，本文提出了一种简单有效的 SAR图像噪声方差估计方法，具体估计步骤是：先利用式(13)计算图像各像素点的局部噪声方差估计，然后利用直方图方法统计图像各像素点局部噪声方差估计值最集中的数据值，而这个数据值就是最终的全局噪声方差估计值。新方法的提出是基于一般 SAR图像的大部分区域均为同质区这一假设，并利用直方图统计方法巧妙地将图像边缘与复杂纹理区域中不准确的噪声方差估计值剔除，同时也避免了传统估计方法噪声方差的多值估计问题。

3.2 变窗Lee滤波

完成 SAR图像局部统计量估计之后，便可利用式(2)与式(3)进行Lee滤波了。与传统Lee滤波相比，本文算法对 Lee滤波进行了 3处改进：(1)将传统Lee滤波的固定窗，改为变尺度窗；(2)将传统单次运行Lee滤波改为迭代运行，且窗尺度随混合迭代次数的增加而加倍；(3)将传统Lee滤波所采用的式(3)改进为

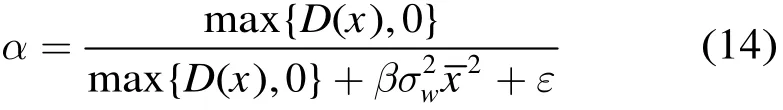
其中，利用max{D(x),0}取代D(x)是防止估计的方差D(x)＜ 0 ；参数ε是一取值很小的常数，其存在是为防止分母为零而造成α无穷大；参数β称为迭代倍乘因子，其存在是为了在每次迭代中提高对噪声的平滑程度，减少混合迭代次数。由于Lee滤波在同质区对噪声具有较强的平滑能力，随着混合迭代的进行，新估计的噪声方差会急剧减小，造成在同质区α≈1，从而使得场景参数的滤波估计值ˆx由场景观测值A决定，进而引起算法噪声平滑能力的显著下降，为了尽可能地抑制噪声，势必要增加混合迭代的次数。另一方面，混合迭代次数越多，Lee滤波的窗尺度也越大，而Lee滤波的窗尺度过大又会引起SAR图像局部统计参量估计偏差过大，失去局部统计意义，因此混合迭代次数又不能过多。为了尽可能地抑制噪声，同时减少混合迭代次数，提高运算速度，因此，在式(3)基础上引入参数β，用于在每次混合迭代中尽可能扩大噪声的抑制程度，一般SAR图像经过3～4次混合迭代就能达到较好去噪效果。β可通过式(15)计算确定。

其中num为最大混合迭代次数，τ为尺度因子，一般5 ≤τ≤ 2 0效果较好。

3.3 自蛇扩散滤波

含噪SAR图像利用改进的变窗Lee滤波完成初步抑斑后，就可利用式(4)进行自蛇扩散滤波，此时仅需要将式(4)中的A全部替换为经 Lee滤波去噪后的场景参数估计值xˆ，即

需要说明的是：式(16)的数值计算不能直接采用中心差分方案，而应采用迎风方案[13]。

混合迭代滤波算法先进行改进的变窗 Lee滤波，后进行自蛇扩散，这种组合抑斑策略，一方面可以利用自蛇扩散有效去除传统Lee滤波难于平滑的孤立点起伏与边缘噪声，另一方面，Lee滤波对图像噪声的预先抑制，不仅大大降低了噪声起伏对自蛇扩散的不利影响，同时也明显减少了自蛇扩散自身需要的迭代运算次数。对一般 SAR图像，混合迭代算法的迭代次数在2～4次之间（具体迭代次数可由估计的噪声方差阈值来决定），而在一次混合迭代中，自蛇扩散自身也仅需迭代2～4次。因此，混合迭代滤波算法的运算量远比扩散滤波与变换域滤波算法小，具有较好的实时性。

4 实验结果

为评估本文算法在 SAR图像相干斑抑制与边缘保护方面的性能，设计了两类实验，并与经典的Lee滤波[2]、增强 Lee滤波[3]、各项异性扩散滤波(SRAD)[9]以及非下采样 Contourlet变换滤波(NSCT)[7]进行了实验效果对比，其中采用的客观评价指标如下：

(1)等效视数(ENL)：用于反映图像的滤波效果，其表达式为

其中E和V分别为去噪图像均匀场景的均值和标准差，ENL值越大表明噪声抑制效果越好。

(2)比值图像的均值与方差(分别记为 PE与PV)：在理想情况下，原始图像与抑斑图像的比值即为斑点噪声图像，而比值图像的均值PE反映了抑斑算法对原始图像辐射特性的保持程度，理想值为1；比值图像的方差PV则反映了去噪算法对相干斑的抑制程度，与理想值越接近越好，对于幅度格式SAR图像其理想PV值为(4/π- 1)/L，其中L为视数。

实验 1 由于真实 SAR图像无法准确获得边缘等信息，为客观的展现不同算法的抑斑与边缘保护性能，本文构造出一幅256×256的卡通图像，如图2(a)所示，其真实边缘的二值图像如图2(b)所示。对图2(a)添加均值为1，方差为0.1的乘性斑点噪声，使其成为一幅6视幅度格式仿真SAR图像，如图2(c)所示，然后分别利用各抑斑算法对图2(c)进行抑斑，并对获取的抑斑图像进行边缘检测(采用阈值为0.08的Canny边缘检测算子)，实验结果如表1与图2所示。

图2 实验1中各算法对仿真SAR图像的抑斑效果

实验2 利用各去噪算法对图3(a)所示的8视幅度格式机场SAR图像(400×400)进行抑斑，并对获取的抑斑图像进行边缘检测(采用阈值为 0.1的Canny算子)，实验结果如表2与图3所示。在两类实验中，各算法主要参数如下：(1)Lee滤波与增强Lee滤波均采用9×9矩形窗；(2)SRAD扩散迭代运算150次，时间步长0.04; (3)NSCT算法采用3层分解，各层方向子带数为：8,8,16; (4)本文算法混合迭代3次，变窗Lee滤波初始窗大小为4×4，自蛇扩散在每次混合迭代中进行2次迭代运算，反差参数K=10。另外，ENL的计算区域分别为图2(a)与图3(a)中矩形虚线框选定的同质区，而PE与PV的计算区域则为整个图像。

表1 实验1中各算法对仿真SAR图像的抑斑效果参数对比

图3 实验2中各算法对真实SAR图像的抑斑效果

从实验1与实验2的抑斑对比实验可以发现：本文算法在ENL,PE及PV指标上均优于其它算法，而 ENL指标更是远远高于其它算法。从图2与图3的直接目视比较也能发现：本文算法获得的去噪图像(图2(h)，图3(g))同质区均比其它算法平滑，没有图2(d),2(e)和图3(c),3(d)中明显的孤立点噪声散布，没有图2(f)和图3(e)的边缘模糊现象，也不存在图2(g)和图3(f)中的虚假条纹。这说明从参数与目视效果对比来看，本文算法对图像各区域噪声的平滑能力都要优于其它算法。从图像边缘与重要场景目标的保护方面来看，本文算法获得的边缘检测结果(图2(m)和图3(l))与其它算法边缘检测结果(图2(i)～2(l)，图3(h)～3(k))相比，虚假边缘最少，重要场景目标(例如图3(a)中间的3架飞机、右下角的机场航站楼等)的轮廓均被清晰的保留，最接近图像的真实边缘。这说明本文算法在去噪的同时较好地保护了图像的边缘与重要场景目标。综上，在抑斑与边缘保护方面，本文算法对仿真 SAR图像与真实 SAR图像均取得了较好的效果，从目视效果与定量指标比较来看，均较其它算法理想。

表2 实验2中各算法对真实SAR图像的抑斑效果参数对比

5 结束语

将改进的变窗Lee滤波同自蛇扩散结合，利用变窗Lee滤波平滑同质区噪声，借助自蛇扩散去除Lee滤波难以去除的孤立点噪声与边缘区域噪声，而先Lee滤波去噪，再自蛇扩散的组合策略，使得Lee滤波对图像噪声的预先抑制，有效降低了噪声对自蛇扩散的不利影响，同时自蛇扩散沿边缘扩散与冲击滤波的边缘锐化增强作用又弥补了Lee滤波平滑噪声时对部分边缘的模糊问题。进而，两种方法的混合迭代，在图像边缘得到保护的同时，取得了较其它算法更好的抑斑能力与视觉效果，而在运算速度上，本文算法也要远远优于扩散滤波与变换域滤波算法。另外，本文提出的 SAR图像噪声方差估计新方法，比传统方法更加便捷有效。

[1]尹奎英,胡利平,刘宏伟,等.一种复合的 SAR 图像去噪算法[J].西安电子科技大学学报,2010,37(2): 224-230.Yin Kui-ying,Hu Li-ping,Liu Hong-wei,et al..Composite enhancing and denoising algorithm for SAR images based on scale space correlation[J].Journal of Xidian University,2010,37(2): 224-230.

[2]Lee J S.A simple speckle smoothing algorithm for synthetic aperture radar images[J].IEEE Transactions on System,Man,and Cybernatics,1983,13(1): 85-89.

[3]Lopes A,Touzi R,and Nezry E.Adaptive speckle filters and scene heterogeneity[J].IEEE Transactions on Geoscience and Remote Sensing,1990,28(6): 992-1000.

[4]凤宏晓,焦李成,侯彪.基于局部平移瑞利分布模型的 SAR图像相干斑抑制[J].电子与信息学报,2010,32(4): 925-931.Feng Hong-xiao,Jiao Li-cheng,and Hou Biao.SAR image despeckling based on local translation-rayleigh distribution model[J].Journal of Electronics＆Information Technology,2010,32(4): 925-931.

[5]Bhuiyanr M I H,Ahmad M O,and Swamy M N S.Spatially adaptive wavelet-based method using the cauchy prior for denoising the SAR images[J].IEEE Transactions on Circuits and Systems for Video Technology,2007,17(4): 500-507.

[6]贾建,陈莉.基于双变量模型和非下采样 Contourlet变换的SAR图像相干斑抑制[J].电子与信息学报,2011,33(5):1088-1094.Jia Jian and Chen Li.SAR image despeckling based on bivariate threshold function in NSCT domain[J].Journal of Electronics＆Information Technology,2011,33(5):1088-1094.

[7]常霞,焦李成,刘芳,等.基于斑点方差估计的非下采样Contourlet域SAR图像去噪[J].电子学报,2010,38(6): 1-6.Chang Xia,Jiao Li-cheng,Liu Fang,et al..Sar image despeckling based on the estimation of speckle variance in nonsubsampled contourlet domain[J].Acta Electronica Sinica,2010,38(6): 1-6.

[8]凤宏晓,侯彪,焦李成,等.基于非下采样Contourlet域局部高斯模型和 MAP的 SAR图像相干斑抑制[J].电子学报,2010,38(4): 811-816.Feng Hong-xiao,Hou Biao,Jiao Li-cheng,et al..SAR image despeckling based on local gaussian model and MAP in NSCT domain[J].Acta Electronica Sinica,2010,38(4):811-816.

[9]Yu Y and Acton S.Speckle reducing anisotropic diffusion[J].IEEE Transactions on Image Processing,2002,11(11):1260-1270.

[10]Yu Jin-hua,Wang Yuan-yuan,and Shen Yu-zhong.Noise reduction and edge detection via kernel anisotropic diffusion[J].Pattern Recognition Letters,2008,29(10):1496-1503.

[11]Liu Guo-jin,Zeng Xiao-ping,Tian Feng-chun,et al..Speckle reduction by adaptive window anisotropic diffusion[J].Signal Processing,2009,89(11): 2233-2243.

[12]Kass M,Witkin A,and Terzopolos D.Snakes: active contour models[J].International Journal of Computer Vision,1988,1(4): 321-331.

[13]Weickert J and Kühne G.Fast methods for implicit active contour models.Geometric Level Set Methods in Imaging,Vision,and Graphics[C].2003,Part II: 43-57.

[14]Lee J S and Eric P.Polarimetric Radar Imaging: From Basics to Applicaion[M].Boca Raton: CRC Press of Taylor ＆ Francis Group,2009: 101-175.