立方体人工鱼礁背涡流的三维涡结构

李晓磊，栾曙光，陈勇，张瑞瑾

(1.大连海洋大学海洋与土木工程学院，辽宁大连116023;2.大连海洋大学辽宁省海洋牧场工程技术研究中心，辽宁大连116023;3.大连海洋大学海洋科技与环境学院，辽宁大连116023)

人工鱼礁即人为设置在水域中的构造物，用以改善、修复和优化水生生物栖息环境，为鱼类等生物提供索饵、繁殖、生长、发育等场所，达到保护、增殖资源和提高渔获质量的目的［1］。人工鱼礁投放到海底后会产生多种效应，如饵料效应、流场效应等，其中流场效应对于鱼礁诱集鱼类十分关键［1］。投放人工鱼礁后的海域，由于礁体的阻流作用，流场重新分布形成新的流场，在鱼礁后方形成滞流区或缓流区［2-6］，通常在礁体后方形成一个充满漩涡的背涡流区域。人工鱼礁背涡流区域水流流速减缓、水流方向改变，很多饵料生物聚集，为鱼类提供了良好的索饵场所。日本学者在鱼礁区现场观测到很多鱼类聚集在人工鱼礁背涡流区域活动，从而证实了人工鱼礁具有诱集鱼类的作用和效果［7-9］。

目前，国内外对人工鱼礁的研究手段主要有物理模型试验、风洞试验、数值模拟等，研究结果多为二维空间上的定性及定量研究［10-13］。刘同渝等［4］针对梯形、三角锥体、堆叠式鱼礁模型进行了水槽和烟风洞试验，结果显示，鱼礁两侧为缓流区，范围约为鱼礁体的1/3;鱼礁背部为涡流区，影响范围可达礁体长度的2～3倍，礁体背流面涡流渐远渐弱。张硕等［14］研究了6种不同高度长方体鱼礁模型的流场效应，结果表明，混凝土模型礁产生的背涡流长度、高度、面积均随礁高的增加而增加。刘洪生等［15］针对正方体、金字塔及三棱柱人工鱼礁模型，通过风洞试验研究不同类型人工鱼礁单体和不同组合正方体模型的流场效应，结果表明，鱼礁模型背流面产生的背涡流规模随来流速度的增大而增大，相同来流速度下空心模型的背涡流规模较相同形状的实心模型小，空心模型背涡流回流速度随模型空隙率的增大而减小。潘灵芝等［16］对实心方块体的研究表明，鱼礁产生的背涡流域的规模随礁高的增大而增大。但目前尚未见到关于背涡流三维涡结构方面的研究报道。为此，本研究中作者应用CFD软件对立方体人工鱼礁在定常流作用下的三维流场进行了数值模拟试验，针对立方体人工鱼礁背涡流的三维涡结构展开讨论，分析了涡旋结构的形状、几何尺寸、涡心位置和涡旋的流速分布，旨在揭示背涡流的三维涡结构。

1 数学模型

1.1 基本假设

经过对计算对象鱼礁周围流体特性的分析，做出如下基本假设［16-17］:

1)海水为不可压缩、定常、黏性流体;

2)不考虑流场中的温度变化;

3)流体为具有自由水面的牛顿流体。

1.2 流体动力学控制方程

数值计算遵循质量守恒和动量守恒定律，控制方程是这些守恒定律的数学描述，不可压缩流体的控制方程为连续方程1和动量守恒方程2(即Navier-Stokes方程，简称 N-S 方程)［18］:

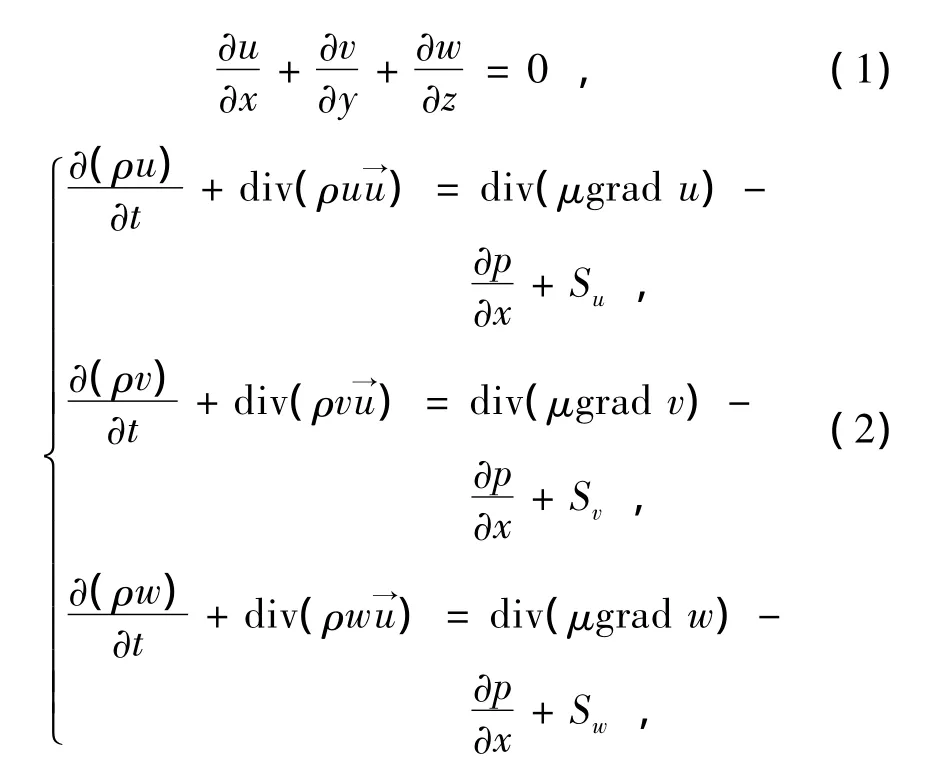
其中:u、v和w分别为x、y和z方向速度的分量;t为时间;为速度矢量;μ为动力黏度;p为压力;div为散度;grad为梯度;Su、Sv和Sw为动量守恒方程的广义源项。

1.3 湍流控制方程

在关于湍动能k方程的基础上，再引入一个关于湍动耗散率的方程，便形成了k-ε两个方程模型，称为标准k-ε模型 (standard k-ε model)。

标准k-ε模型的湍动能k和耗散率ε方程如下:

1.4 模型及参数的确定

三维流场数值模拟试验模拟近岸海域水深为15 m，施加定常流速为0.8 m/s，鱼礁模型为2 m×2 m×2 m(长×宽×高)的立方体，礁体迎流面与来流方向垂直。数值模拟的空间坐标中心选在礁体底面形心处，礁体位于模拟流场的中间位置，礁体和流场均与礁体水流方向垂直中心面 (以下简称垂直中心面，即XOZ面)对称［15］。

2 背涡流的三维涡结构

涡旋主要是由于水流在运动过程中受到外界礁体干扰后水流失去稳定而产生的。它是利用水流与鱼礁边界的离解现象，在靠近鱼礁固体边界附近形成回流区，增强水流各部分之间的相对运动，在主流与回流的交界面上形成较大的速度梯度，从而产生涡旋。背涡流三维涡结构由展向涡和流向涡组合而成。

2.1 展向涡

图1为数值模拟试验得到的水平截面沿水流方向 (XOY面)的流速矢量图。从图1可见，由于受到礁体的阻挡，水流在礁体侧面形成一对附着在其上且呈三角形状的涡旋区;当水流流经礁体背面和侧面相交的固体边界时涡旋脱落，并在礁体下游产生与礁体相接的椭圆涡对，称其为展向涡［19］。

经过对礁体不同高度水平截面上的展向涡进行比较发现，各个水平截面上展向涡两个涡旋的形状与礁体垂直中心面对称，并呈现出以水流方向为长轴的椭圆型;以涡心为中心其流速向外呈现逐渐增加的趋势，涡旋边界的最大流速约为来流流速的三分之一。其中一个涡旋的旋转方向为顺时针，而另一个涡旋的旋转方向为逆时针。数值模拟试验结果与Teneda［20］采用流体显示技术，在低雷诺数时圆柱绕流产生的圆柱尾涡 (双涡)的结果相吻合，Teneda的试验结论目前仍是数值模拟工作者验证算法准确性的标准之一。图2为不同水平截面(XOY)沿水流方向的流速矢量图，由于水流受到底摩阻的作用，在流场底面上流速近似为零，在高度约为0.1 H的水平截面上，展向涡两个涡旋涡心间的距离约为礁宽B的1.27倍;涡心距离礁体背流面的距离约为礁宽B的0.91倍;涡心处展向涡宽度约为礁宽B的1.83倍;展向涡长度约为礁长L的2.63倍，均出现最大值 (图3)。随着水平截面高度 (Z向)的增加，涡心间距、涡心距礁体背流面的距离逐渐减小，但变化比较平缓;涡心处展向涡宽度和长度也呈逐渐减小趋势。即随着水平截面高度的增加，两个涡旋逐渐向礁体背流面靠近，且涡旋的几何尺寸逐渐减小，呈金字塔形变化趋势，但始终呈椭圆形的对称涡对。当水平截面高度达到0.7 H时，展向涡的涡旋消失，即展向涡高度约为礁高H的0.7倍。展向涡流速的分布为从下到上由外向内逐渐减小，涡心处流速趋近于零。上述三维涡结构的几何尺寸与试件具有相同的比例，并与Tecplot软件给出的结果一致。

图1 展向涡水平截面 (XOY)沿水流方向的流速矢量图Fig.1 Flow velocity vector diagram along flow direction of streamwise vortex in horizontal section(XOY)

图2 不同水平截面 (XOY)沿水流方向的流速矢量图Fig.2 Flow velocity vector diagram along flow direction in diffent horizontal sections(XOY)

2.2 流向涡

图4为数值模拟试验得到的礁体垂直中心面(XOZ)的流速矢量图。由图4可见，由于受到礁体的阻挡，流经礁体上表面的水体在其上形成三角形状的涡旋区，当水流流经礁体上表面与背流面相交的固体边界时涡旋脱落，并形成一个外轮廓酷似直角三角形、以平行于直角三角形斜边且过涡心的直线为长轴的椭圆涡旋，称其为流向涡［19］。

对礁体不同垂直平面 (XOZ)流向涡进行比较，可以发现在礁体两侧距垂直中心面相同距离的垂直平面上，流向涡的形状关于礁体垂直中心面对称。流向涡在礁体垂直平面上呈现出外轮廓酷似直角三角形、以平行于斜边且过涡心的直线为长轴的椭圆形涡旋。

图5为不同垂直截面 (XOZ)的流速矢量图，在礁体垂直中心面，即Y=0截面上，涡心高度约为礁高H的0.69倍;涡心距礁体背流面的距离约为礁宽B的0.51倍;涡心处流向涡高度约为礁高H的1.14倍;流向涡长度约为礁长L的2.42倍，均出现最大值。在离开垂直中心面的各个垂直截面上，涡心高度、涡心处流向涡高度及流向涡长度均呈现逐渐减小的趋势;而涡心距礁体背流面的距离有逐渐增大的趋势 (图6)。流向涡在垂直中心面上产生的涡旋几何尺寸最大;随着远离礁体垂直中心面，流向涡的几何尺寸逐渐减小，在Y＞0.6B的垂直截面上流向涡消失。流向涡宽度约为礁宽B的1.2倍。流向涡的流速分布为由外向内逐渐减小，涡心处流速趋近于零。上述三维涡结构的几何尺寸与试件具有相同的比例，并与Tecplot软件给出的结果一致。

3 分析

将展向涡和流向涡与背涡流流场进行比较后发现:展向涡宽度大于流向涡宽度，展向涡宽度与背涡流流场宽度近似相等，即展向涡的宽度决定背涡流流场宽度;流向涡高度大于展向涡高度，流向涡涡心位置处的涡流高度与背涡流的高度近似相等，即流向涡的高度决定背涡流流场高度;展向涡和流向涡长度近似相等，并且与背涡流的长度近似相等，即展向涡和流向涡长度决定背涡流流长的长度。展向涡中各点的流速是背涡流流速矢量在水平方向的投影，流向涡中各点的流速是背涡流相应点流速矢量在垂直截面的投影，其绝对值均小于背涡流相应点水流速度的绝对值。

本研究数值模拟试验得出的立方体人工鱼礁流向涡高度约为礁高H的1.14倍这一结论，与刘洪生等［15］得出的背涡流高度为礁高的1.06～1.75倍的结论相吻合。展向涡长度为礁长L的2.63倍，流向涡长度约为礁长L的2.42倍，与刘洪生等［15］得出的背涡流长度为礁长的2.02～3.73倍相吻合，同时也与刘同渝等［4］得出的背涡流长度为礁长的2～3倍相吻合。展向涡宽度约为礁宽B的1.83倍，因此，背涡流宽度也约为礁宽B的1.83倍。

4 结论

黑木敏郎等［7］、张硕等［14］、刘洪生等［15］、潘灵芝等［16］、付东伟等［21］通过物理模型试验、风洞试验和数值模拟等方法，得到的关于背涡流的研究成果仅局限于流域规模，对其长度、高度及礁体背涡流的面积进行定量描述。本研究中以立方体人工鱼礁为例，在三维流场数值模拟试验的基础上，揭示了背涡流流场的三维涡结构，对不同礁高水平面上展向涡和不同垂直面上流向涡的形状、位置、几何尺寸及流速分布展开研究，为读者呈现了清晰的背涡流三维涡结构，得到如下结论:

1)展向涡和流向涡构成了立方体人工鱼礁背涡流的三维涡结构。

2)展向涡在水平截面上呈现一对以水流方向为长轴的椭圆型涡旋;在流场底面上流速近似为零;在0.1倍礁高的水平截面上涡漩几何尺寸达到最大值，随着水平截面高度 (Z向)的增加，涡漩的几何尺寸逐渐减小，涡旋逐渐向礁体背流面靠近，但始终呈现椭圆形的涡对;在0.7倍礁高的水平面上展向涡消失。展向涡流速的分布从下到上，由外向内逐渐减小，涡心处流速趋近于零。

3)流向涡在礁体垂直平面上呈现出外轮廓酷似直角三角形、以平行于斜边且过涡心的直线为长轴的椭圆形涡旋。在礁体垂直中心面上流向涡的几何尺寸达到最大值，远离礁体垂直中心面时流向涡的几何尺寸逐渐减小，在距离礁体垂直中心面约0.6倍礁宽处，流向涡涡旋消失。流向涡的流速由外向内逐渐减小，涡心处流速趋近于零。

4)展向涡的宽度决定背涡流流场宽度，流向涡高度决定背涡流流场高度，展向涡和流向涡长度近似相等，并决定背涡流流场的长度。展向涡和流向涡在各点的流速矢量均小于背涡流相应点水流速度的绝对值。

图3 展向涡在不同水平截面 (XOY)上的几何尺寸变化Fig.3 Geometry size of streamwise vortex in different horizontal sections(XOY)

图4 流向涡垂直中心面 (XOZ)的流速矢量图Fig.4 Flow velocity vector diagram along flow direction of crosswise vortex in vertical central plane(XOZ)

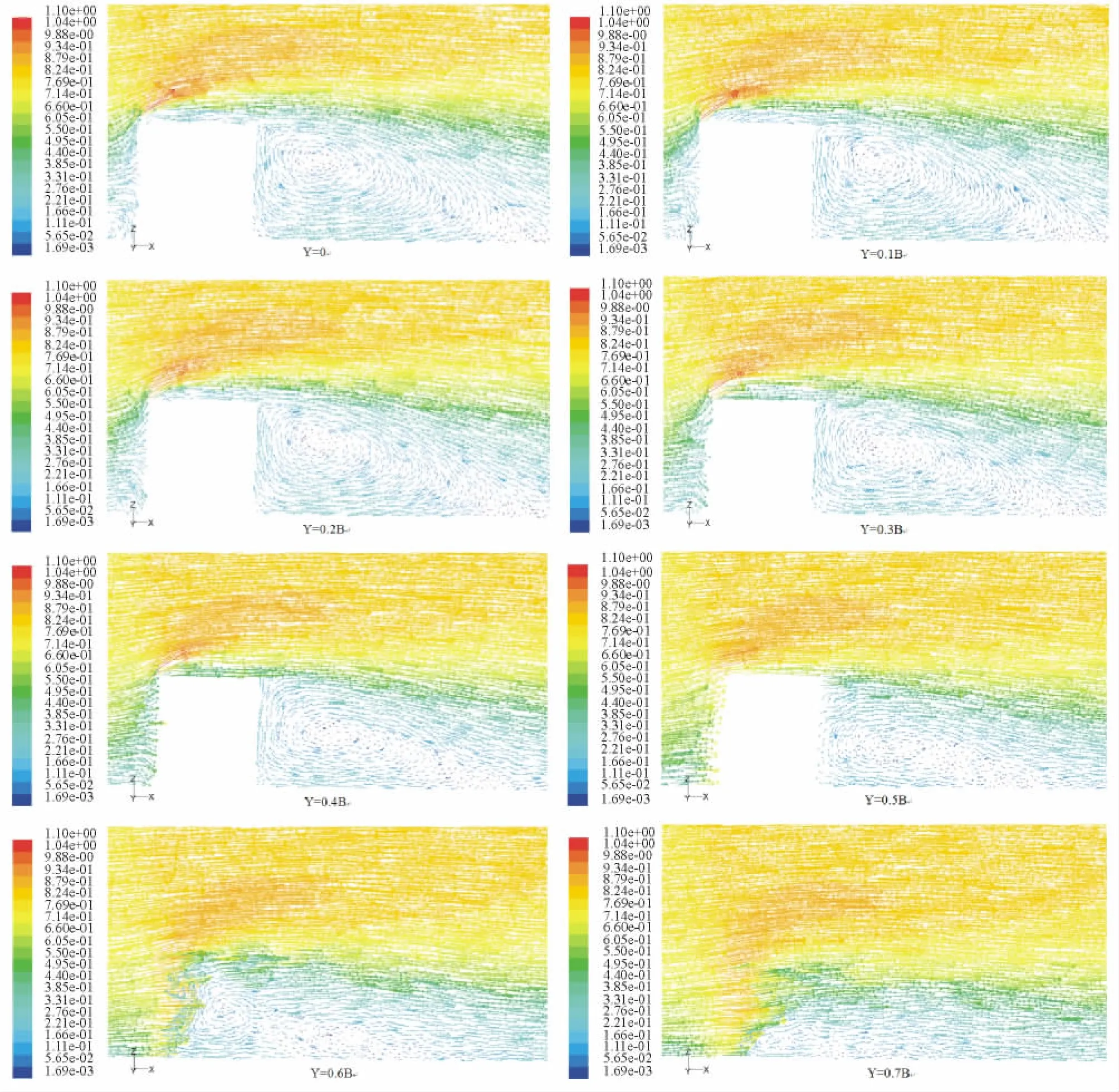
图5 不同垂直截面 (XOZ)的流速矢量图Fig.5 Flow velocity vector diagram along flow direction in diffent vertical planes(XOZ)

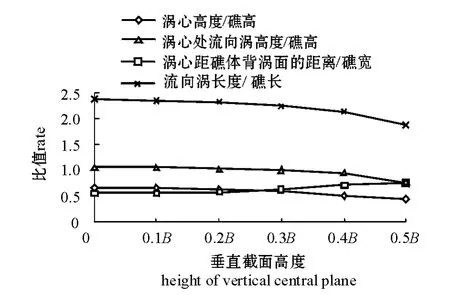
图6 流向涡在不同垂直截面 (XOZ)上的几何尺寸变化Fig.6 Geometry size of crosswise vortex in different vertical central planes(XOZ)

［1］王波，武建平，高峻，等.关于青岛建设人工鱼礁改善近海生态和渔业环境的探讨［J］.海岸工程，2004，23(4):66-73.

［2］陈勇，于长清，张国胜，等.人工鱼礁的环境功能与集鱼效果［J］.大连水产学院学报，2002，17(1):65-69.

［3］刘同渝，陈勤儿，黄汝堪，等.鱼礁模型波浪水槽试验［J］.海洋渔业，1987(1):9-12.

［4］刘同渝.人工鱼礁的流态效应［J］.水产科技，2003(6):43-44.

［5］斯广杰，陈丕茂，杜飞雁，等.深圳杨梅坑人工鱼礁区投礁前后大型底栖动物种类组成的变化［J］.大连海洋大学学报，2010，25(3):243-247.

［6］卢璐，张硕，赵裕青，等.海州湾人工鱼礁海域沉积物中重金属生态风险的分析［J］.大连海洋大学学报，2011，26(2):126-132.

［7］黑木敏郎，佐藤修，尾崎晃.焦礁樽造物理学的研究Ⅰ［M］.函馆:北海道水产部，1964:1-19.

［8］影山芳郎，大阪英雄，山田英巳，等.水槽実験 による 多孔立方体魚礁 モデル周り可視化［J］.水産土木，1980，17(1):1-10.

［9］中村充.流環境から人工礁漁場［J］.水産土木，1979，15(2):5-12.

［10］张怀慧，孙龙.利用人工鱼礁工程增殖海洋水产资源的研究［J］.资源科学，2001，23(5):6-10.

［11］吴静.人工鱼礁集鱼效果的初步研究［D］.上海:上海水产大学，2005.

［12］Santos M，Monteiroc C.The artificial reef system(south Portugal):Fish assemblages and fishing yield［J］.Fisheries Research，1997，30(1-2):33-41.

［13］William S J R.Artificial reef evaluation［M］.USA:CRC Press，2002:83-86.

［14］张硕，孙满昌，陈勇.不同高度混凝土模型礁背涡流特性的定量研究［J］.大连水产学院学报，2008，23(4):278-282.

［15］刘洪生，马翔，章守宇，等.人工鱼礁流场效应的模型实验［J］.水产学报，2009，33(2):229-236.

［16］潘灵芝，林军，章守宇.铅直二维定长流中人工鱼礁流场效应的数值实验［J］.上海水产大学学报，2005，14(4):406-412.

［17］金泰木，张明，李连奎.CFD在客车空调系统设计中的应用［J］.铁道车辆，2003，41(3):20-22.

［18］王福军.计算流体动力学分析——CFD软件原理与应用［M］.北京:清华大学出版社，2004.

［19］Williamson C H K.The natural and forced formation of spot-like dislocations in the transition of a wake［J］.Fluid Mech，1992，243:393-441.

［20］Taneda S.Experimental investigation of the wakes behind cylinder and Plates at low Reynolds numbers［J］.Phys Soc Jpn，1956，11:302-306.

［21］付东伟，栾曙光，张瑞瑾，等.人工鱼礁开口比和迎流面形状对流场效应影响的双因素方差分析［J］.大连海洋大学学报，2012，27(3):274-278.