基于SHPB装置的膨胀圆柱管实验技术＊

叶想平，李英雷，李英华

（中国工程物理研究院流体物理研究所冲击波物理与爆轰物理重点实验室，四川 绵阳 621900）

金属壳体在冲击载荷作用下的断裂时间和断裂过程预测是工程实践和武器研究中非常关注的问题。很多工程问题，如导弹、炮弹、壳体战斗部外壳的膨胀断裂，输油、输气管道和压力容器的爆裂。核电站防护层和管道材料的辐射脆化、热冲击安全、建筑物和结构中壳体部件抗冲击能力评估等，都涉及结构的动态断裂性能评估和灾后对策问题，因此研究金属壳体的动态断裂行为，一直受到重视。早在20世纪40年代，N.F.Mott、G.I.Taylor、R.Gurney等就对壳体内部向外爆轰加载条件下的断裂问题做过深入的研究，分别提出了Mott碎片分布公式［1］、Taylor断裂模型［2］和Gurney碎片初始速度经验公式［3］，随后D.Grady［4］总结并进一步推进了这方面的研究。

目前普遍采用膨胀管或膨胀环实验技术对薄壁圆柱管（环）进行实验研究［5－7］。膨胀管和膨胀环实验技术的测试手段分别为高速摄影技术［5］和 VISAR（或DISAR）［6－7］，通过分析圆管（环）径向膨胀速度（或位移）时程曲线，获取圆柱管（环）径向膨胀运动状态，包括径向膨胀应变和应变率等，加载应变率在104～106s－1。此外膨胀环还可用于材料在高应变率拉伸加载下的本构关系研究。膨胀管（环）实验回收碎片的断口扫描和金相分析一般用于获得断口形貌及碎片内部的金相特征，辅助开展圆柱管膨胀断裂机理研究，但由于难以实施冻结回收，因此不能有效观察裂纹萌生和扩展过程。R.E.Winter［8］将Taylor杆加以改进，在圆柱管内填充尼龙，通过尼龙被子弹撞击挤压后的膨胀作用，实现对圆柱管的膨胀加载，但仍旧无法对试样进行冻结回收。为了更直观地研究圆柱管在高应变率加载下膨胀断裂的断裂机理，必须发展一套有效的冻结回收实验技术，以便展示圆柱管的膨胀断裂过程，更深入地研究其断裂机理。

本文中，采用改进的霍普金森压杆实验装置，通过调节载荷脉宽来控制圆柱管径向膨胀变形量，获得不同膨胀状态的回收圆柱管。除实时监测圆柱管膨胀过程中凸起最严重位置处的径向应变、应变率外，还发展凸起最严重位置处环向应力及内压载荷的测量能力，并提供断裂时刻的准确判断方法。

1 实验原理

实验装置为改进的霍普金森压杆［9］，如图1所示，实验中透射强度很低，故去掉吸收杆。实验装置通过轴向压缩填充材料，实现对圆柱管的径向膨胀加载。调节入射杆端部凸起部分与制动块之间的间距可控制样品加载位移量，实现冻结回收。在圆柱管入射端外壁面环向粘贴应变片可检测圆柱管断裂时间。实验中，圆柱管膨胀变形前后对比如图2所示。与滑移爆轰实验［10］类似，圆柱管受载后将沿轴向非均匀膨胀变形，并且凸起膨胀位置随载荷增加沿轴向移动。圆柱管凸起最严重位置是圆柱管最容易发生破坏的位置，也是研究关注的位置，因此，实验中也最为关心圆柱管凸起变形最严重位置处的应力、应变、应变率。

图1 改进的SHPB实验装置示意图Fig.1 Schematic of improved SHPB setup

除SHPB实验基本假设外［11］，实验还采用如下基本假设：（1）填充物低剪切强度，视为流体处理，于是忽略填充物自身塑性变形对载荷的损耗，以便测量圆柱管内压载荷和环向拉伸应力；（2）填充物体积不变，即填充物体积不可压且实验过程中无泄漏，避免载荷损耗在填充物体积变形和泄漏上，载荷能量将全部用于对圆柱管进行膨胀加载，便于提高载荷利用率，并且方便应变处理换算。

由数值模拟可得不同载荷强度下圆柱管凸起破裂处实测径向应变εr与通过体积不变假设换算得到的填充物均匀径向应变εq之间的函数关系形式。结合不同载荷强度下实验所得εr与εq之间函数关系的具体参数，最终确定函数关系式εr＝f（εq）。当圆柱管发生破裂时，通过圆柱管上应变片信号陡变判断断裂时刻，结合的测量结果，即可确定圆柱管凸起破裂处径向断裂应变、应变率。

式中：σθ为圆柱管凸起最严重位置处的环向拉伸应力，r1和r2分别为圆柱管初始内径和外径，E为杆的弹性模量，A0和A1分别为杆和垫块的横截面积。当圆柱管发生断裂时，可通过判断的断裂时刻和p、σθ测量结果，确定圆柱管断裂时刻凸起最严重位置处的环向拉伸应力和内压载荷。

2 数值模拟分析

采用LS－DYNA二维轴对称模型模拟薄壁45钢圆柱管膨胀实验，选用162号平面轴对称单元。分离式霍普金森压杆几何尺寸为∅14.5mm×1m，弹长为287.5mm。为提高圆柱管的加载应变率，圆柱管壁厚和内径按最小加工能力设计：壁厚，0.5mm；内径，7mm；长度，10mm。填充物（石蜡）长度为6mm，垫块尺寸为∅7mm×16mm。在实验设计初期，通过数值模拟来确定合适的圆柱管和填充物模型尺寸，以节省实验消耗，同时还要确定εr＝f（εq）函数关系式。载荷波形选择与拟用的实验波形相同，直接从霍普金森压杆入射端面输入。

霍普金森压杆、垫块和填充物的材料参数如表1所示，表中ρ为密度，E为弹性模量，K为体积模量，μ为泊松比。

表1 材料参数Table1 Parameters for materials

圆柱管材料的J－C本构关系［12］为

式中：σ为应力，ε为塑性应变，A为材料静态屈服应力，B为应变硬化系数，n为应变硬化指数，C为应变率敏感系数，m 为温度敏感系数，Tr为参考温度（一般取室温），Tm为材料熔点温度；＊＝／0，0为参考应变率（可取准静态加载下的应变率）。

该圆柱管材料的 Grüneisen状态方程和J－C本构参数［12］分别为：ρ，7.896kg／m3；E，212GPa；μ，0.3；cp，452J／（kg·K）；A，350MPa；B，275MPa；C，0.022；n，0.36；m，1.00；Tr，298K；Tm，1 811K。

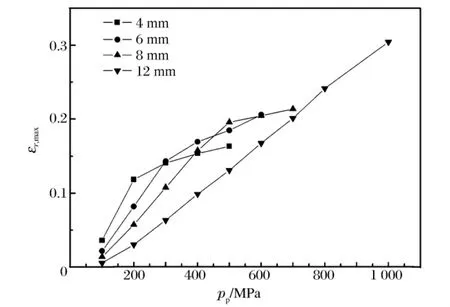
图3 在不同的填充物长度下，圆柱管径向最大应变随峰值载荷的变化Fig.3 Variation of the maximum radial strain of cylinder with peak load in the different cases in which the length of the filler is different

图3中4、6、8和12mm为石蜡填充长度。填充物长4mm时，由于实验过程中填充物会向两侧间隙填充，圆柱管所能达到的最大径向应变在0.18左右（圆柱管断裂应变为0.21），不能实现对圆柱管的断裂加载；当填充物长12mm时，又会极大地降低载荷利用率。实现圆柱管断裂应变的载荷强度需增加到700MPa，而本次实验所用压杆允许的最高安全载荷强度为600MPa。因此填充物长度应在满足圆柱管径向断裂应变量的前提下，越短越好。同时模拟显示，垫块伸入圆柱管长度为2～3mm即可满足封装填充物的要求，因此本次实验中填充物长度选为6mm，圆柱管长度为10mm。

数值模拟所得εr与εq之间关系如图4所示。在无加载条件下应当有εq＝εr＝0。由于填充物会向样品与垫块间间隙空腔内填充，εr和εq不能无限增大，其取值当存在某一上限，结合图4中曲线走势，最终采用过原点的抛物线拟合关系式为

图4 数值模拟中不同载荷下圆柱管径向应变拟合关系Fig.4 εr－εqrelationship of cylinder under different loadings by numerical simulation

图4中数据点为不同载荷强度下的εr与εq，实线为εr＝fε（）q拟合曲线。由于圆柱管同一处膨胀变形的径向应变和环向应变相同，因此以后不再强调环向应变量，仅描述径向应变和应变率。将垫块和填充物总长度视为样品长度，实验过程中填充物内压峰值均不会超过150MPa，导致垫块弹性变形最大值为6.7×10－4，因此数据处理中可忽略垫块弹性变形对数据处理的影响；组合样品的特征时间为9μs，而实验加载时间为160μs，因此垫块与杆端面波阻抗不匹配对实验造成的影响可以忽略［13］。圆柱管径向凸起破裂处径向（环向）应变、应变率分别为

式中：εr和εθ分别为圆柱管凸起破裂处的径向和环向应变和分别为圆柱管凸起破裂处的径向和环向应变率，a、b为实验待定系数，εi和εt分别为入射和透射应变波，c0为杆中一维应力弹性纵波波速，r和r0分别为填充物半径和初始半径，l和l0分别为填充物长度和初始长度。

3 实 验

实验结构与数值模拟的完全相同。其中，入射杆和圆柱管上应变片灵敏系数为1.73，透射应变波相对入射应变波弱，但透射杆上应变片灵敏系数为117，因此透射波电压信号与入射波电压信号幅度相当。实验结果如表2所示。

表2 实验参数Table2 Parameters in experiments

图5 实验中不同载荷下圆柱管径向应变拟合关系Fig.5 εr－εqrelationship of cylinder under different loadings by experiments

表2中l为填充物长度，D和D0分别为圆柱管凸起处直径和初始直径，v为子弹速度，η为填充物泄漏率，pp为填充物内压峰值。由表2实验数据拟合得式（4）～（5）中a＝0.515 5，b＝0.675 4，拟合效果见图5。实验1～8中，圆柱管均未发生断裂；实验9中，圆柱管中部裂开一小口，但未全部裂开；实验10中圆柱管完全断裂。图6为实验冻结回收柱管形貌图，回收柱管状态基本覆盖了膨胀变形、裂纹萌生及扩展过程。

实验采用的石蜡填充物强度为7MPa左右，相较于圆柱管材350MPa的屈服强度可忽略不计，满足填充物低剪切强度假设；圆柱管最大内压幅值为136MPa，石蜡最大被压缩量为3%，可忽略不计，石蜡体积压缩变形满足填充物不可压假设；通过记录实验前后石蜡重量，得到石蜡最大泄漏率为0.33%（见表2），满足填充物无泄漏假设。

图6 不同变形状态的实验样品Fig.6 Experimental samples subjected to different deformation

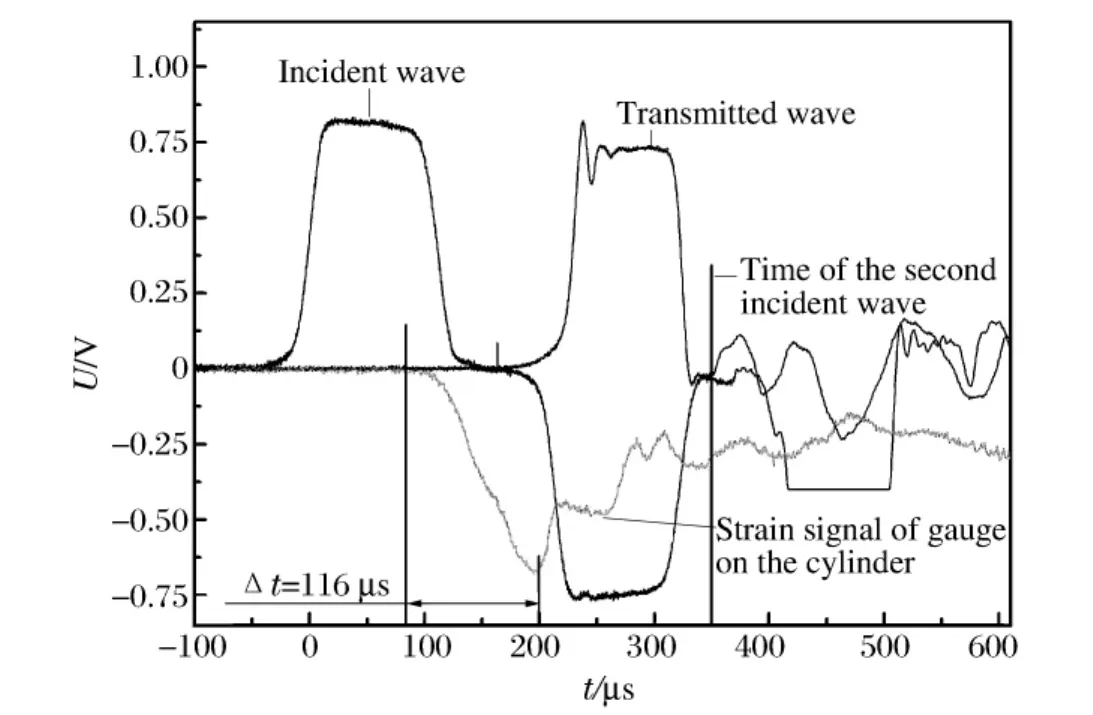
图7 （a）原始电压波形Fig.7 （a）Original voltage waveform

圆柱管完全断裂实验中，记录的原始波形，圆柱管凸起处径向（环向）应变、应变率、内压载荷和环向拉伸应力时程曲线如图7所示。

图7 （b）内压、环向拉应力和径向应变随时间的变化Fig.7 （b）Variation of pressure，circumferential tensile stress and radial strain with time

其中，σ为104s－1下的45钢压缩应力应变曲线。图7（a）中入射波反射回来后，在本应出现二次入射波的时刻（350μs），载荷被制动块有效吸收，未对样品进行二次加载，单次加载效果良好。圆柱管上应变片信号急剧下降时刻即为圆柱管发生断裂时刻，对应加载断裂时间为116μs，对应图7（b）便可得，圆柱管径向断裂应变为0.21、断裂时平均应变率为1.8×103s－1，环向拉伸断裂应力为914MPa。加载116μs时圆柱管断裂，圆柱管内压也开始降低，但下降幅度并不明显。主要原因为，在圆柱管发生断裂初期，由于圆柱管的惯性约束，圆柱管内压幅值并不会急剧降低（如图7（b）所示），因此仅由圆柱管内压幅值变化难以准确判定断裂时刻。圆柱管凸起变形最严重位置处为三维应力状态，因此，实验所得环向拉应力、应变、应变率曲线不能直接用来研究材料在高应变率拉伸载荷下的本构关系，如图7（c）所示。

SHPB实验装置加载时间为10－5～10－4s，而金属圆柱管膨胀断裂应 变 为 10－2～10－1，因 此 基 于SHPB装置的膨胀圆柱管实验技术加载应变率范围为102～104s－1。

图7 （c）压缩应力、环向应力和环向应变率随应变的变化Fig.7 （c）Variation of compressive stress，circumferential tensile stress and circumferential strain rate with strain

4 结 论

实现了对45钢薄壁圆柱管的膨胀断裂加载、冻结回收及相关实验量测量，具体结论如下：

（1）改进型霍普金森压杆可作为102～104s－1应变率范围内，金属圆柱管动态膨胀断裂的实验研究手段，能有效监测圆柱管凸起变形处从膨胀变形直至断裂过程中的径向应变、应变率、内压载荷和环向拉伸应力，能准确判断圆柱管的断裂时刻，以及径向断裂应变、应变率和环向拉伸断裂应力。

（2）通过控制实验载荷，可有效进行冻结回收实验，以观察圆柱管膨胀至裂纹萌生、扩展的全过程。

［1］Mott N F.A theory of fragmentation of shells and bombs［R］.1943.

［2］Taylor G I.The fragmentation of tubular bombs［C］∥Batchelor G K.The Scientific Papers of Sir Geoffrey Ingram Taylor：Vol.3.Cambridge：Cambridge University Press，1963：387－390.

［3］Gurney R W.The initial velocities of fragments from bombs，shell，grenades［R］.BRL Report No.405，1943.

［4］Grady D.Fragmentation of rings and shells［M］.Berlin：Springer Science＋Business Media Deutschland GmbH，2006.

［5］汤铁钢，谷岩，李庆忠，等.爆轰加载下金属柱壳膨胀破裂过程研究［J］.爆炸与冲击，2003，23（6）：529－533.TANG Tie－gang，GU Yan，LI Qing－zhong，et al.Expanding fracture of steel cylinder shell by detonation driving［J］.Explosion and Shock Waves，2003，23（6）：529－533.

［6］Warnes R H，Duffey T A，Karpp R R，et al.An improved technique for determining dynamic material properties using the expanding ring［M］∥Meyers M A，Murr L E.Shock Waves and High－strain－rate Phonomena in Metals.New York：Plenum Press，1981：23－36.

［7］Hoggatt C R，Recht R F .Stress－strain data obtained at high rates using an expanding ring［J］.Experimental Mechanics，1969，6（10）：441－448.

［8］Winter R E.Measurement of fracture strain at high strain rates［C］∥Proceedings of the 2nd Conference on Mechanical Properties of Materials at High Rates of Strain.1980：81－89.

［9］Gama B A，Lopatnikov S L，Jr Gillespie J W.Hopkinson bar experimental technique：A critical review［J］.Applied Mechanics Reviews，2004，57（4）：223－251.

［10］汤铁钢，李庆忠，孙学林，等.45钢柱壳膨胀断裂的应变率效应［J］.爆炸与冲击，2006，26（2）：35－39.TANG Tie－gang，LI Qing－zhong，SUN Xue－lin，et.al.Strain－rate effects of expanding fracture of 45steel cylinder shells driven by detonation［J］.Explosion and Shock Waves，2006，26（2）：35－39.

［11］胡时胜.霍普金森压杆技术［J］.兵器材料科学与工程，1991（11）：40－47.HU Shi－sheng.The techniques of Hopkinson pressure bar［J］.Ordnance Material Science and Engineering，1991（11）：40－47.

［12］Johnson G R，Cook W H.A constitutive model and data for metals subjected to large strains，high strain rates and high temperatures［C］∥Proceedings of the Seventh International Symposium on Ballistics.The Hague，The Netherlands，1983：541－547.

［13］Ravichandran G，Subhash G.Critical appraisal of limiting strain rates for compression testing of ceramics in a split Hopkinson pressure bar［J］.Journal of the American Ceramic Society，1994，77（1）：263－267.