基于随机子空间的异步电动机转子断条早期故障检测

王洪涛

(宁德师范学院物理与电气工程系，福建宁德 352100)

转子断条是笼型异步电动机的常见故障之一，可占电动机故障种类［1－3］的10%。由于电动机应用广、数量多，与生产、生活联系紧密，人们迫切希望能对电动机实现早期故障检测［4］。早期故障检测不仅能够保证生产安全，防患于未然，而且可为故障定位、决策和维修赢得时间，提高生产效率，减少经济损失，因此具有十分重要的意义。

对异步电动机转子断条的研究表明:当电动机发生转子断条时，定子电流将出现频率为fb=(1±2s)f1(s为转差率，f1为电网频率)的边频分量［5－7］。但在转子早期断条故障时，由于定子电流故障特征量微弱、电网频率波动，给早期故障检测带来了困难。

针对早期转子断条故障检测的难题，采用随机子空间方法，先用采集到的定子电流数据构成Hankel矩阵，再对Hankel矩阵进行QR分解和特征值分解，得到矩阵特征值，进而得到定子电流中基频分量和特征分量的频率值。通过仿真和实验验证了该方法的有效性。

1 随机子空间理论

随机子空间(SSI)方法是一种线性系统辨识方法［8－10］。对于线性系统离散状态模型为

式中:xk为离散的时间状态向量;A为系统矩阵;C为输出矩阵;wk和vk分别为零均值过程噪声和测量噪声，且互不相关。

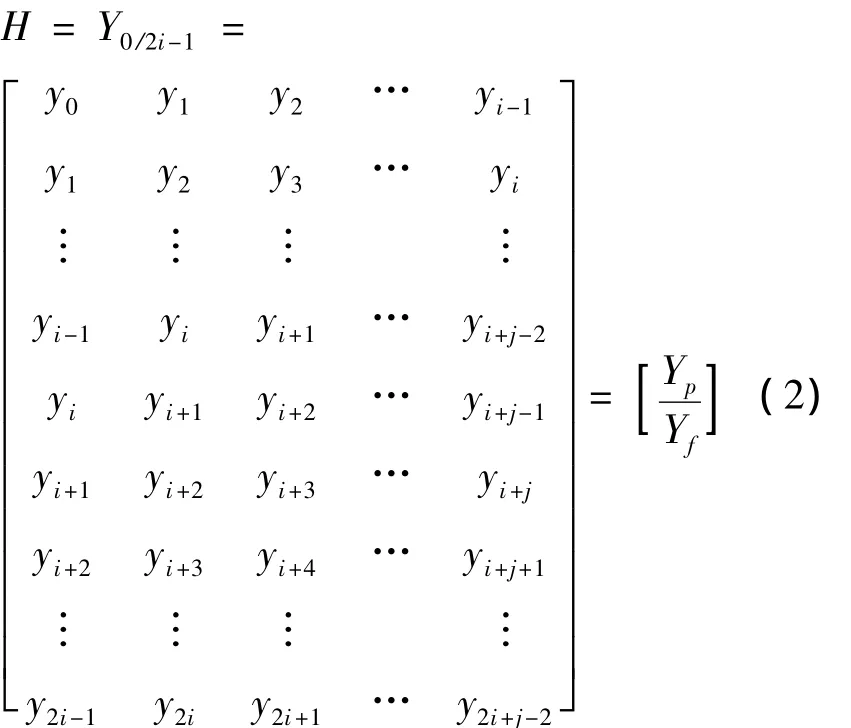
根据系统输出yk构造Hankel矩阵式中:Y0/2i－1的下标0/2i－1表示Hankel矩阵第1块行和最后1块行。对Hankel矩阵H进行QR分解，

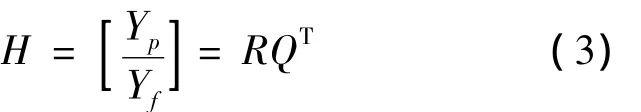
式中:Q和R表示QR分解得到的正交矩阵和下三角矩阵。定义“将来”输出的行空间在“过去”输出的行空间上的投影为

式中“*”表示求广义的逆运算。

系统矩阵A和输出矩阵C可由最小二乘法辨识得出:

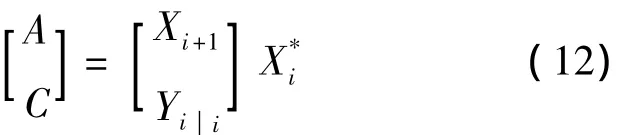
对系统矩阵A做特征值分解

其中:Λ =diag[ λ1，λ2… λi…λn]，λi为系统的特征值;Ψ = [ψ1，ψ2，…，ψn]为系统特征向量矩阵;n表示系统的阶次。

由系统的特征值，可得到输出信号的各个频率成分:

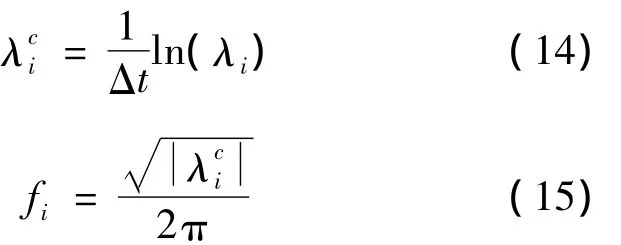
其中Δt表示采样时间间隔。

由输出信号频率fi，根据最小二乘辨识可进一步得出相应频率的幅值和相角［9］。

2 转子断条故障仿真和分析

转子断条故障的具体检测步骤:

1)待电机进入稳态运行后，采集转速信号和定子电流信号。

2)由转速信号求出电机转差率s。

3)由定子电流信号数据构造Hankel矩阵，按SSI方法识别电网频率f1和边频频率fb。

4)以fb、f1和s之间的关系fb=(1±2s)f1为判据，判断是否发生转子断条故障。

在Matlab7.1/Simulink环境下，采用文献［5］中模拟转子断条故障的方法，建立仿真模型，如图1所示。用异步电动机模块常用的绕线式异步电动机(50 Hp、400 V、50 Hz、1480RPM)代替笼型异步电动机，并在转子a相添加故障电阻Rrg=0.1Rr(Rr为异步电电动机转子电阻)模拟转子断条故障。

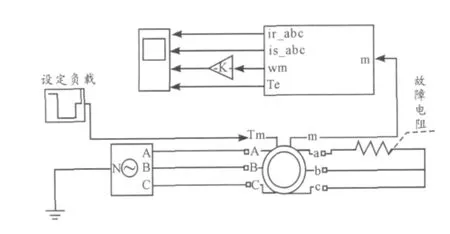
图1 转子断条故障仿真模型

设置电网频率f1的变化范围为50.5～49.5 Hz，UN=400 V，电机负载TN=238.75 N·m，转子 a相断条，采样频率fs=10 kHz。测量电机转速n，采集电机进入稳定运行时的定子电流ia，并在定子电流ia中加入0.01 A的直流分量和均值为零、信噪比SNR=80 dB的高斯白噪声，对ia人工染噪。图2为电网频率f1=50.5 Hz时，染噪后的定子电流ia波形和频谱。

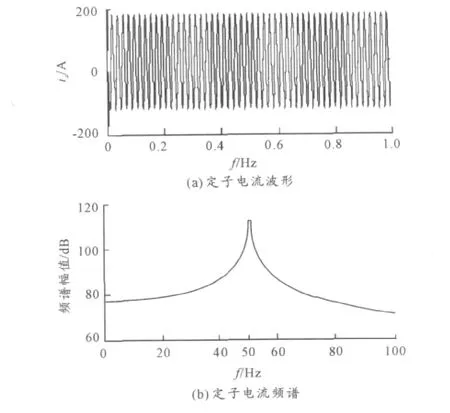
图2 定子电流波形和频谱

由图2可见，ia经FFT变换后的频谱中已难以检测出fb的频率值。

将ia电流信号数据构成Hankel矩阵，经SSI和最小二乘法辨识得到的ia电流幅值，如表1所示，可知基波分量的幅值约为边频分量的幅值的77倍，边频分量已被基波分量淹没。

表1 幅值测量结果

依次检测电网频率发生波动时，1根断条满载和80%负载以及2根断条满载的检测结果，见表2～4。根据转差率s和电网实时频率f1计算出边频频率fb的理论值，并与测量值对比，判断是否发生断条故障。

比较表2和表3可知，电动机满载时比80%负载时的测量精度高，并且电网频率波动越小，测量精度越高。当电网频率波动为+0.5 Hz时，边频频率fb最大测量误差为0.9875 Hz。比较表2和表4可知，故障程度越严重，检测精度越高。

综合以上比较结果，说明在强噪声(基频分量视为噪声)、轻微故障(断1根)、80%负载、电网频率偏移0.5 Hz的不利情况下，SSI方法仍能检测出转子断条故障。

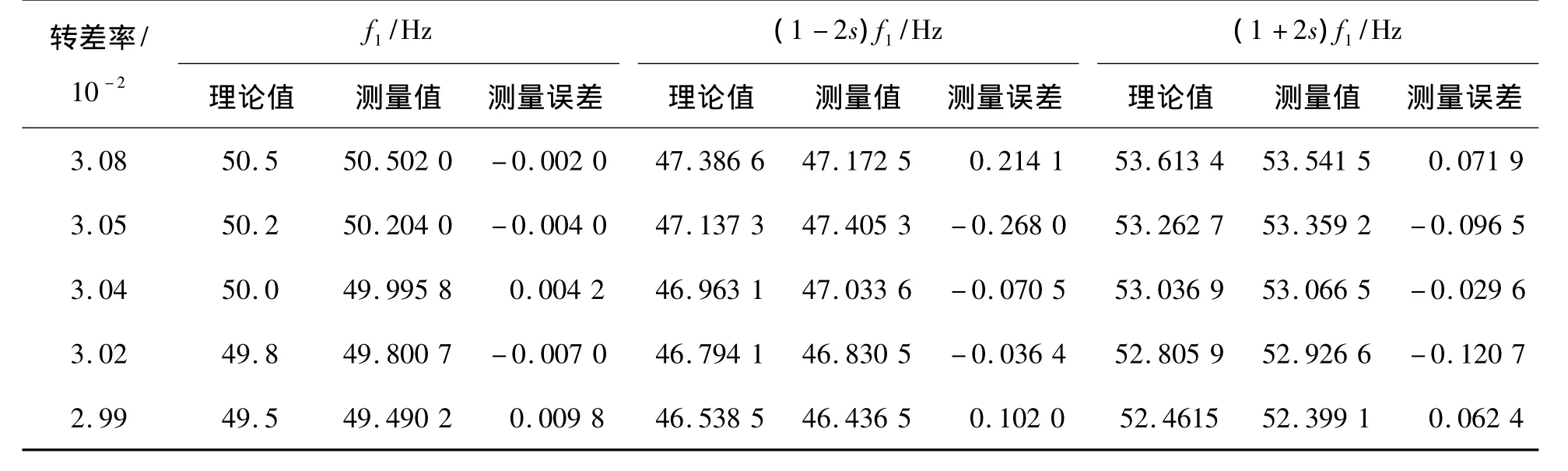
表2 转子断条1根、100%负载的检测结果

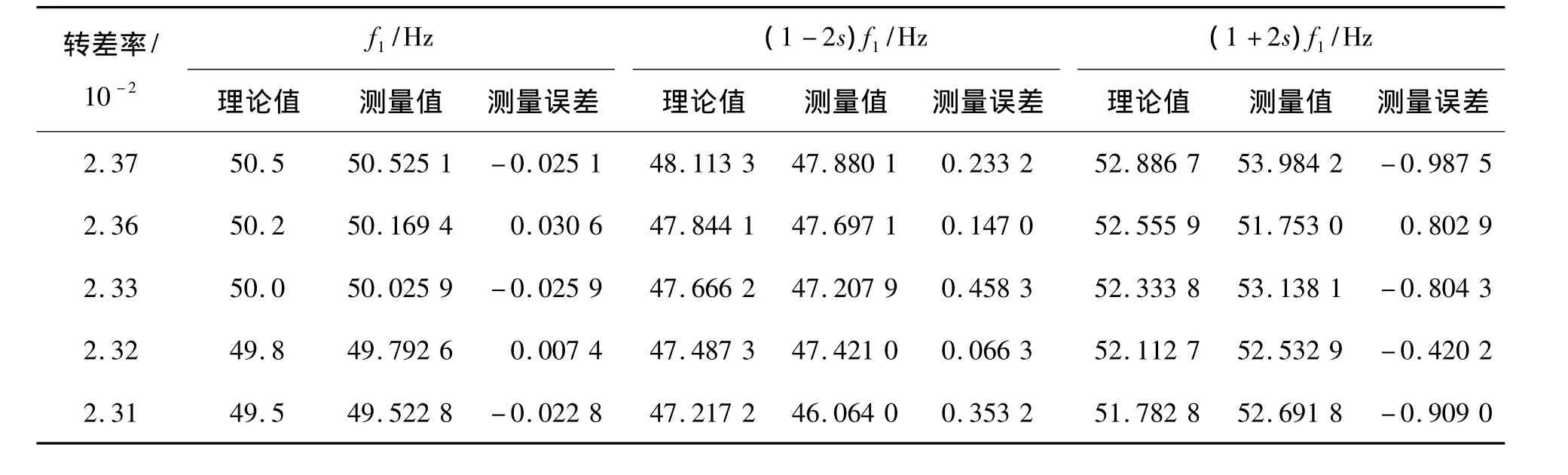
表3 转子断条1根、100%负载的检测结果

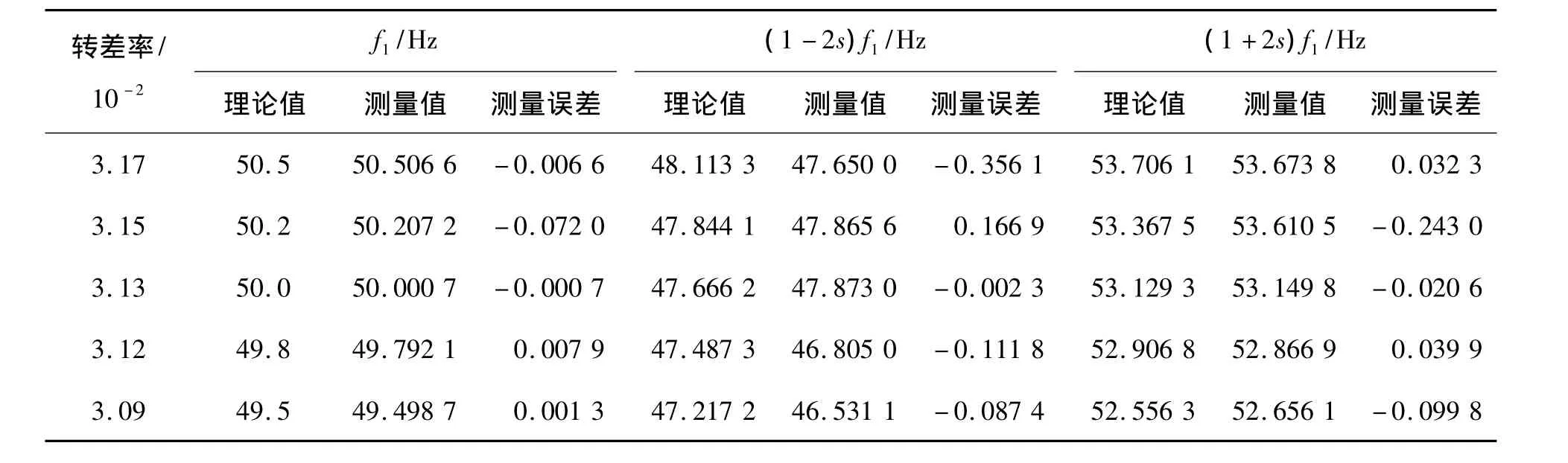
表4 转子断条2根、100%负载的检测结果

3 转子断条故障实验结果与分析

实验电机采用文献［11］中的Y100L－2型三相异步电机(3 kW、380 V、50 Hz、1 对极)和Y100L1－4型三相异步电机(2.2 kW、380 V、50 Hz、2对极)，按照图3完成实验接线。

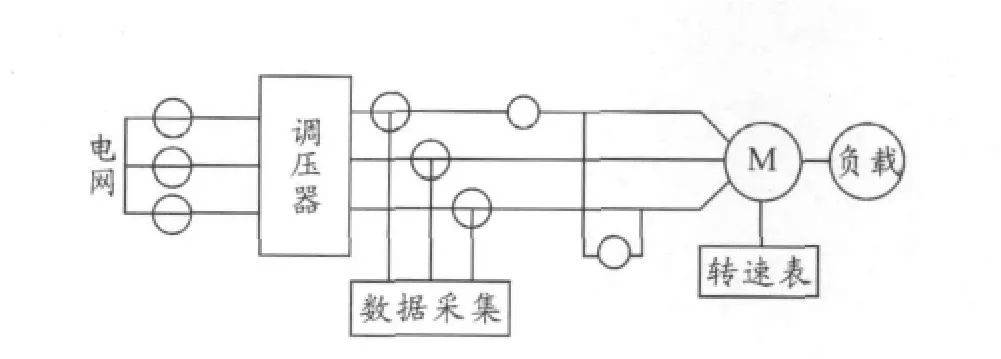
图3 实验接线

在Y100L－2型异步电动机带80%负载下，转子发生1根断条时的结果如表5所示。

表5 实验测量结果

由表5可知，电网频率发生了微小波动。SSI方法不仅测量出电网真实频率，而且以较高的精度测量出fb的频率值，且fb的测量值和理论值基本吻合，可以判定发生了转子断条故障。因为电网频率未知，故当精确测量出电网真实频率f1时，才能准确计算边频分量fb的理论值，进而判断fb理论值与测量值是否吻合，所以精确测量电网频率f1是有效检测的前提条件。

4 结论

1)检测步骤简便。直接采集定子电流数据进行检测，无需消噪处理。

2)抗干扰能力强。在强噪声背景、转子轻微断条、电机轻载时，准确检测出了定子电流的故障特征频率。

3)克服了电网频率波动和负荷波动带来的混淆，具有工程应用价值，为转子断条早期故障检测提供了新思路。

［1］张建文，马征宾，徐善琛，等.应用磁场摆角诊断异步电机转子断条故障［J］.高电压技术，2009，35(3):689－693.

［2］陈理渊，黄进.基于支持向量机的电机转子断条故障诊断［J］.电工技术学报，2006，21(8):48 －52.

［3］牛发亮，黄进.基于电磁转矩复解析小波变换的感应电机转子故障检测［J］.电工技术学报，2005，20(7):100－105.

［4］任震，张征平，黄雯莹，等.异步电动机早期故障检测技术发展评述［J］.华南理工大学学报:自然科学版，2001，29(11):67 －70.

［5］许伯强，宋佳伟，孙丽玲.变频供电异步电动机转子断条状态下变频器一次侧特征电流分析［J］.中国电机工程学报，2010，30(12):76 －79.

［6］张建文，王春生，张强.异步电机断条故障的启动电流小波诊断法［J］.高电压技术，2006，32(10):25 －28.

［7］牛发亮，黄进，杨家强，等.基于感应电机启动电磁转矩Hilbert-Huang变换的转子断条故障诊断［J］.中国电机工程学报，2005，25(11):107 －112.

［8］常军，张启伟，孙利民.稳定图方法在随机子空间识别模态参数中的应用［J］.工程力学，2007，24(2):39－44.

［9］李天云，袁明哲，蔡国伟，等.基于随机子空间和最小二乘法的介质损耗角检测方法［J］.高电压技术，2010，34(5):828 －833.

［10］周帮友，胡绍全，杜强.特征系统实现算法中的模型定阶方法研究［J］.科学技术与工程，2009，9(10):2715－2722.

［11］李楠，赵妍，李天云，等.基于随机共振理论的异步电动机转子断条检测新方法［J］.电工技术学报，2006，21(5):99－103.

［12］张莲，余成波，郑有根，等.异步电动机故障实时在线监测系统的研制［J］.压电与声光，2007(4):475－477.