大型锻造操作机提升机构运动分析及优化

王勇勤，杨青松，严兴春，韩炳涛，张营杰，房志远

(1.重庆大学机械传动国家重点实验室，重庆 400030;2.中国重型机械研究院，西安 721000)

锻造操作机用来配备0.5 t以上各种自由锻造压机，主要完成工件的升降、水平送进、回转、俯仰等运动［1］。锻造操作机与锻造加工设备协调作业，可以大大提高制造能力、制造精度、生产效率和材料利用率，降低能耗。赵凯等［2］针对自由锻造操作机建立多领域的耦合模型，进行了顺应运动的分析。杨文玉等［3］基于操作机性能指标对运动学参数进行评价，提供了一种性能优化和评价方法。任云鹏等［4］采用虚拟样机技术对操作机进行运动学仿真，得到了钳头的运动曲线。童幸等［5］建立了3种常见的锻造操作机的运动学模型，对操作机的主运动机构进行了解耦性研究。还有一些研究者运用解析法进行了操作机机构运动学分析［6－8］。但是锻造操作机作为一种重载操作设备，设计制造成本比较高，目前对于锻造操作机机构运动优化方面的研究还比较少。

1 操作机运动学分析

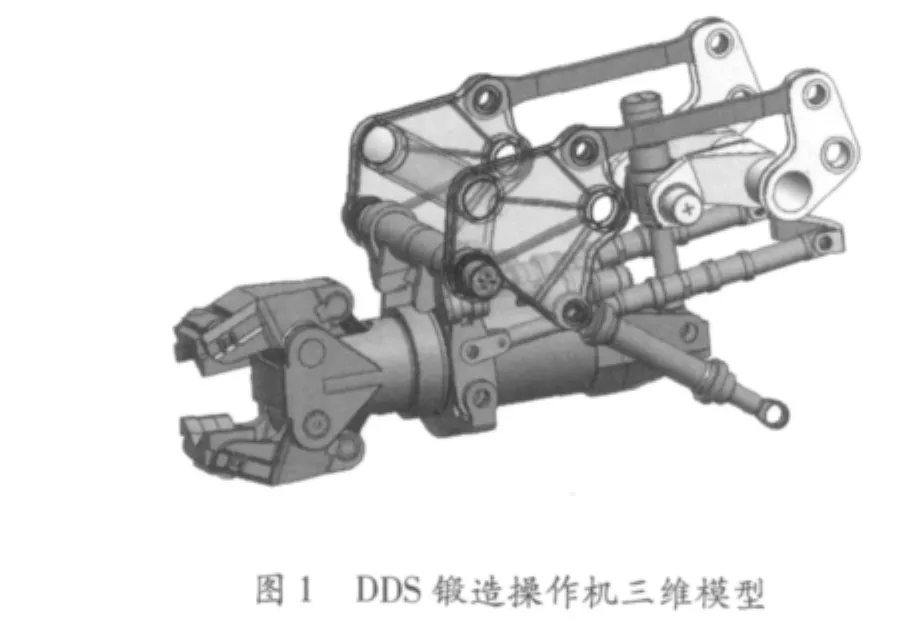
DDS锻造操作机的结构如图1所示。其吊挂机构可等效为对称布置的2个平行机构来进行分析，如图2所示。锻造操作机工作过程中要实现钳杆升降、钳杆倾斜以及缓冲3个基本动作。

本文主要针对钳杆升降运动的位置进行正解建模，即分析提升过程中提升缸的运动变化对夹钳末端运动的影响，运动学分析机构简图如图3所示。从图3中取出前转臂与提升缸机构，如图4所示，分别以三角形FKL和三角形IJL作为研究对象，I、L点的坐标为

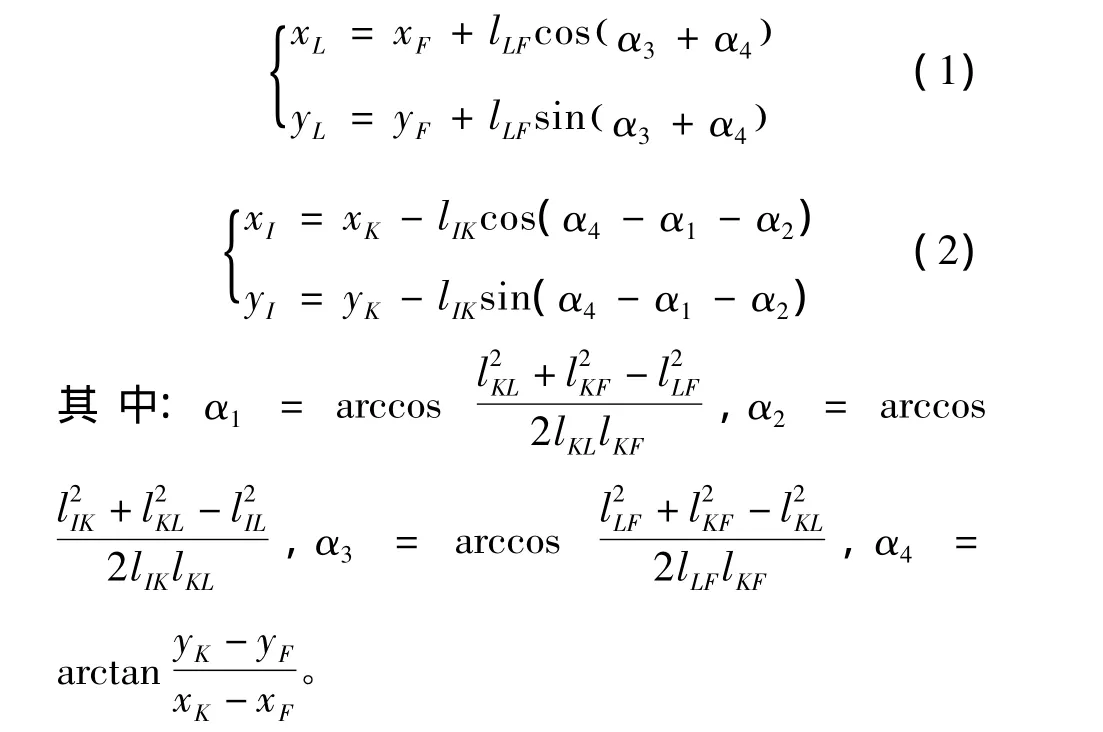
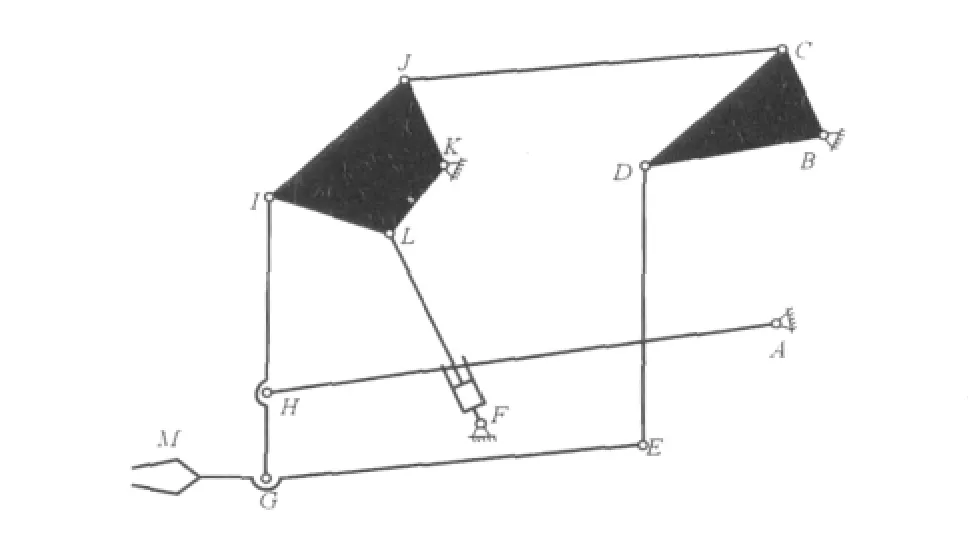
图3 操作机提升机构运动学分析简图

从图3中取出后转臂与连杆组成的机构，如图5所示，则H点和G点坐标为

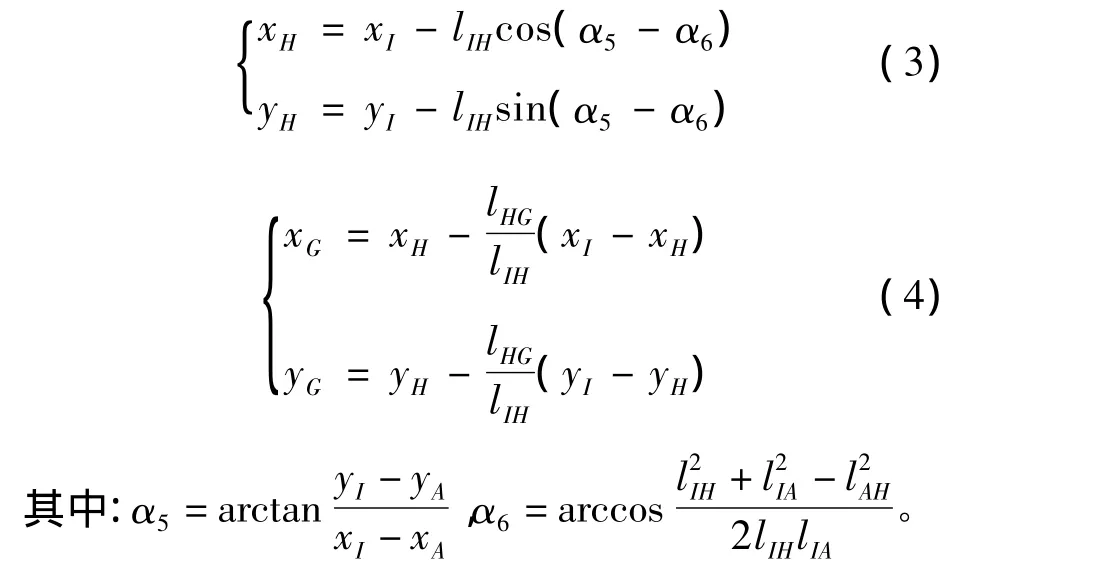
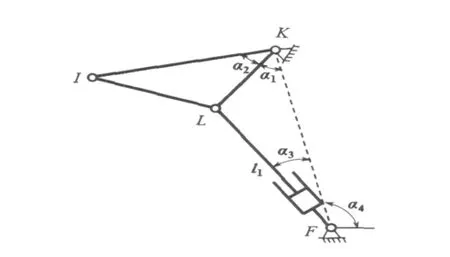
图4 前转臂与提升缸组成的机构

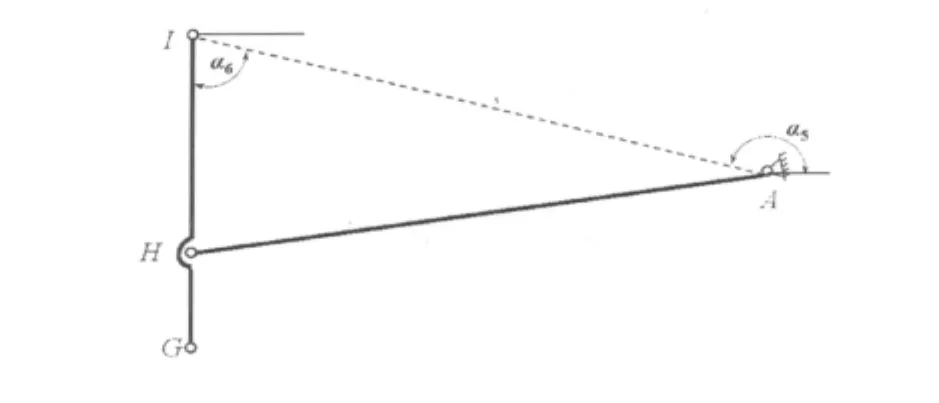
图5 前吊臂与缓冲缸组成的机构

2 提升机构优化模型的建立及求解

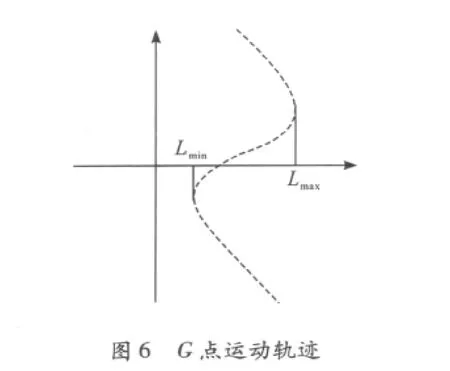
在操作机钳杆提升过程中，为保证提升精度，要求夹钳在水平方向的误差尽可能小，即如图6中G点应该尽可能作竖直方向的直线运动。因此，合理选择提升机构中各杆件的长度及安装尺寸就显得尤为重要。从图7不难看出，影响G点运动轨迹的主要因素应为缓冲缸与前吊臂铰接点位置H和杆长LHA及安装位置。鉴于此，本文采用数值优化方法对其展开研究，设计变量为图7中的A点坐标(xA，yA)以及杆IH的长度LIH，目标函数设定为G点水平方向运动误差最小，即

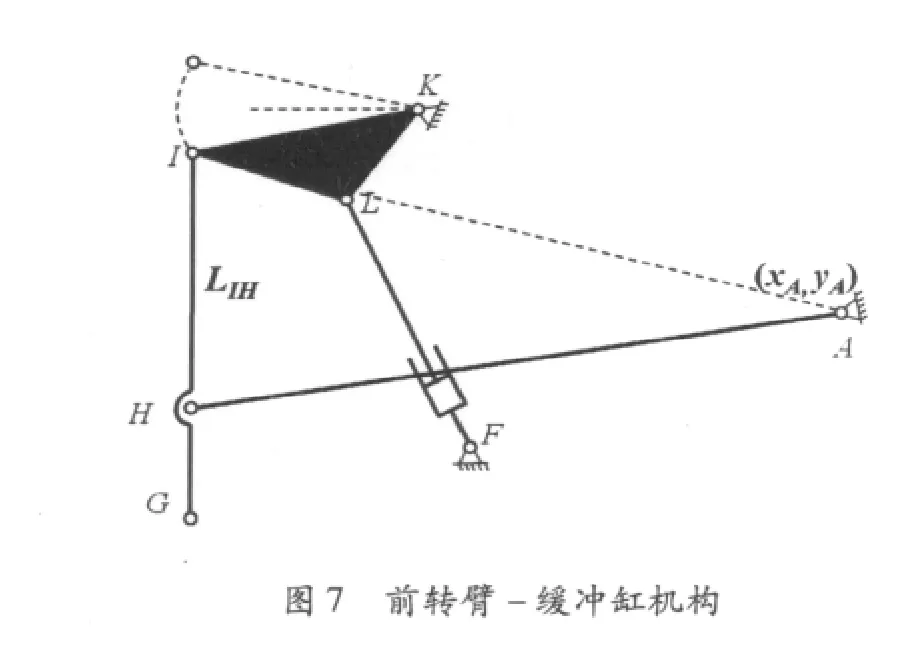
就约束条件而言，首先，在寻优过程中，A点横坐标不允许超过图2中B点横坐标，否则A点就会超出机架范围之外;其次，在LF变化过程中，三角形IHA必须存在，即边界条件为

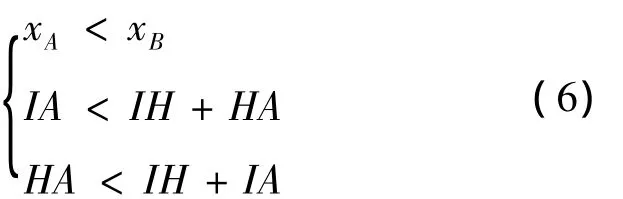
缓冲缸与前吊臂铰接点位置优化问题是有约束线性规划问题。随着各种计算方法的发展，各种优秀的计算软件相应诞生，其中Matlab以其强大而有效的优化方法受到广泛欢迎。本文调用Matlab优化工具箱的Fmincon函数进行优化设计。Fmincon优化函数首先检查用户是否直接提供了Hessian矩阵计算公式，如果提供，则直接计算Hessian矩阵，选择Large.Scale算法;否则检查是否直接提供目标函数的梯度，如果提供了也选择Large.Scale算法，由已提供了梯度的公式直接通过有限差分计算Hessian矩阵;如果没有提供Hessian矩阵计算公式和梯度表达式，Fmincon选择SQP算法，算法中Hessian矩阵可以通过DFP迭代，初始 Hessian阵任意给定。详细流程如图8所示。

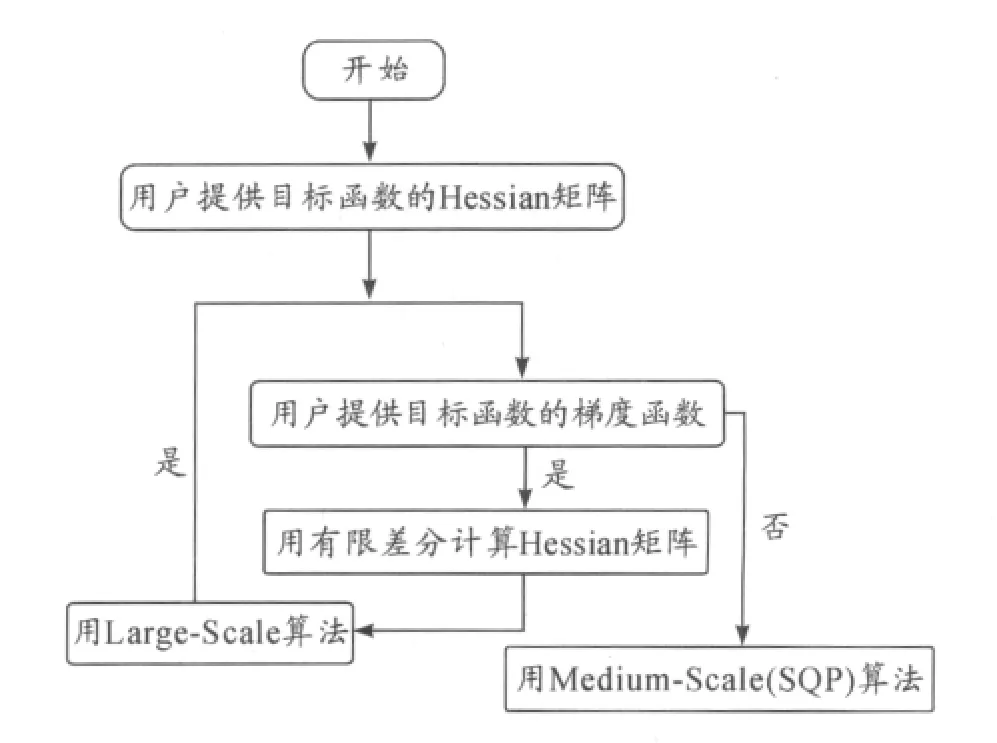
图8 Fmincon函数算法流程

3 优化结果分析

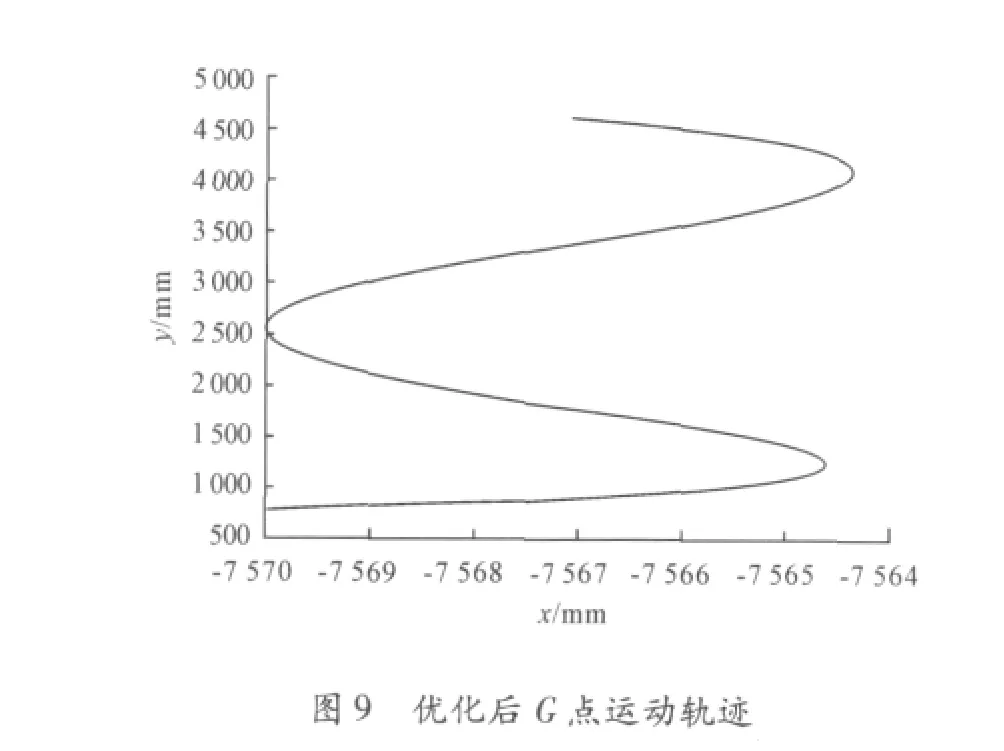
经优化计算后，A点坐标为(2002，3877)，杆HG长度为1218 mm，G点水平方向运动误差为5.9 mm，如图9所示。为了对比分析优化效果，现按照表1所示几种情况仿真G点水平方向运动误差，仿真结果如图10所示，对比分析研究发现:A点纵坐标比横坐标值对G点水平方向运动误差影响较大，杆HG的长度对其影响也较明显。

表1 寻优结果对比

4 结束语

通过数值优化方法对大型DDS锻造操作机提升机构进行了运动学分析与优化设计，得到了使提升机构在升降过程中水平方向运动误差为最小的最优解。通过对比分析优化结果与其他工况仿真结果，发现优化结果具有明显的优越性。该优化方法和模型对于锻造操作机提升机构的设计有一定的指导意义。

［1］中国机械工程学会塑性工程学会.锻压手册［K］.3版.北京:机械工业出版社，2008.

［2］赵凯，王皓，陈关龙，等.自由锻造操作机顺应过程分析［J］.机械工程学报，2010，46(4):27 －34.

［3］杨文玉，孟富明.锻造操作机顺应性能评价与优化方法［J］.机械工程学报，2010，46(23):121 －127.

［4］任云鹏，张天侠，陈希红，等.基于虚拟样机技术的万吨压机锻造操作机的运动学仿真分析［J］.工程设计学报，2008，15(2):101 －104.

［5］童幸，高峰，张勇.操作机主运动机构的解耦性研究［J］.机械工程学报，2010，46(11):14 －20.

［6］王怀彬.锻造操作机运动学与逆动力学分析［D］.上海:上海交通大学，2008.

［7］陈博翁.一种锻造操作机的机构分析及其虚拟样机建模［D］.北京:清华大学，2009.

［8］Yan C，Gao F，Guo W.Coordinated kinematic modelling for motion planning of heavy-duty manipulators in an integrated open-die forging centre［J］.2009(1):54 －58.

［9］Bela l.Sandor，Karen J.Richter.Engineering Mechanics Statics and Dynamics［M］.Englewood Cliffs:N.J.Prentice-Hall，2008.

［10］褚洪生，杜增吉，阎金华.MATLAB7.2优化设计实例指导教程［M］.北京:机械工业出版社，2007.

［11］贾振平.带壳体从动锥齿轮煅件的工艺分析及探讨［J］.重庆理工大学学报:自然科学版，2010(12):134－137.