微电极测井的三维有限元数值模拟
2012-09-18南泽宇范晓敏宋瑛士张意
南泽宇,范晓敏,宋瑛士,张意
(1.吉林大学地球探测科学与技术学院,吉林 长春 130026;2.中国石化石油勘探开发研究院,北京 100083;3.吉林大学白求恩第一医院,吉林 长春 130026)
0 引 言
采用三维有限元法模拟了微电极测井仪和井眼、泥饼、侵入带中的电场分布情况。由于模拟实际环境耗资巨大,而解析法又不能完成对复杂环境下场分布的计算,数值模拟成为多数地球物理学家的有力武器[1]。有限元法和有限差分法是解决电磁场问题的2种常用数值解法。有限元法和有限差分法先对求解域做网格剖分,进而用有限个网格节点代替连续的区间,然后将微分算子离散化,化微分方程的定解问题为大型线性方程组的求解问题[2]。微电极测井仪模型尺寸变化大,极板上的电极尺寸是毫米级,而原状地层和上下层的围岩厚度达数米,并且屏蔽极板尺寸不规则,这些因素使该区域的网格剖分有很大难度。但是有限元中的网格单元能按不同的连接方式进行组合,单元本身又可以有不同形状,因此有限元法比有限差分法更适合微电极这种几何形状比较复杂的求解域的离散化,进而完成井中电场分布的计算。
泥浆滤液侵入渗透性地层形成的泥饼影响储层评价精细度,为估算地层和侵入带真电阻率,进而为评价提供较可靠的依据,有必要研究泥饼对测井结果的影响。李大潜等[3]用有限元素法模拟微球形聚焦测井仪在二维电磁场中的效果;董建刚[2]用三维有限元法模拟微球形聚焦测井井中电场分布;康彤等[4]运用有限元程序自动生成系统(FEPG 3.0)模拟微球形聚焦测井在三维静电场中效果。前人的这些工作定量研究了微球形聚焦测井受泥饼和过渡带的影响,但是由于微电极测井的三维正演计算量大,其相应的定量研究工作较少,致使微电极系响应随泥饼厚度变化,电阻率变化的精细特征有待确定。本文试图在这方面开展研究工作,以便更好地定量认识微电极测井的响应特征,让微电极测井在渗透性储层评价中发挥更大的作用。
1 微电极系模型及电场分布
为了模拟微电极测井仪的电场分布,建立了低电阻率泥岩(10Ω·m)中存在高电阻率渗透性砂岩层(30Ω·m)时的三维有限元模型。钻井液电阻率设为0.1Ω·m,泥饼电阻率设为0.3Ω·m,侵入带电阻率为3Ω·m。高电阻率砂岩层厚0.5m,井眼直径为0.24m,泥饼厚度为0.005m,侵入带半径为0.625m。模拟了普遍使用的电极距=0.05 m的A0.05M微电位电极系和电极距AO=0.0375m的A0.025M10.025M2微梯度电极系。用四面体单元和三角形单元对该求解域进行离散,最小网格出现在泥饼和电极接触处,网格最短边为0.05 mm,最大网格出现在泥岩层的顶底面处,网格最长边为2.4m。在该求解域内电场遵循方程
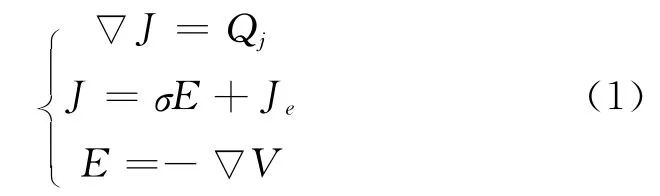
经计算发现供电电极A发出的电流在绝缘极板的屏蔽作用下进入泥饼,电流进入泥饼后发散开来,由于泥饼电阻率低于侵入带电阻率,大部分电流通过泥饼绕过屏蔽电极后流回井眼,部分电流穿过泥饼进入侵入带绕过屏蔽极板后经泥饼流回井眼。电流分布见图1。

图1 井中电流分布示意图
由于微电极系的测量结果受泥饼、侵入带、原状地层、极板形状等诸多因素影响,测量的电阻率为视电阻率[5],可通过式(2)计算

式中,Ra为视电阻率;K为装置系数,可以通过把周围介质设为各项同性均一介质计算,本文中K为0.4156m(微电位)或0.3357m(微梯度);V 为测量电极M2电位(微电位)或测量电极M1M2电位差(微梯度);I为供电电极A的电流值。
2 低电阻率泥饼存在时的微电极测井响应曲线
以往获得的微电极测井曲线多为实测曲线(受测量环境影响),或者是忽略了泥饼和侵入带、极板尺寸影响的解析解,这些曲线不能定量反映泥饼厚度以及电阻率变化对微电极测井曲线带来的影响。本文用三维有限元法精确计算了低电阻率泥浆(0.1 Ω·m)侵入时,低电阻率泥岩(10Ω·m)中存在高电阻率渗透性砂岩层(30Ω·m)时的微电极曲线。其中侵入带电阻率为3Ω·m,泥饼电阻率为0.3Ω·m,厚度为0.005m。计算结果见图2。
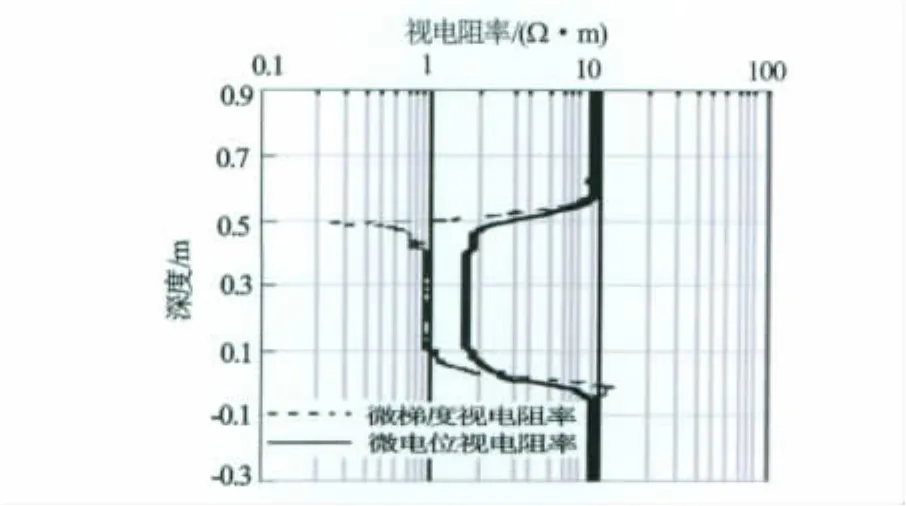
图2 低电阻率泥浆侵入时微电极测井对高电阻率层的响应
由于微梯度电极系的探测半径约等于它的长度,微电位电极系的探测半径等于其电极距的2倍。微电位电极系相对于微梯度电极系探测深度大,受泥饼的影响较小,所以当低电阻率泥饼存在时出现了微电位高于微梯度的正幅度差。可见利用微电极测井曲线可以判断泥饼的存在,进而判断岩层的渗透性[6]。
3 微电极测井曲线与泥饼厚度的关系
为定量了解微电极测井曲线与泥饼厚度的关系,建立了泥饼厚度在0.001~5cm变化的模型,并计算了相应的微电极测井响应。模型中泥饼电阻率为0.3Ω·m,侵入带电阻率为Ω·m,原状地层电阻率为30Ω·m。当泥饼厚度变化时,微电位、微梯度测井响应见图3;微电位、微梯度幅度差变化见图4。

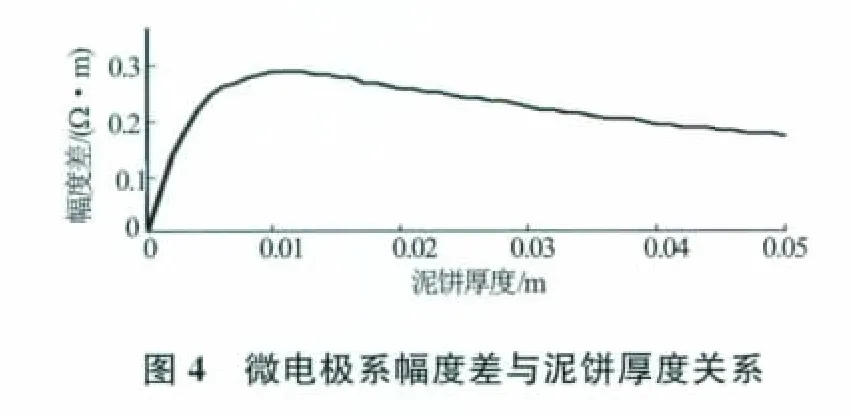
由图3可见,随泥饼厚度增大,微电极系测井曲线值迅速减小,微梯度测井曲线减小的速度大于微电位测井曲线减小的速度,从而出现正幅度差。当泥饼厚度达到一定值(3cm)时微电极系测井响应基本不随泥饼厚度的增加而变化。由图4可见微电极测井曲线的正幅度差并不是随泥饼厚度增大而一直增大的,当泥饼厚度小于1.08cm时,正幅度差随泥饼厚度迅速增大,在泥饼厚度为1.08cm处达到峰值,之后正幅度差随泥饼厚度的增大而逐渐减小。所以以往正幅度差越大,泥饼厚度越大,地层的渗透性越好的观点成立是有条件的,它不适用于泥饼厚度大于1.08cm的情况。
4 微电极测井曲线与泥饼电阻率的关系
为定量了解微电极系测井曲线与泥饼电阻率的关系,建立了泥饼电阻率0.01~10Ω·m变化时的模型,并计算了相应的微电极测井响应。模型中泥饼厚度为0.5cm,侵入带电阻率为3Ω·m,原状地层电阻率为30Ω·m。当泥饼电阻率变化时,微电位、微梯度测井响应变化见图5,微电极系幅度差变化见图6。

图5 微电极系视电阻率与泥饼电阻率的关系
由图5、图6可见,随泥饼电阻率增大,微电极和微梯度测井视电阻率均增大,当泥饼电阻率低于侵入带电阻率时,微电位电极系视电阻率高于微梯度电极系视电阻率,出现正幅度差。随泥饼电阻率继续增大并逐渐接近侵入带电阻率,幅度差逐渐减小。当泥饼电阻率与侵入带电阻率相等时,幅度差为。当泥饼电阻率高于侵入带电阻率时,微梯度电极系视电阻率大于微电位电极系,出现负幅度差。
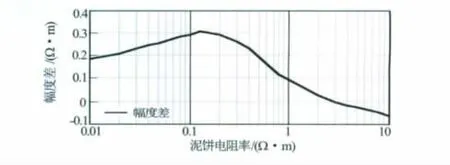
图6 微电极系幅度差与泥饼电阻率的关系
测井中一般通过钻头直径和实际井径之差计算泥饼厚度[7]

式中,hmc为泥饼厚度;d0为钻头直径,可以通过钻头程序查得;d为井径测井值。如已知泥饼厚度可以通过该泥饼厚度下的模拟微电位或微梯度视电阻率与泥饼电阻率关系曲线,精确确定泥饼电阻率。
5 结 论
(1)通过三维有限元法模拟了微电极测井仪的仪器结构和存在泥饼侵入带时的井中环境,计算了井中的电场分布。相对于以往用解析法计算的微电极测井曲线更全面地考虑了泥饼厚度、电阻率等因素对微电极测井曲线的影响,为今后精细研究微电极测井曲线,进而划分薄互层、确定储层中的钙层,泥岩夹层厚度奠定了理论基础。
(2)定量计算了微电位、微梯度测井曲线及两者之间的幅度差与泥饼厚度的关系。发现当泥饼厚度为1.08cm时,现在生产中普遍采用的微电极系测井仪的幅度差达到最大值。当泥饼厚度大于此值时,随泥饼厚度的增大,微电极系幅度差有缓慢减小的趋势。即微电极系幅度差越大,地层渗透性越好,这一规律的适用条件为泥饼厚度小于1.08cm。
(3)模拟了微电极测井曲线随泥饼电阻率变化的关系,在已知钻头程序和井径曲线的情况下可以精确确定泥饼的电阻率值。准确求取泥饼电阻率对测井曲线的环境校正具有重要意义。
[1]LIN Jiayong,DING Maobin,TANG Jingtian,et al.Study of Numerical Simulation on Dual-frequency IP Method with FEM[J].Global Geology,2010,13(2):99-103.
[2]董建刚.微球形聚焦测井有限元模拟[D].长春:吉林大学,2007.
[3]李大潜,郑宋穆,谭永基,等.有限元素法在电法测井中的应用[M].北京:石油工业出版社,1980:171-176.
[4]康彤,梁国平,窦海勇.微球形聚焦测井中三维电场模型有限元法的数值模拟[J].北京广播学院学报:自然科学版,2002,3:7-10.
[5]李舟波.钻井地球物理勘探[M].北京:地质出版社,2005:26.
[6]李舟波.地球物理测井数据处理与综合解释[M].北京:地质出版社,2007:104-116.
[7]田志杰.测井资料环境校正、标准化处理程序设计与实现[D].北京:中国地质大学,2007.
