基于ANSYS软件的随钻电磁波测井正演模拟计算
2012-09-18丁晓林林春丹邵长金
丁晓林,林春丹,邵长金
(中国石油大学,北京 102249)
0 引 言
随钻测井技术正在迅速发展。王华等[1]论述了随钻声波测井的纵波测量、横波测量及仪器的发展,分析了随钻声波测井面临的难题和进展。随钻电磁波测井可以在泥浆侵入前测量地层真实电阻率,为钻井和地质导向提供有价值的信息。杨震等[2]为了研究随钻电磁波在复杂测井环境中的响应规律,从Maxwell电磁响应方程出发,针对大斜度井井眼和侵入剖面的几何特点,采用新的网格划分方法,并应用基于交错网格的有限差分得到了三维频率域电磁响应差分计算格式,采用改进的ICCG(不完全乔尔斯基共轭梯度)方法,对一维变带宽存储的大型复稀疏矩阵进行了求解,得到了随钻电磁波测井响应。王滨涛等[3-4]在理论上研究了随钻电磁波电阻率测井视电阻率提取及正演的数值模拟方法和视电阻率转换方法。孙向阳等[5-6]用矢量有限元研究了随钻测井的三维电磁响应数值模拟方法。他们的研究模型比较简单,无法适应实际地质情况,特别是水平井和大斜度井情况下随钻测井在各向异性地层中的数值模拟还有待深入,本文用ANSYS有限元软件对随钻电磁波测井在各向同性地层和各向异性地层进行了比较,对钻铤及地层各向异性因素在倾斜井眼中电磁响应进行了研究。
1 随钻电磁波测井响应计算原理
在随钻电磁波测井仪(见图1)中,当线圈半径远远小于发射线圈与接收线圈之间的距离时,可把线圈近似为磁偶极子。
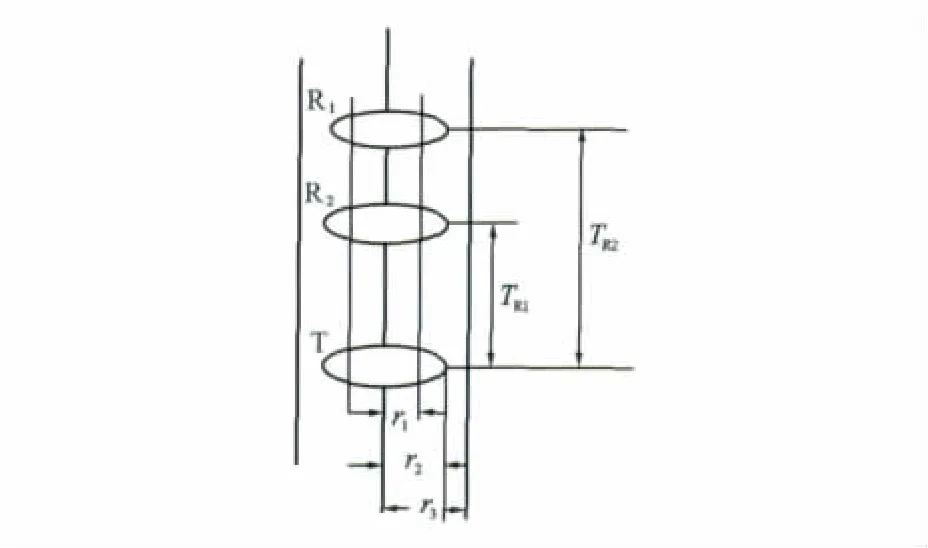
图1 随钻电磁波测井仪计算模型
设均匀介质中有半径为aT,匝数为nT的发射线圈,其中通以交变电流IT=I0eiωt,则介质中电场强度所满足的微分方程为非齐次的Helmholtz方程[4]

式中,k2=-ωμ(σ+iωε);ω 为电流角频率;μ为介质的磁导率;ε为介电常数;σ为电导率;JT为发射线圈电流密度。k称为传播常数k=α+iβ,且
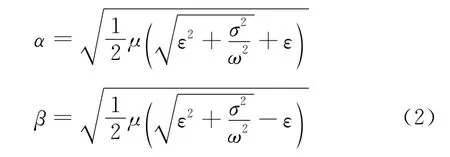
在均匀介质中,式(1)的解可表达为

式中,R′是场点到电流元的距离。由于电磁波传播的空间范围远大于线圈的尺寸,上述积分可表示为面积分与线积分之积,得到
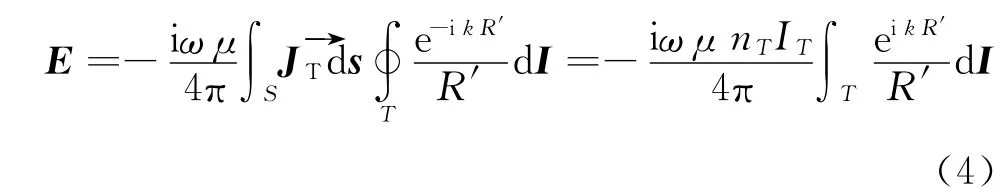
设线圈中心为圆柱坐标系的原点,线圈平面垂直于z轴。P(r,z)为空间中任一点,该点的电场强度E关于z轴对称,只有Φ分量,因此

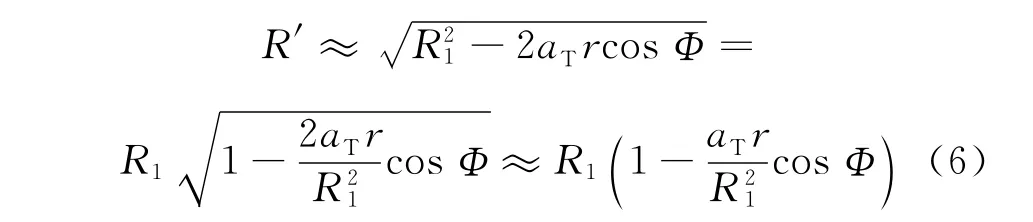
将式(6)代入式(5)积分得
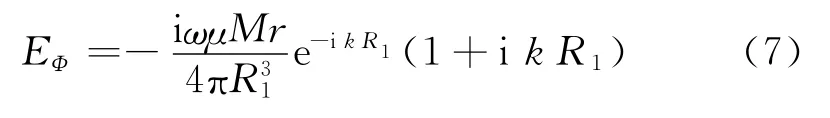
式中,M为磁偶极距,M=nTSTIT;ST是发射线圈的面积,ST=。
若发射线圈T与接收线圈R(半径aR,匝数nR)距离为L,式(7)中,以L代替R1(因为aR远远小于L),则接收线圈的感应电动势为

式中,SR是接收线圈的面积,SR=。
将k=α+iβ代入式(8),则接收线圈R1和R2的感应电动势可以表示为

把式(10)代入式(1),得到2个接收线圈感应电动势的幅度衰减EATT和相位差ΔΦ,
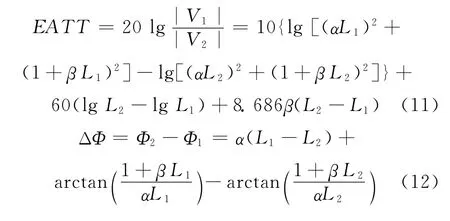
2 数值模拟
图1计算模型的参数,钻铤[5]半径r1=0.1016 m,线圈半径r2=0.1270m,井眼半径r3=0.1524m,线圈距TR1=0.3048m,TR2=0.4572m,绕钻铤线圈匝数nT=120,nR1=nR2=180,钻铤的长度LZ=1.0m,线圈长度LX=0.0568m,频率为400kHz和2MHz,频率取值主要考虑了对地层电阻率的敏感性,而对介电常数则相对不那么敏感,统一把相对介电常数设为10,计算地层视电阻率[6]。基于前人的工作,本文采用由接收线圈的相位差得到的相位差视电阻率,使用ANSYS软件进行计算和分析。
2.1 验证模型正确性
根据基本原理,在400kHz和2MHz频率时,测井数据主要对地层电阻率敏感,对介电常数不敏感,采用相位差刻度,所以测得的是相位差视电阻率曲线。表1给出均匀地层模型下磁偶极子理论解和数值解的对照数据,可以看出所建立的模型基本满足原理要求。一旦知道了相位差,就可以根据图2进行相位差-视电阻率曲线线性插值,从而求得视电阻率。
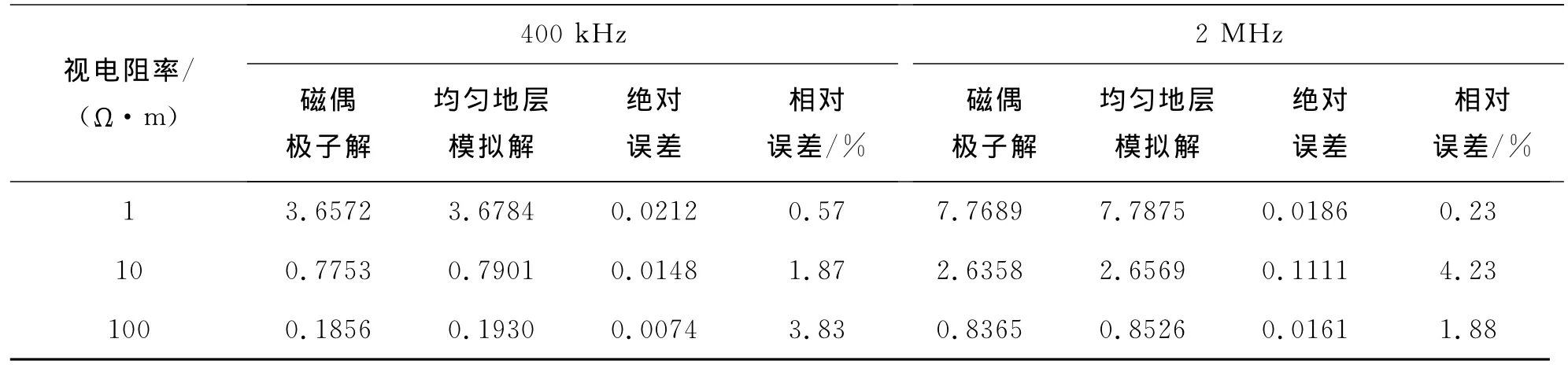
表1 均匀地层模型下磁偶极子理论解和数值解对照表
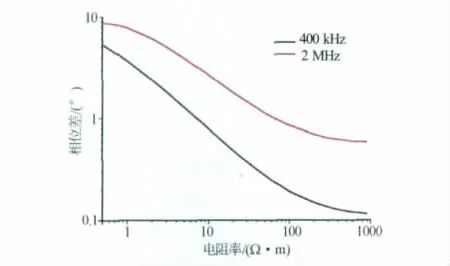
图2 均匀地层相位差刻度视电阻率曲线线性插值图
2.23 层对称地层模型正演模拟
本文主要模拟3层地层情况,模型的上下围岩对称,中间为地层,分别考虑高围岩、低围岩时相应因素对电阻率的影响。
2.2.1 钻铤因素的影响
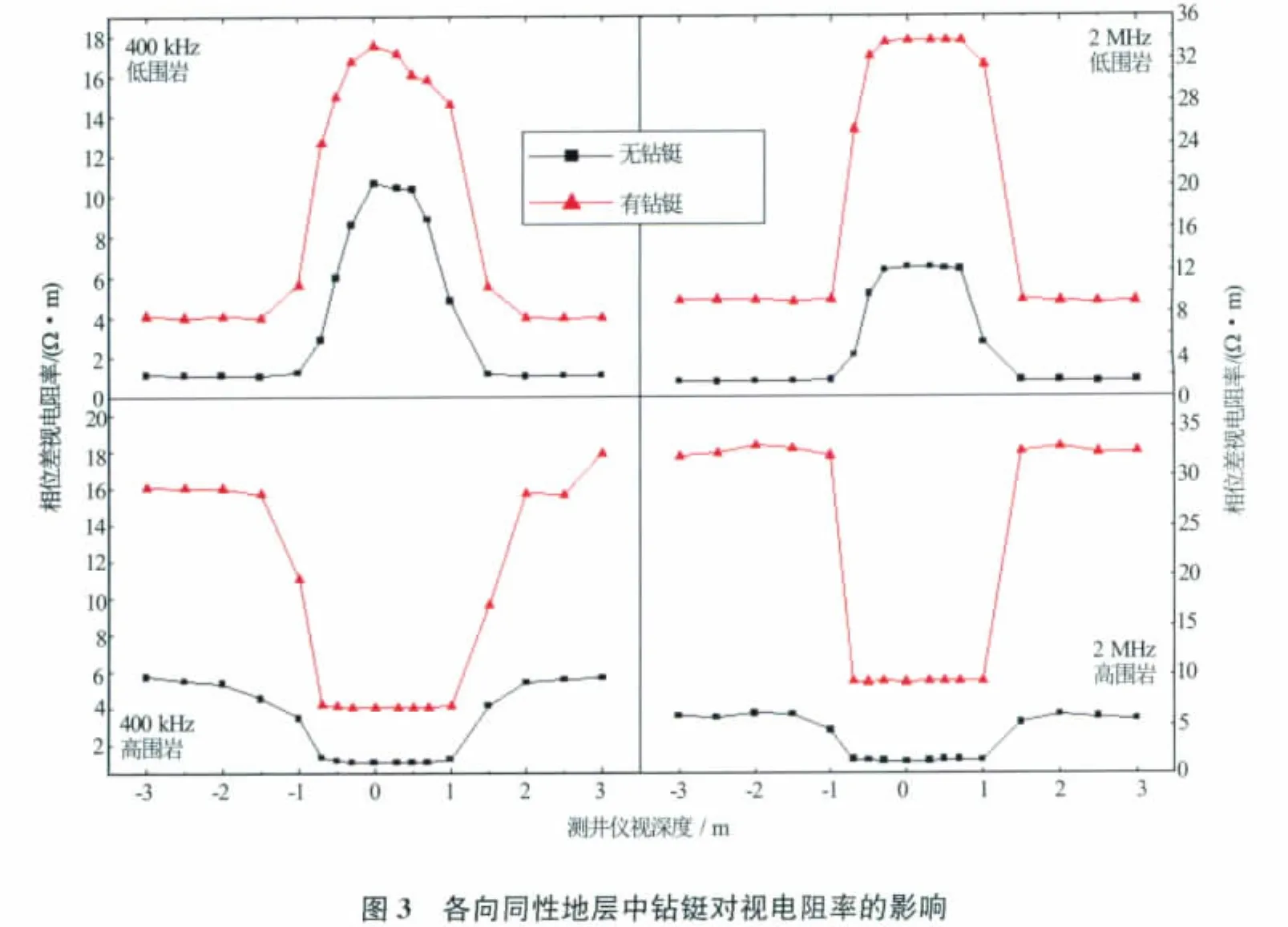
在各向同性介质情况下,分低围岩和高围岩2种情况进行讨论。低围岩时,取地层电阻率为10Ω·m,围岩电阻率为1Ω·m;高围岩时,取地层电阻率为1Ω·m,围岩电阻率为10Ω·m。分别在400kHz和2MHz这2种频率下,得到有钻铤和无钻铤时相位差视电阻率曲线(见图3)。
由图3可以看出,低围岩时曲线要比高围岩时曲线更加接近地层真实电阻率值,说明相位差刻度曲线受高围岩影响较大;有钻铤时相位差刻度视电阻率值要普遍大于无钻铤时相位差刻度视电阻率值,说明钻铤的存在对相位差视电阻率值有一定影响,但是曲线变化规律没有受到影响;而且频率不同,钻铤对相位差刻度视电阻率值的影响也不同。图3中有钻铤与无钻铤对相位差刻度视电阻率值的影响,2MHz情况下要比400kHz情况下差别更大。
上述结果说明,随钻测井钻铤的存在对测井曲线产生的影响不改变曲线的大致走向,对测井过程中油层的辨别及边界面的界定影响不大,但是对反演地层参数有一定影响,所以需要根据实际测井制作反演校正图版。
2.2.2 介质各向异性的影响
为说明介质各向异性的影响,在其他相同条件下,将各向同性介质与各向异性介质情况下的结果进行对比。各向同性介质计算参数,低围岩时设地层电阻率为10Ω·m,围岩电阻率为1Ω·m,高围岩时相反。各向异性介质计算参数低围岩时设地层横向电阻率为10Ω·m,纵向电阻率为2.5Ω·m,围岩横向电阻率为1Ω·m,纵向电阻率为0.25Ω·m(横向电阻率是纵向电阻率的4倍),高围岩时相反。所得到的相位差视电阻率曲线变化见图4。

由图4可以看出,对于2种频率,无论低围岩还是高围岩地层,各向同性介质相位差刻度视电阻率都要大于各向异性介质相位差刻度视电阻率;无论低围岩或者高围岩,有钻铤时各向同性介质与各向异性介质之间的差别小于无钻铤时情况。
上述结果说明,随钻测量中各向同性地层与各向异性地层测井数据是不同的,反映在倾斜井眼中较为明显,因为随着倾斜角的增大,越来越多的受到垂直方向的地层电阻率的影响。
2.2.3 倾斜地层的影响
分别在各向同性介质和各向异性介质中研究了倾斜井眼的影响。取井眼倾斜角度分别为0°、15°、30°、45°、60°和75°(见图5)。对各向同性介质,计算参数为低围岩时设地层电阻率为10Ω·m,围岩电阻率为1Ω·m,高围岩时相反。对各向异性介质,计算参数为,低围岩时设地层横向电阻率为10Ω·m,纵向电阻率为2.5Ω·m,围岩横向电阻率为1Ω·m,纵向电阻率为0.25Ω·m,横向电阻率是纵向电阻率的4倍,高围岩时相反。相位差视电阻率曲线变化见图6至图8。

图5 倾斜井眼地层模型
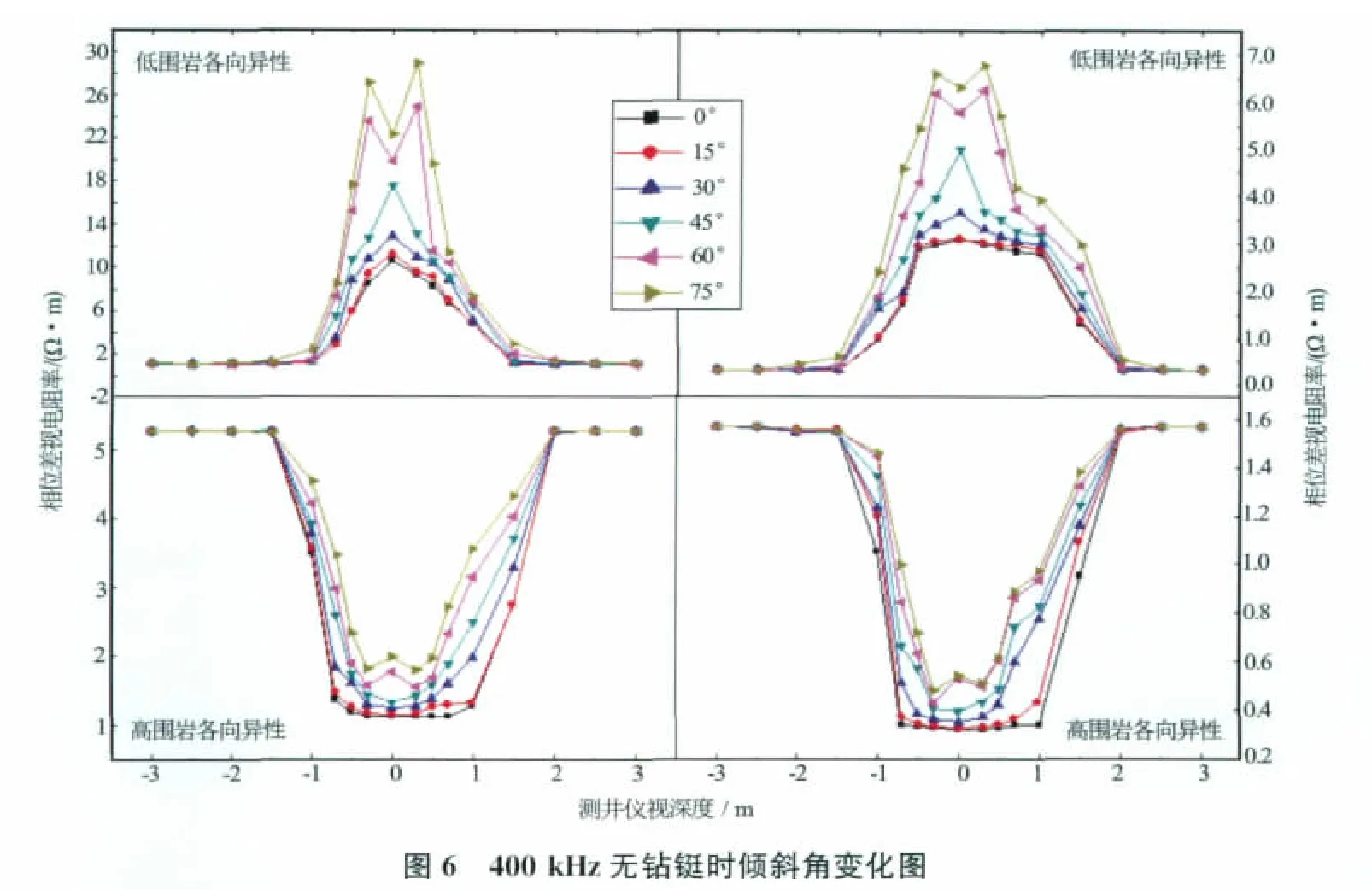
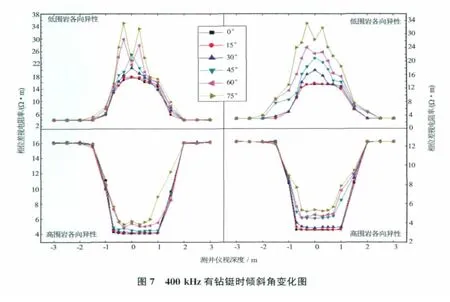
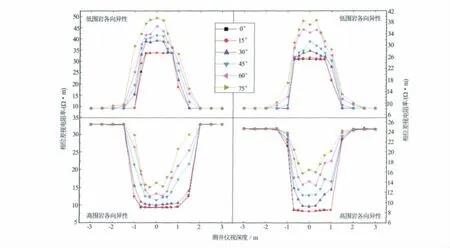
图8 2MHz有钻铤时倾斜角变化图
由图6至图8可以看出,0°~15°倾斜角范围内的地层视电阻率曲线基本重合,说明小角度倾斜井和竖直井差别不大,可以近似使用竖直井反演校正图版。但随着倾斜角的继续增大,视电阻率曲线愈加陡峭,也愈加偏离地层真实相位差刻度电阻率值。无论高围岩或低围岩,在地层视深度范围内,随着井眼倾斜角度增加,相位差视电阻率值变大,并在围岩与地层的边界处曲线不再平滑且出现犄角。当角度大于60°时,这种曲线犄角变形加重,越偏离地层真实电阻率值,可见大斜度井对测井曲线的影响很大。
上述结果说明,对倾斜井眼,倾斜角度的增大,曲线也越偏离地层真实电阻率值,说明传统测井解释图版已经不能适用于现在越来越多的大斜度井反演解释,急需基于实际的大斜度井反演解释图版。
3 结论与讨论
(1)随钻电磁波测井钻铤的存在对测井曲线产生的影响不改变曲线的大致走向,对测井过程中油层的辨别及边界面的界定影响不大,但是对反演地层参数有一定影响,所以需要根据实际测井制作反演校正图版。
(2)随钻电磁波测井中各向同性地层与各向异性地层测井数据是不同的,反映在倾斜井眼中较为明显,因为随着倾斜角的增大,越来越多的受到垂直方向的地层电阻率的影响。
(3)对倾斜井眼,倾斜角度的增大,曲线也越偏离地层真实电阻率值,说明传统测井解释图版已经不能适用于现代越来越多的大斜度井反演解释,急需基于实际的大斜度井反演解释图版。
[1]王华,陶果,张绪健.随钻声波测井研究进展[J].测井技术,2009,33(3):197-203.
[2]杨震,范宜仁,文艺,等.三维频率域随钻电磁波测井数值模拟[J].地球物理学进展,2009,24(5):1833-1838.
[3]王滨涛,吴锡令,苑娜,等.随钻电磁波电阻率测井视电阻率提取及正演模拟分析[J].科学技术与工程,2010,10(13):3050-3053.
[4]高杰,辛秀艳,陈文辉,等.随钻电磁波电阻率测井之电阻率转化方法与研究[J].测井技术,2008,32(6):503-507.
[5]孙向阳,聂在平,李爱勇,等.用高阶叠层矢量有限元法计算随钻测井的三维电磁响应[J].电波科学学报,2009,24(2):1-7.
[6]孙向阳,聂在平,赵延文,等.用矢量有限元方法模拟随钻测井仪在倾斜各向异性地层中的电磁响应[J].地球物理学报,2008,51(5):1600-1607.
