基于ν－最大间隔超球体支持向量机的非平衡数据分类

李秋林

(西南大学数学与统计学院，重庆 400715)

经典的支持向量机(SVM)［1］通过构造最优超平面来分隔两类样本，由于其简单和良好的泛化能力使得其在众多领域得到广泛应用［2－8］。Tax和 Duin［9－10］受支持向量机的启发，提出了超球体支持向量机(HSSVM)，用于支持向量数据描述分类，其主要思想是建立包含样本的最小超球体。HSSVM已广泛应用于人脸识别、预警技术、故障检测等方面。在此基础上，有学者相继提出了最大间隔最小体积球形支持向量机［11］、不等距超球体支持向量机［12］、最大边界模糊核超球分类方法［13］等。

非平衡数据集是指数据集中某些类的样本数量比其他类的样本数量大很多，其中样本少的类为少数类(称为正类)，样本多的类为多数类(称为负类)。非平衡数据集普遍存在于机器学习的许多实际应用领域中。利用传统的机器学习方法分类，对于正类来说分类精度很低，而对于负类则相对较高。若少数类别的数据有很大的分类代价，少数类样本被错误分类所带来的危害要比多数类样本被错误分类大得多。如何有效地提高分类器对非平衡数据集的分类性能是目前机器学习和模式识别领域的一个热点研究问题。本文通过直接采用最大化间隔，并引入参数ν来建立一种新的模型，称之为ν－最大间隔超球体支持向量机(ν－MMHSSVM)，即构造2个同心超球，并使其间隔最大，小超球将正类包裹其中，大超球将负类样本排除在外。实验仿真结果表明，该算法对非平衡数据集的分类效果明显好于传统的算法。

1 超球体支持向量机

对于超球体支持向量机(HSSVM)，以a为中心、R为半径的圆可以包含所有的样本点，并且要求这个圆尽可能地小。不失一般性，超球体算法为了解决非线性问题，通过核函数把训练样本映射到高维特征空间。设初始训练样本集合X={xi|xi∈RN，i=1，…，l}，则原始优化问题为:

其中 K(xi，xj)=(Φ(xi)，Φ(xj))。通过求解对偶问题(2)，最终可以得到判决函数为

其中x为支持向量。

2 ν－最大间隔超球体支持向量机

2.1 ν－最大间隔超球体支持向量机

HSSVM是通过构造最小超球半径为目标进行分类，因此，在处理非平衡数据集时容易降低正类分类准确率，从而导致其泛化能力有限，所以，本文以最大化间隔、最小化超球半径为目标来建立一种新的超球体SVM算法，并引入参数ν，用于调节间隔和超球半径，得到ν－最大间隔超球体支持向量机(ν－MMHSSVM)。如图1所示，记“+”正类样本为，记“－”负类样本为，正负类间间隔为ρ，得到2个同心超球S1和S2，其中:S1半径为R;S2半径为R+ρ。

图1 ν－最大间隔超球体支持向量机

建立的数学优化模型为:

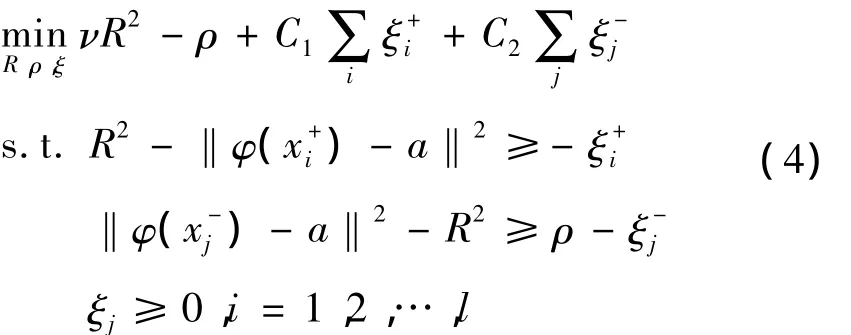
下面求解原始问题(4)的对偶问题，其Lagrange函数为:

其中α≥0，β≥0，为 Lagrange乘子向量。由 KKT条件可得:

通过求解式(12)，得到最优解α，代入式(8)可得超球球心。

由KKT条件得:

引入核函数，令 K(xi·xj)=(φ(xi)·φ(xj))，其间隔为ρ=‖φ()－a‖－‖φ()－a‖，并记，则原问题的判决规则为:对于测试样本 x，若‖x －a‖≤R1，记

则判定其为正类，反之判定其为负类。决策函数为

2.2 算法复杂度分析

算法复杂度由规划中变量和约束方程的个数决定。SVM、HSSVM、ν－MMHSSVM求解的都是凸二次规划问题。用Q(d，s)表示一个凸二次规划问题，CQ(d，s)表示对应的复杂度，其中d为变量个数，s为约束方程的个数。若训练样本数为n，则SVM、HSSVM、ν－MMHSSVM 算法的复杂度分别表示为 CQ(n，2n+1)、CQ(n，2n+1)、CQ(n，2n+2)。SVM在时间和空间上的复杂度为O(n2)［14］，即

令式(14)中的n取值n+1，则有

显然式(16)成立。

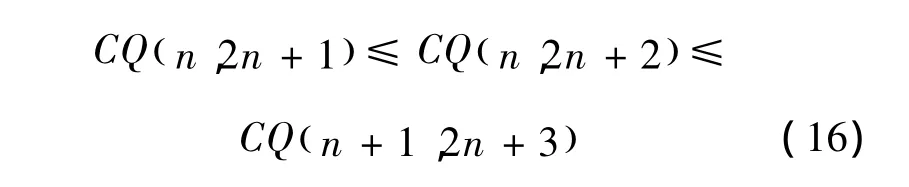
由式(14)～(16)可得 CQ(n，2n+2)=O(n2)，故各个算法复杂度同级。

3 实验仿真

3.1 人工数据集

先通过人造数据集来验证ν-MMHSSVM的有效性。随机产生容量为100的训练集，其中正类点5个，负类点各95个，这样就构造出了一组人工非平衡数据集。用ν-MMHSSVM进行训练，并调节参数ν来调节超球分割，分类结果见图2、3。

若正负类超球线性可分，从图2、3可知:参数ν越小，则包裹正类的超球半径就越大;参数ν越大，则包裹正类的超球半径就越小。故通过调节参数ν，就可以提高正类的分类准确率。

图2 ν=0.5时最大间隔超球体支持向量机

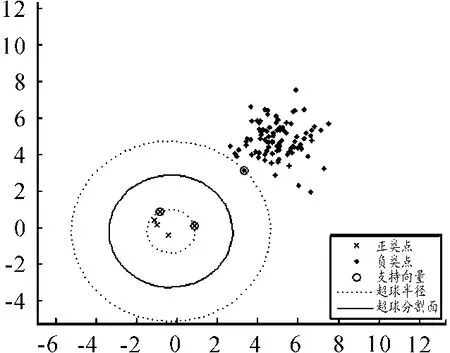
图3 ν=5时最大间隔超球体支持向量机

若正负类超球线性不可分，通过核函数映射到高维空间超球可分，其参数ν的变化、超球分割面变化的情况与线性情形下类似，结果如图4、5所示。

图4 ν=0.5，σ=0.5时最大间隔超球体支持向量机

图5 ν=5，σ=0.5时最大间隔超球体支持向量机

从上面的模拟可知，随着参数ν的变化，ν－MMHSSVM对线性和非线性情况都进行了正确分类。

3.2 真实数据集

从UCI公共数据库中选取了5组数据集进行了实验。表1中列出了本次实验所用的数据。为了方便，这里的实验数据都是正样本数相对于负样本数极其稀少的情况。表1中对正负类的情况进行了标号，并给出了正负类各占整个数据集的比例情况，然后通过径向基核函数映射后，并采用HSSVM、MMHSSVM进行训练，最后给出训练对比的结果。

表1 实验中使用的数据集

3.2.1 评价标准

类准确率是评价模型分类器最常用的标准，它可以反映分类器对于数据集的整体分类性能。但是，它不能正确评价非均衡数据集的分类结果。例如，100个样本中，正类样本数为5，负类样本数为95。如果将所有样本分为负类样本，分类的正确度仍为95%，这个评价结果显然是不合理的，若此时正类分类代价较高，误判带来结果就比较严重。因此，对于非均衡数据集分类需要一个合理的评价标准。

对于本次实验，采用文献［16］中正负查全率(Recall)和g均值方法来评价实验结果:

其中:TP、TN表示正确分类的正类和负类;FN、FP错误分类的正类和负类;Recall+、Recall－表示2个类的查全率。

表2是不同算法对各个数据集的正负查全率，表3为不同算法对各个数据集的g均值及平均值。

表2 不同算法的分类精度

表3 不同数据集的g均值及平均值

从表2可以看出，HSSVM有较高的负查全率，且远高于正查全率，但正查全率较低。而ν－M MHSSVM不但有较高的正查全率，而且还有较高的负查全率。通过表3可以看出，ν－MMHSSVM的各个数据集上的g均值均高于HSSVM在各个数据集上的g均值，ν－MMHSSVM的g均值平均值也明显高于HSSVM的g均值平均值。

4 结束语

基于ν－MMHSSVM的非平衡数据分类既能提高正类的聚类性，也能保证正负类类间间隔的距离最大，进而提高了模型分类器的性能，且模型的算法复杂度与其他算法是同级的。通过上面的实验仿真可以得出结论:与传统的HSSVM算法相比，本文提出的ν－MMHSSVM分类算法大大提高了对正类的查全率，从而有效地提高了对非平衡数据集的分类性能。

［1］Vapnik V N.The Nature of Statistical Learning Theory［M］.London，UK:Springer-Verlag，1995.

［2］邬啸，魏延，吴瑕.基于混合核函数的支持向量机［J］.重庆理工大学学报:自然科学版，2011(10):66－70.

［3］余珺，郑先斌，张小海.基于多核优选的装备费用支持向量机预测法［J］.四川兵工学报，2011(6):118－119.

［4］万辉.一种基于最小二乘支持向量机的图像增强算法［J］.重庆理工大学学报:自然科学版，2011(6):53－57.

［5］罗沛清，梁青阳，江钦龙，等.基于分层聚类的支持向量机模拟电路故障诊断［J］.四川兵工学报，2011(9):92 －95..

［6］崔建国，李明，陈希成.基于支持向量机的飞行器健康诊断方法［J］.压电与声光，2009(2):266－269.

［7］张宏蕾，张立亭，罗亦泳，等.基于支持向量机的土地利用预警研究［J］.安徽农业科学，2010(35):20503－20504.

［8］唐晓芬，赵秉新.基于支持向量机的农村劳动力转移预测［J］.安徽农业科学，2011(11):6837－6838.

［9］Tax D，Duin R.Support vector domain description［J］.Pattern Recognition Letters，2003，20:11 －13.

［10］Tax D，Duin R.Support vector domain description［J］.Machine Leaning，2004(1):45 －66.

［11］文传军，詹永照，陈长军.最大间隔最小体积球形支持向量机［J］.控制与决策，2010，25(1):79 －83.

［12］张慧敏，柴毅.不等距超球体支持向量机［J］.计算机工程与应用，2011，47(11):19 －22.

［13］王娟，胡文军，王士同.最大边界模糊核超球分类方法［J］.计算机应用 2011，31(9):2542 －2545.

［14］Collobert R，Bengio S.SVMTorch:Support vector machine for large-scale regression problems［J］.J of Machine Learning Research，2001，1(2):143 － 160.

［15］Frank A.Asuncion A UCI repository of machine learning databases［EB/OL］.［2012 － 06 － 18］.http://archive.ics.uci.edu/ml.

［16］Joshi M V.On Evaluating Performance of Classifiers for Rare Classes［C］//Proc of the 2nd IEEE International Conference on Data Mining.Maebishi，Japan:［s.n.］，2002:641－644.