6－PSS并联机构误差标定方法

宋晓飞，石万凯，刘开友

(1.重庆大学机械传动国家重点实验室，重庆 400030;2.重庆市电力公司 教育培训中心，重庆 400053)

并联机构具有刚度大、精度高、承载能力强等优点，已经被广泛应用于工业、航空、航海、医疗等领域。为了提高并联机构的运动精度，国内外学者对各构型并联机构的误差分析及标定进行了相关研究。文献［1－2］分析了六自由度并联机构的误差，建立了运动学误差模型，但没有包括铰链间隙误差。文献［3］提出了一种用测距仪测量位置偏差，从而标定机构误差参数的方法，此方法不需要昂贵的测量仪器，但要求测距仪的安装与参考坐标轴相平行，这很难做到。文献［4－6］都是利用激光追踪仪测得机构末端位姿，从而对机构进行误差标定，但都没考虑铰链间隙误差的影响。文献［7］对并联机构铰链间隙误差标定进行了理论分析，但提出的方法无法实现铰链间隙的标定。

本文提出一种6－PSS并联机构误差标定方法，此方法可将杆长误差跟铰链间隙误差分离开来，从而提高误差标定的准确度，为进一步的误差补偿提供基础。

1 研究对象

6－PSS型六自由度并联机构由6根连杆通过上下球铰将上方4根导轨及下方的动平台连接起来，6－PSS型六自由度并联机构简图如图1所示。在静、动平台上分别建立固定坐标系oxyz和连体坐标系o1x1y1z1，从动平台坐标系o1x1y1z1到固定坐标系oxyz的旋转矩阵

图1 6－PSS六自由度并联机构简图

1.1 并联机构运动学方程

由图1知，根据杆长的关系，得到等式

其中Si和Bi分别表示上下铰链点在固定坐标系下的坐标向量。

滑块的运动参数可表示为机构尺度参数和动平台末端位姿参数的函数，即机构运动学方程:

1.2 误差项分析

6－PSS并联机构存在的主要误差项有滑块初始位置误差、杆长误差、上下铰链安装位置误差、导轨直线度误差、铰链间隙误差。

上述误差项中除了铰链间隙误差外，其余各项误差都是不随机构运动状态而改变的静态误差，而铰链间隙误差是随机构位姿变化而变化的。因此，将铰链间隙误差从各误差项中分离出来将会提高各误差项标定的准确性。

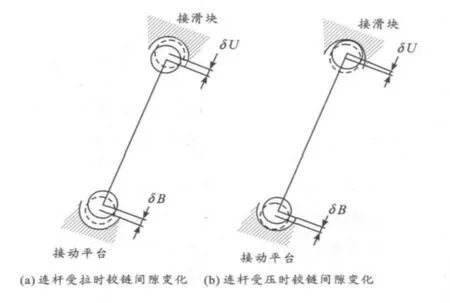
图2 铰链间隙误差

由于连杆为细长杆(静态分析时可忽略连杆质量)，由6－PSS并联机构的结构特点知，当连杆不受外载荷且机构处于静止状态时，各连杆两端所受的约束力为沿连杆方向的大小相等方向相反的拉力或压力。如图2所示，将铰链间隙误差等效成在杆长方向上产生的误差 δj，则 δji=δUi+δBi，其中 δUi、δBi分别是连杆上下铰链处的间隙值。

故有:当连杆受力为拉力时，杆长误差增加δji;当连杆受力为压力时，杆长误差减小δji。

1.3 连杆受拉受压分析

由于机构静止状态时连杆所受约束力的方向为沿连杆方向，若机构在某位姿下连杆的方向向量为ni(ni=Bi－Ai，可通过机构逆解方程求得)，则可得动平台的牛顿欧拉方程为

其中:Fli为拉杆对动平台的力;Gp为动平台重力，ri为下铰链到平台中心的矢量;Fp和Mp分别为动平台受的外力及外力矩。

显然 Fi为正时杆长误差为 δli－δji，Fi为负时杆长误差为 δli+ δji。

2 误差标定模型

综合考虑机构所有误差参数，由机构特点可知:滑块初始位置误差和上铰链位置误差以及杆长误差和铰链间隙误差很难解耦。将滑块初始位置误差并入上铰链位置误差来考虑，不影响机构的标定精度。

由于当连杆受力为拉力时，杆长误差记为δli+δji;当连杆受力为压力时，杆长误差记为δliδji。故可以分别标定 δli+ δji和 δli－ δji，即可做到杆长误差δli和铰链间隙误差δji的分离。

由机构运动学方程可以得到机构的误差标定方程为

其中:[δAixδAiyδAiz]为上铰链位置误差;[δB'ixδB'iyδB'iz]为下铰链在动平台坐标系下的位置误差(［δBixδBiyδBiz］T=R［δB'ixδB'iyδB'iz］T);［δaixδaiyδaiz］为导轨的直线度误差。

由式(4)可知:方程含有杆长误差(将δli±δji看作一项)、上下铰链位置误差、以及导轨直线度误差共10个未知量，6个支链共有60个未知量，而测得的每个位姿可列6个方程，这样需要测量至少10个合适的位姿解;又由上下铰链位置误差的关系知，10个位姿解中至少要有4个姿态不同的解才能对其解耦。

当测得足够多的位姿数据时，可以应用最小二乘法求解各误差量，假如测得N组动平台末端位姿数据，以及与末端位姿相对应的滑块输入参数值，可以建立目标函数:

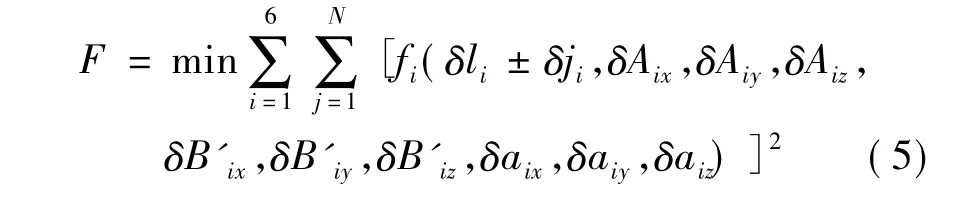
令 W= ［δli± δji，δAix，δAiy，δAiz，δB'ix，δB'iy，δB'iz，δaix，δaiy，δaiz］，则误差方程(5)可写为

由于误差方程为非线性方程组，而求解非线性方程的最小二乘解相当困难，需要采用线性化方法获得线性方程。对式(6)进行泰勒级数展开，省略高阶余项，令 W0=0为变量的近似向量，则有:

对式(7)进行迭代计算，当求解的误差参数值使目标函数足够小时，停止迭代，求得误差参数值。分别解得 δli+ δji和 δli－ δji，即可将杆长误差和铰链间隙误差分离开，从而获得较精确的结构参数误差值。

图3 姿态( －20°，50°，－30°)连杆受力情况

3 应用实例

6－PSS并联机构参数:导轨间跨距为400 mm和500 mm;连杆1、3、4、6 取1600 mm，连杆2、5 取1440 mm;动平台为一个530 mm×400 mm的矩形板加一个向上倾斜30°的280 mm×240 mm翘板组成的平台。

根据机构运动空间要求，在适当范围内选取几组特殊的动平台末端姿态，用Matlab软件计算动平台姿态角不变时在各空间位置下各连杆的受力情况。

由图3可知连杆受力情况:当动平台姿态为( －20°，50°，－30°)时，各连杆受力一直为拉力;同理，进一步找出3个或更多连杆都受拉力的位姿，可以计算得到，动平台姿态角为(0°，20°，0°)时各连杆一直受拉力，姿态角为(20°，50°，30°)时在－800 mm≤z≤－1000 mm区域内连杆全都受拉力，动平台姿态为(－20°，50°，30°) 且－1100 mm≤z≤－1300 mm时连杆全都受拉力。

选用激光追踪仪进行末端位姿的测量，在机构静止状态下，在以上4个位姿区间内测得10组动平台末端位姿参数，并记录每个位姿相对应的一组滑块输入控制值(如表1所示)，可以求得一组误差值:δli+ δji、δAix、δAiy、δAiz、δBix、δBiy、δBiz、δaix、δaiy、δaiz，i=1，2，…，6。

为将 δli和 δji解耦，还需解出1组数值 δliδji，再选取另外2组动平台位姿，机构姿态为( －20°，10°，30°)且 z≤ －1100 mm 的区域内拉杆2、3、4、5 一直受压力，位姿为( －20°，10°，30°)且z≥－1100 mm的区域内杆件1、6一直受压力。表2为测得2组位姿值，由这2组位姿数据可以解出 1 组 δli－ δji，从而求得 δli和 δji，最终可得所有误差项标定值，如表3所示。

表1 拉杆受拉时机构位姿测量值 mm

表2 拉杆受压时机构位姿测量值mm

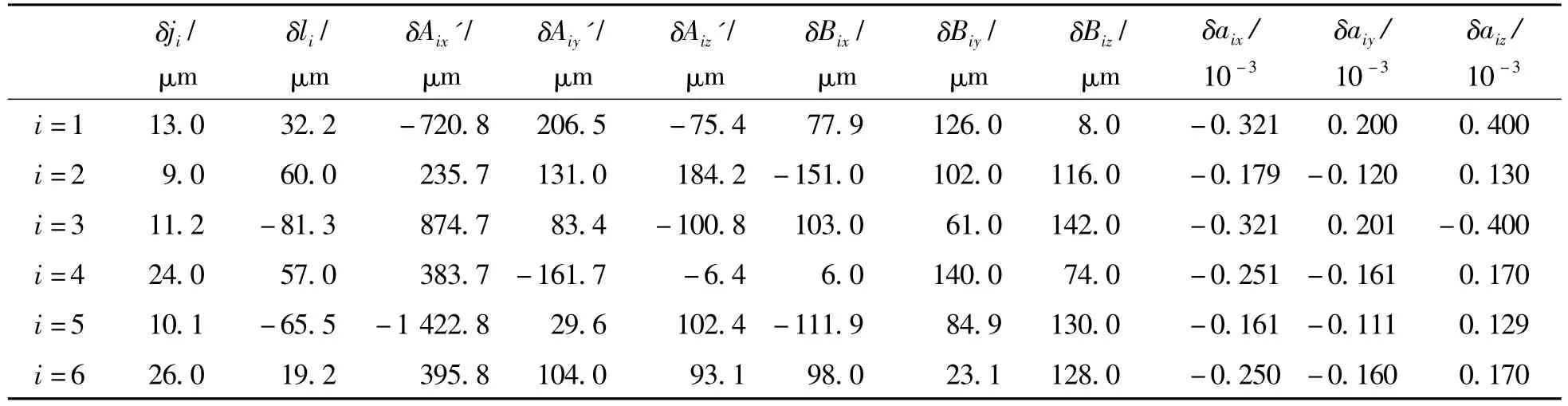
表3 标定的误差参数值

4 结束语

本文对并联机构的标定，引进了导轨直线度误差及铰链间隙误差，对机构误差项的考虑更全面，并将杆长误差和铰链间隙误差有效地分离开来，对杆长误差的标定更准确。此标定法简单有效，为此类机构的误差标定提供了依据。

［1］Jeha Ryu，Jongeun Cha.Volumetric error analysis and architecture optimization for accuracy of HexaSlide type parallel manipulators［J］.Mechanism and Machine Theory，2003，38:227 －240.

［2］Yao Rui，Li Tiemin.Error Analysis and Distribution of 6－SPS and 6－PSS Reconfigurable Parallel Manipulators［J］.Tsinghua Science and Technology，2010，15(5):547－554.

［3］Mansour Abtahi，Hodjat Pendar.Experimental kinematic calibration of parallel manipulators using a relative position error measurement system［J］.Robotics and Computer-Integrated Manufacturing，201026:799 －804.

［4］张娟，高锋阳，蒋兆远.基于激光干涉仪的数控机床几何误差辨识与补偿［J］.兰州交通大学学报，2009，28(6):46－49.

［5］王金栋，郭俊杰.基于激光跟踪仪的数控机床几何误差辨识方法［J］.机械工程学报，2011，47(14):13－19.

［6］任永杰，邾继贵.利用激光跟踪仪对机器人进行标定的方法［J］.机械工程学报，2007 ，43(9):195－200.

［7］裴葆青，陈五一，王田苗.6UPS并联机构铰链间隙误差的标定与精度分析［J］.机械设计与研究，2006，22(4):35－38.

［8］李成刚，尤晶晶，吴洪涛.并联式六维加速度传感器动力学模型研究［J］.压电与声光，2011(6):898－900.

［9］陈莉，张宏立.粒子群算法在六自由度并联机器人位置正解中的应用［J］.重庆理工大学学报:自然科学版，2010(8):86－90.

［10］李娟，孙立宁，刘延杰.一种新型平面并联定位机构的误差建模与分析［J］.压电与声光，2009(2):284－289.