应用反演谱分解去除调谐效应的分频AVO技术
2012-09-18宁媛丽韩立国周子阳倪冬梅吕寅寅
宁媛丽,韩立国,周子阳,倪冬梅,吕寅寅
(1.吉林大学 地球探测科学与技术学院,吉林长春 130026;2.核工业航测遥感中心,河北石家庄 050002)
应用反演谱分解去除调谐效应的分频AVO技术
宁媛丽1,韩立国1,周子阳2,倪冬梅1,吕寅寅1
(1.吉林大学 地球探测科学与技术学院,吉林长春 130026;2.核工业航测遥感中心,河北石家庄 050002)
传统的AVO分析是假设平面波入射到分开两个半空间的单界面,并没有考虑油藏厚度的影响。当地层为薄层时,调谐效应会使AVO的变化规律发生改变,影响储层的识别。谱分解能够将时间记录转换到不同频率,从而得到更多的储层信息。因此,可以利用谱分解进行分频AVO分析。在多种谱分解方法中,反演谱分解方法具有较高的时频分辨率,并且其直接得到的是反射系数谱,可去除子波的影响。依据这一特性,这里将反演谱分解方法用于去除调谐效应。根据实际薄层的物理参数和地质条件,设计不同厚度的薄层模型,正演得到合成地震道集;然后利用反演谱分解进行分频AVO分析。结果表明,该方法能够消除薄层调谐效应,同时还能避免陷频现象。
薄层;调谐效应;陷频;反演谱分解;分频AVO
0 前言
AVO技术研究地震反射振幅随偏移距(或入射角)的变化规律,已成为当今油气储层预测一项常规的技术。当前AVO技术研究的主要是单界面或厚层,没有考虑地层厚度变化的影响,而薄层很可能就是储层单元。因此,随着勘探精度要求的提高,进行薄储层AVO分析对隐蔽性油气藏的开发具有重要意义。
Widess[1]讨论了岩层厚度对反射特征的影响,指出1/4波长时干涉最大,称之为调谐厚度,1/8波长是分辨率的极限。事实上,当地层厚度小于1/4波长时就很难分辨出来,我们将小于这个厚度的地层称为薄层。前人关于薄层的研究主要是针对确定薄层厚度展开的[2~6],而且其中很多是通过谱分解实现的[3~5]。
由于薄层有可能是储层的重要流体单元,在确定其厚度的同时,还需要研究它的AVO响应。而在薄储层中,受调谐效应影响,很难提取出有关储层的有用信息。因此,为了更好地分析薄储层除厚度以外的一些其它属性信息,必须要校正薄层调谐效应的影响[7、8]。赵伟等[9]和陈小宏[10]分析了薄互层调谐效应对AVO的影响。Wiley[11]通过对经过短时傅里叶变换的谱分解数据进行反褶积,来消除调谐效应的影响。
谱分解能将时间域信号转换到不同频率进行分析,进而得到更多的地层信息。Chapman等人[12~14]研究了分频AVO分析,得到不同频率包含的储层属性,进一步加强了地震解释的精确度Portniaguine等人[15~17]研究了反演谱分解算法并应用于确定薄储层厚度和提高地震分辨率Charies I.Puryear等人[18]详细说明了利用谱反演确定薄层厚度和进行地层解释的理论和应用。反演谱分解得到的结果是一个稀疏反射系数反演结果,在反演过程中去除了子波的影响,因此可以用来消除薄层的调谐效应。作者在本文首先建立了不同厚度薄储层模型,分析其AVO特征,指出薄层调谐效应的影响。然后用L1范数做约束的基追踪优化算法反演谱分解进行分频AVO分析。最终目的是消除或降低薄层调谐效应对AVO分析的影响,文中合成记录例子给出了结果。
1 基本原理
1.1 薄层调谐效应
薄层是以它的纵向分辨率为依据的,对地震子波来说,不能分辨出顶、底反射的地层即为薄层。由于地震子波的频率、延续长度和波长是可以改变的,所以薄层的厚度是相对的。
当薄层上界面反射子波与其底界面的反射波同时到达地面检波器时,将引起波的干涉(如图1所示),波的干涉所形成的合成波的振幅是增强还是减弱,取决于地震波之间的相位关系。反射双曲线远道时差减小引起的相邻两反射子波相互干涉,也会影响振幅特性。陆相沉积含气砂岩上下往往是一套砂泥岩薄层序列,波的干涉是影响目的层砂岩反射振幅的一个重要因素。因此,在AVO研究中,要考虑波的干涉和由于干涉引起的薄层调谐产生的影响。
1.2 陷频现象
薄层相当于一个滤波器,改变了入射波的频谱特性。薄层的振幅谱是一个周期谱,如图1所示,陷频周期性的出现。Partyka等人[3]和Partyka[16]指出,在关于频率的振幅谱中楔形模型的时间厚度决定陷频周期,即陷频周期是时间厚度的倒数:

式中 Pf是振幅谱中的陷频周期,单位为Hz;t为薄层的时间厚度,单位为s。
也可以认为在关于时间厚度的振幅谱中,频率决定陷频周期,即Pt=1/f。虽然这个值可以用来确定薄层厚度,但陷频却使频谱形状发生了变化而谱形状的改变又会影响对岩性和渗透率等的解释。下页图2(a)是模拟的两个主频30Hz、相隔30ms的同相轴干涉形成的信号。下页图2(b)和下页图2(c)分别是合成信号经过短时傅里叶变换和反演谱分解后得到的时频谱。由于两子波相隔30ms,所以短时傅里叶变换得到的时频谱会在33 3Hz、66.6Hz等频率出现陷频,这与我们选取的子波主频30Hz比较接近。从图2中可以看出,陷频引起了子波频谱的畸变,而反演谱分解得到的时频谱(见下页图2(c))避免了这种现象的发生。
1.3反演谱分解
地震褶积模型是指一个地震信号s,是由一个子波w褶积上地下反射系数序列r得到,即w*r=s。将褶积式用一个线性系统表示,即一个矩阵与一个向量相乘,得到一个向量的形式,即Wr=s其中W为子波w的褶积矩阵,它具有Toeplitz矩阵的形式。
地震褶积模型得到的地震记录与输入子波的频率是一致的,而实际地震记录中含有不同的频率成份,所以通过许多不同频率的子波和对应频率的伪反射系数(区别于真实的地下反射系数),地震信号s可以由式(2)叠加而成。

式中 wi为单一频率为fi的子波,i=1、2、…Nf;ri为其相应的伪反射系数序列。
将式(2)化为矩阵与向量相乘的线性系统形式,可以表示为式(3)。
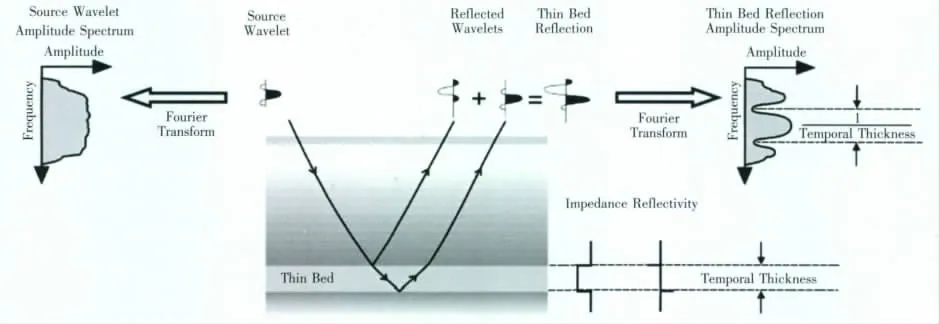
图1 薄层反射及其频谱[3]Fig.1Thin-bed spectral imaging[3]
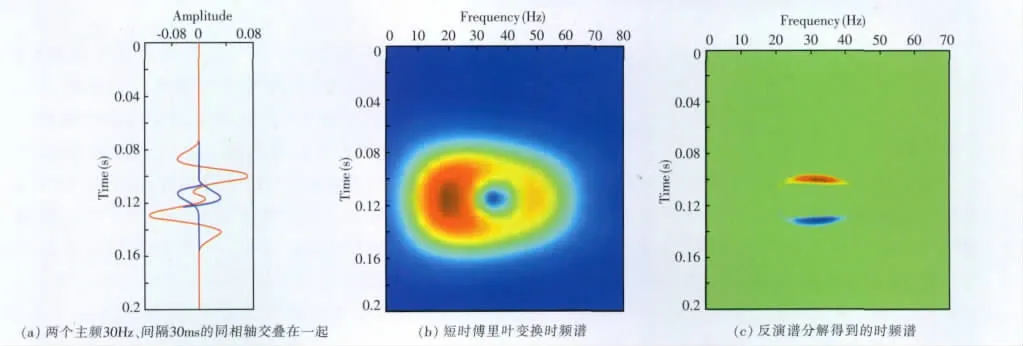
图2 薄层陷频Fig.2 Notch of thin bed
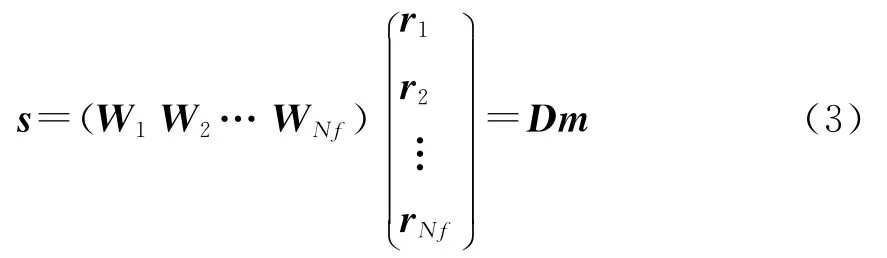
其中 Wi频率为子波wi对应的褶积矩阵;D就代表子波褶积矩阵库;m为伪反射系数序列矢量。
这样给定子波褶积矩阵库D,就可以通过解反问题从地震记录s中分解出伪反射系数序列矢量m。将m化为(r0r1…rNf)的形式,这个数据是以时间和频率为纵横坐标的矩阵形式,即为反演时频谱。因为信号s的维数为Nt+Nf-1,而要求的伪反射系数序列m的维数为Nt×Nf,因此从Dm=s中解m是一个欠定反演问题。
欠定线性系统是通过将模型或数据残差的某种观测值最小化解决的,在地球物理反演中,常使用L2范数作为误差测量。L2范数的优点是效率高,可以通过QR分解等实现;缺点是L2范数只对高斯背景适用,对含大异常数据太敏感。谱分解反演问题要求稀疏解,L1范数在求稀疏解方面比L2范数效果要好。L1范数对误差大的数据不敏感,但对零误差数据(或模型参数)有无穷大的权重。因此从效果和计算量考虑,互相约束的L1和L2范数条件会更好。
基追踪(Basis Pursuit)方法是对欠定系统求稀疏解的一个好方法,正好适合谱分解反演问题。我们在本文中采用L2范数约束的L1范数基追踪解,如式(4)。
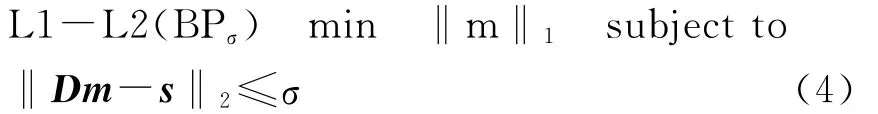
由上述基本理论可知,反演过程消除了子波影响,得到稀疏反射系数。那么,反演谱分解后再进行AVO分析,就可以减小薄层调谐效应对AVO分析的影响。将反演谱分解与连续小波变换(CWT)方法进行比较(见下页图3)。分别用两个极性相反的30Hz雷克子波间隔80ms、30ms、10 ms、5ms合成信号,组成一道地震记录,如图3(a所示。然后对合成记录分别做反演谱分解和CWT,得到时频谱见下页的图3(b)和图3(c)。比较这两种谱分解方法得到的结果。可以看出,反演谱分解比CWT有更好的时间分辨率和频率分辨率。当两个子波间隔在10ms及以下时,CWT已经不能将其分辨出来,而反演谱分解可清晰地分辨出来,同时还能够显示出极性。当两个子波间隔30ms时,CWT方法得到的时频谱可以看到明显的陷频现象,而反演方法却没有。
2 分频AVO
AVO技术是估算地下弹性特征差异的有效工具,它的理论基础是Zoepprite方程。传统AVO分析的前提是假设平面波入射到分开两个半空间的单界面,并没考虑油藏厚度等因素对分析的影响。而地震反射振幅随偏移距的变化,会受到地层厚度等因素的影响。实际上地下一个薄层介质的AVO响应与厚层介质的特性是不一样的,如果不考虑这些因素,将会造成烃类储层预测的错误。因此,一些地球物理学家尝试进行分频AVO分析LI等人[8]指出,当薄层的模型一定时,调谐效应会使不同频率子波AVO曲线发生变化。分频AVO技术考虑了频率因素,在不同频率下进行AVO分析,这样可以进一步提高地震勘探的精度。利用地震谱分解技术不仅可以有效识别储层时间厚度的变化,还可以进行薄互层气藏的AVO研究。
3 数值模拟
3.1 模型
为了分析薄层调谐对AVO分析的影响,我们基于Zoepprite方程正演得到地震角道集,然后对薄层顶界面进行AVO分析。表1给出了地质模型参数,储层参数属于第一类AVO。我们设计了四种层厚的模型,厚度分别为76m、19m、9m、5m。模型第三层参数与第一层相同,并选用主频为35Hz的雷克子波进行正演。根据v=λf(f为子波主频)可知,一个波长厚度约为76m。图4(见下页)为各个厚度模型正演得到的地震角道集。
3.2 基于反演谱分解的分频AVO分析
图5(见下页)给出了不同厚度条件下砂泥岩界面的AVO曲线。由图5可以看出,薄层的调谐效应影响了AVO曲线形态。虽然AVO曲线的变化规律近似,但各种层厚曲线的截距和梯度却并不相同。由薄层定义可知,76m厚的储层不属于薄层,故其AVO曲线形态正常,明显可以看出属于第一类AVO;19m厚薄层的AVO曲线截距和梯度绝对值最大;其它厚度的都次之,这是因为19m厚近于四分之一波长,相长干涉使反射振幅最大;当层厚在9m以下时,薄层越薄AVO曲线形态越不明显。为了消除薄层调谐效应的影响,我们进行基于反演谱分解的分频AVO分析。经过谱分解以后,传统的地震道集转换到不同频率下。图6(见下页)为分频后选择的地震子波主频(35Hz)的频率切片。
在反演谱分解后,传统的地震道集转换到不同频率切片下,波的振幅转换为稀疏反射系数,我们可以通过这些频率切片来研究储层的一些属性,下页图6给出了不同厚度模型的35Hz频率切片经过反演谱分解后,再对储层顶界面进行AVO分析得到结果如后面的图7所示。从图7可以看到各种厚度薄层的AVO曲线与厚层曲线几乎重合这充分说明基于反演谱分解方法的分频AVO分析,可以消除薄层调谐对AVO分析的影响。

表1 模型参数Tab.1 Model parameters
4 结论
基于反演谱分解的分频AVO分析,可以消除薄层调谐效应对正常AVO分析的影响。通过比较反演谱分解和连续小波变换,可以发现反演谱分解方法具有很高的时间分辨率和频率分辨率,能够更好地识别薄层,同时还能够避免陷频引起的谱畸变。由于反演谱分解后得到的是稀疏反射系数,去除了子波的影响,因此应用其进行分频AVO分析,可成功地消除薄层调谐效应。

图3 反演谱分解与连续小波变换(CWT)比较Fig.3 Comparison of spectral inversion and continuous wavelet transform

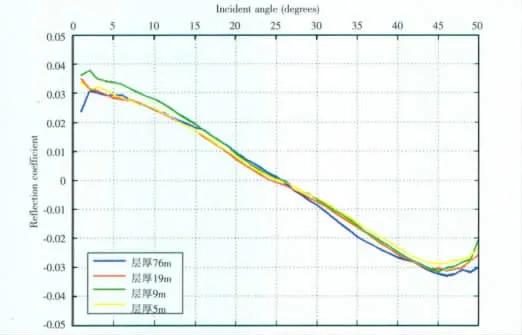
图7 不同厚度储层分频AVO响应比较Fig.7 Comparison of frequency-dependent AVO response of reservoir with different thickness
由于作者在正演模拟采用了Ricker子波,所以子波矩阵应由不同频率的Ricker子波建立。而对于实际数据,首先需要提取子波,再将提取的子波转化到不同频率建立子波库,也可根据记录中子波的相位选择Ricker子波(零相位)、最小相位子波等现成子波反演。
致谢
感谢韩利在反演谱分解方面的帮助。
[1] WIDESS M B.How thin is a thin bed[J].Geophysics,1973,38(6):1176.
[2]BROWN A.Interpretation of three-dimensional seismic data.AAPG[M].1991.
[3] PARTYKA G,GRIDLEY J,LOPEZ J.Interpretational applications of spectral decomposition in reservoir characterization[J].The Leading Edge,1999(18):353.
[4] MARFURT K J,KIRLIN R L.Narrow-band spectral analysis and thin-bed tuning[J].Geophysics,2001(66):1274.
[5] 高静怀,陈文超,李幼铭,等.广义S变换与薄互层地震响应分析[J].地球物理学报,2003,46(4):526.
[6] ZHANG X,ZHENG X D.Thin bed identification based on attribute difference between far and near offset within prestack data:A model study[C].SEG Expanded Abstracts,2007(26):293.
[7] BAKKE N E,URSIN B.Thin-bed AVO effects[J].Geophysical Prospecting,1998(46):571.
[8] LI F,CAO S,HAN D,et al.Phase scanning method for detuning in thin bed[C].SEG Technical Program Expanded Abstracts,2009(28):346.
[9] 赵伟,陈小宏,李景叶.薄互层调谐对AVO的影响[J].石油物探,2006,45(6):570.
[10]陈小宏,田立新,黄饶.地震分频AVO发展现状及展望[J].海相油气地质,2009,14(4):60.
[11]WILEY R W,WILSON P H,PETERS S W.Removing the Thin Bed Effects from Spectral Decomposition[C].69th EAGE Conference &Exhibition London,2007.
[12]CHAPMAN M,LIU E,LI X Y.The influence o abnormally high reservoir attenuation on the AVO signature[J].The Leading Edge,2005(24):1120.
[13]LIU E,CHAPMAN M,LOIZOU N,et al.Applications of spectral decomposition for AVO analyses in the west of Shetland[C].SEG Technical Program Expanded Abstracts,2006(25):279.
[14]ODEBEAT E,ZHANG J,CHAPMAN M,et al Application of spectral decomposition to detection o dispersion anomalies associated with gas saturation[J].The Leading Edge,2006(25):206.
[15]PORTNIAGUINE O,CASTAGNA J.Inverse spectral decomposition[C].SEG Technical Program Expanded Abstracts,2004(23):1786.
[16]PARTYKA G.Spectral decomposition[C].SEG Spring 2005Distinguished Lecture,2005.
[17]PURYEAR C I,CASTAGNA J P.An algorithm fo calculation of bed thickness and reflection coefficient from amplitude spectrum[C]..SEG Technical Program Expanded Abstracts,2006(25):1767.
[18]PURYEAR C I,CASTAGNA J P.Layer-thicknes determination and atratigraphic intertation using spectral inversion:Theory and application[J].Geophysics,2008,73(2):R37.
[19]崔凤林,管叶君.时频分析—薄互层结构研究的新途径[J].石油物探,1992,31(2):1.
[20]SIMMONS J L,BACKUS M M.AVO modeling and the locally converted shear wave[J].Geophysics 1994,59(3):1237.
[21]MARMALYEVSKYY N,ROGANOV Y.Frequency depending AVO for a gas-saturated periodical thin-layered stack[J].The Leading Edge,2005,24(11):1120.
[22]FRED J,HILTERMAN.地震振幅解释[M].孙夕平,赵良武,张研,等,译.北京:石油工业出版社2006.
[23]刘亚茹.薄互层正演模拟及特征分析[D].北京:中国石油大学,2007.
[24]陈守田,孟宪禄.薄互层储层预测方法[J].石油物探,2004,43(1):33.
book=81,ebook=81
1001—1749(2012)03—0243—06
P 631.4
A
10.3969/j.issn.1001-1749.2012.03.01
宁媛丽(1985-),女,硕士,研究方向为分频AVO。
国家“973”项目(2007CB209603);国家“863”项目(2007AA060801)
2011-07-19改回日期:2012-02-21
