基于非线性函数的非平稳盲源分离步长算法

李著成

（北京联合大学商务学院，北京 100025）

自然梯度算法是盲源分离的一种经典算法，但由于其固定步长的应用，造成了两个重要的算法性能指标收敛速度和稳态误差之间的矛盾。一般来说，大的步长收敛速度较快，但稳态误差较大;反之，小的步长收敛速度较慢，但稳态误差较小。特别在分离非平稳盲源时，这种矛盾会尤为明显［1－2］。

1 系统模型和算法公式

假设有n个相互统计独立的未知源信号s（t）=［s1（t），s2（t），…，sn（t）］T，t为离散时间，经过未知的传输信道A∈ Rm×n后得到m个观测信号x（t）=［x1（t），x2（t），…，xm（t）］T（通常情况下m≥n），写成矩阵形式为

盲源分离的任务是只根据观测信号x（t），通过某种学习算法得到的分离矩阵W∈Rn×m，使得

其中各分量之间尽可能地独立，依此将y（t）=［y1（t），y2（t），…，yn（t）］T作为对源信号的一个估计，若

式中:G为全局矩阵;I为n×n维单位矩阵。则y（t）=s（t），那么源信号得到彻底恢复［3］。

盲源分离的系统模型如图1所示。

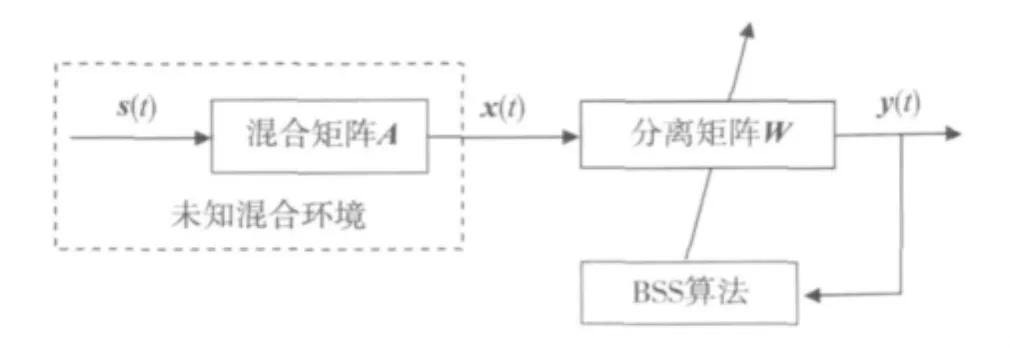
图1 盲源分离的系统模型

基于互信息（Mutual Information，MI）的自然梯度盲源分离算法［4］最早由 Amari，Cichoki等人提出，代价函数为

由表4主成分综合得分可知，各土壤样本养分含量由高到低的排列顺序为17→28→18→25→23→15→40→24→27→11→33→7→32→1→5→26→3→9→12→10→14→48→2→29→16→31→41→34→38→37→44→4→45→47→21→46→36→20→30→6→13→19→8→43→22→39→35→49→42。

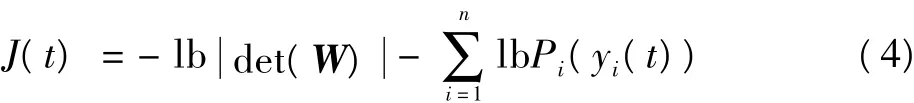
式中:Pi（yi（t））为yi（t）的概率密度函数;det（·）表示矩阵的行列式。按照式（5）更新分离矩阵

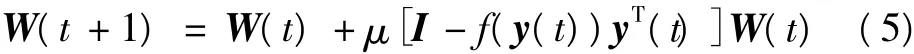
式中:μ为步长因子;f（y（t））=［f1（y1（t）），f2（y2（t）），…，fn（yn（t））］T为估计信号y（t）的非线性函数，理想情况下有

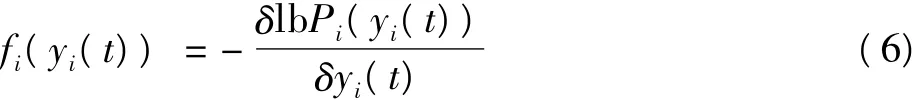
式（4）对处理类似声音、语言、生物医学和机械振动等非平稳信号不是很理想，对其进行如下的修改［4－6］:

W（t+1）=W（t）+μ［Λ －f（y（t））yT（t）］W（t）（7）式中:Λ是一个对角阵，其元素为矩阵f（y（t））y（t）T对角线上的元素，即 Λ =diag［f（y（t））yT（t）］（diag［·］表示由矩阵对角线元素构成的对角阵）。

2 基于非线性函数的步长算法

为了克服收敛速度和稳态误差之间的矛盾，考虑采用变步长的办法，使步长随着算法分离的实际情况做动态的变化，本文提出一种基于非线性函数的步长算法，通过某种误差的相关值e（t）e（t－1）去调节步长，表达式为

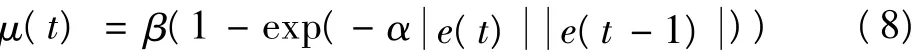
式中:e（t）是稳态误差;β＞0和α＞0为算法参数，这两个值的选择对算法性能会产生一定影响。

对于非平稳源信号，算法收敛后分离信号y应该满足［4］

式中:E［·］为数学期望。这意味着为了满足式（9），分离信号的幅度在算法执行过程中会不断自动调整。

假设

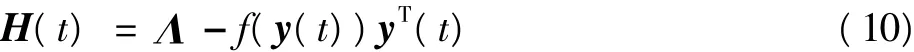
它的分量形式应满足

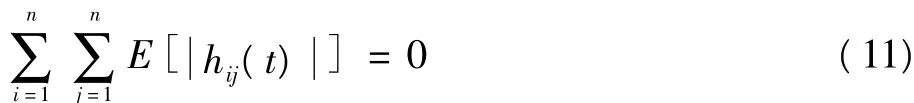
由此可以得到误差的一种表达式为

结合式（8）和式（12），新的变步长算法为

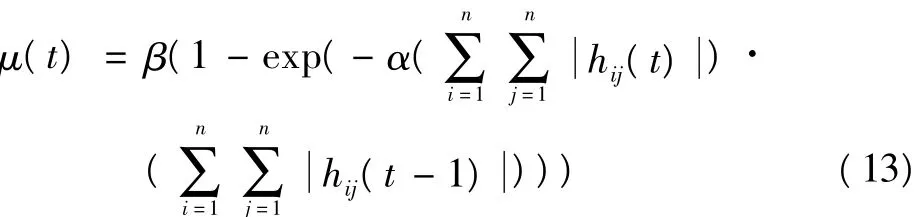
值得注意的是，μ（t）如果选择的太大，对算法的稳定性会造成较大的影响。因此，必须考虑步长μ（t）的上界

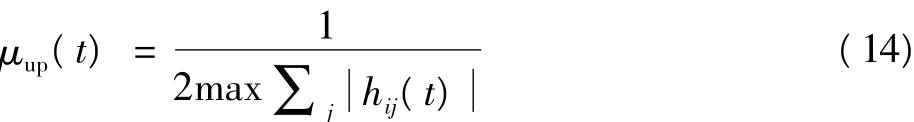
式中:μup（t）为μ（t）的上界。此时，μ（t）的取值为

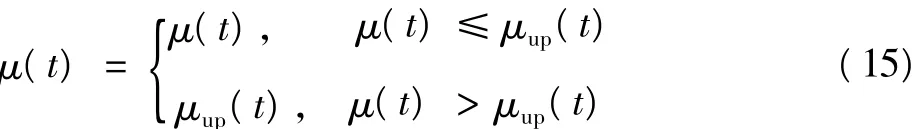
如果步长不超过μup（t），则按照式（13）的步长，如果超过了μup（t），步长应选取为μ=μup（t）。

3 MATLAB仿真实验

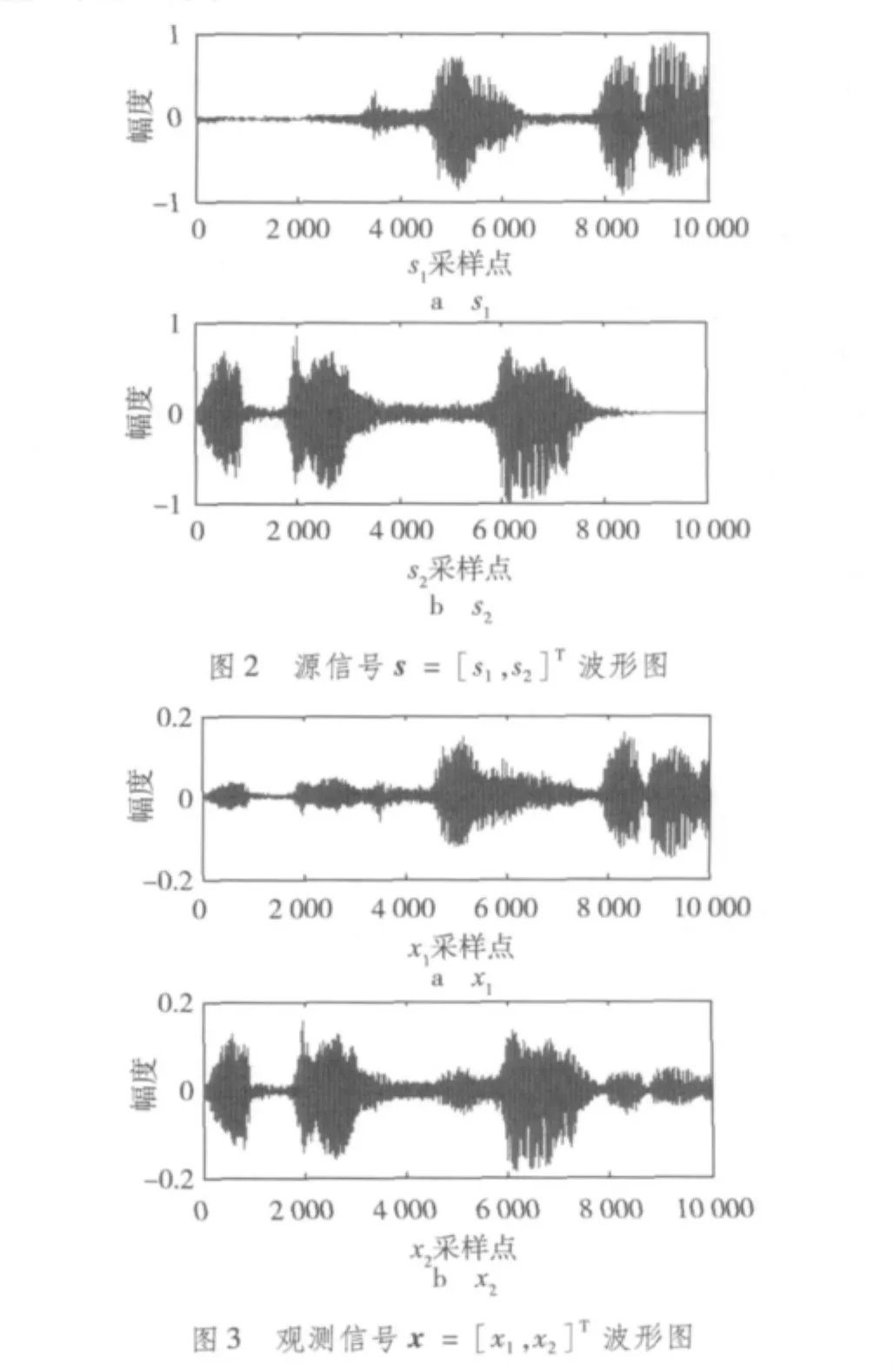
假设n=m=2，未知非平稳源信号s（t）=［s1（t），s2（t）］T为用Soundblaster卡采集的2路语音信号，其波形如图2所示，μ =0.006，β =0.05，α =3。图3为源信号经过随机混合矩阵A混合后生成的观测信号x（t）=［x1（t），x2（t）］T的波形图。图3与图2相比较，波形图发生了明显的改变。

为验证提出算法的有效性，分别用新旧两种算法对上述观察信号进行分离，分离效果通过盲源分离技术常用的一种算法评价指标——串音误差Cte（Cross－talk error）来鉴定，其表达式为

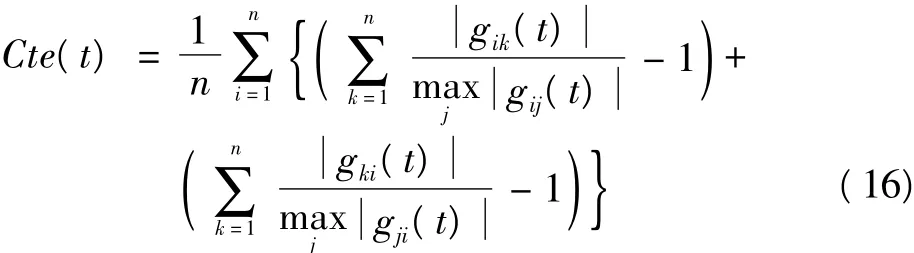
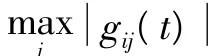
图4为经过新算法分离出的源信号的估计信号y（t）=［y1（t），y2（t）］T的波形图。将图4与图2进行比较，可直观地看出新算法已基本完成对源信号的恢复，y1对应于s1，幅度和相位发生了改变;y2对应于s2，相位没变但幅度发生了改变，这些改变是由盲源分离的不确定性决定的，在实际应用中，只要保持波形不变，这是完全可以接受的。图5是基于非线性函数的步长算法与固定步长算法的Cte比较图，表1为两种算法的更新次数与Cte的对应值。结合图5和表1可知，新算法与旧算法相比，分离效果有了明显改善，收敛速度较快而稳态误差较小，固定步长算法分离出源信号需更新200次左右，而新的自适应算法只需135次，收敛速度明显加快，而且此时新的步长算法的Cte=0.04，固定步长算法的Cte=0.08，可见稳态误差也有一定程度的改善。

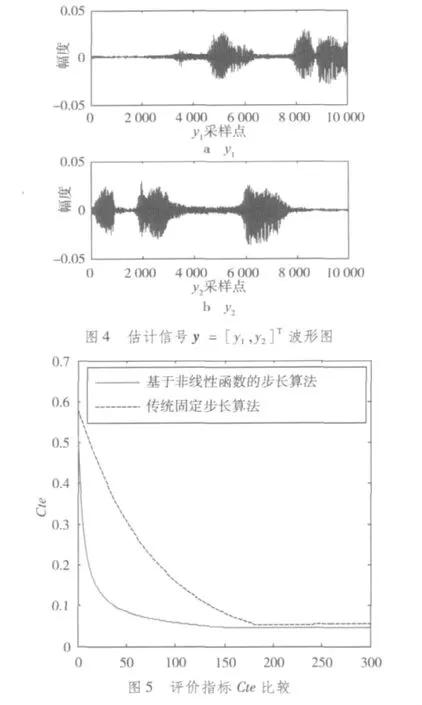
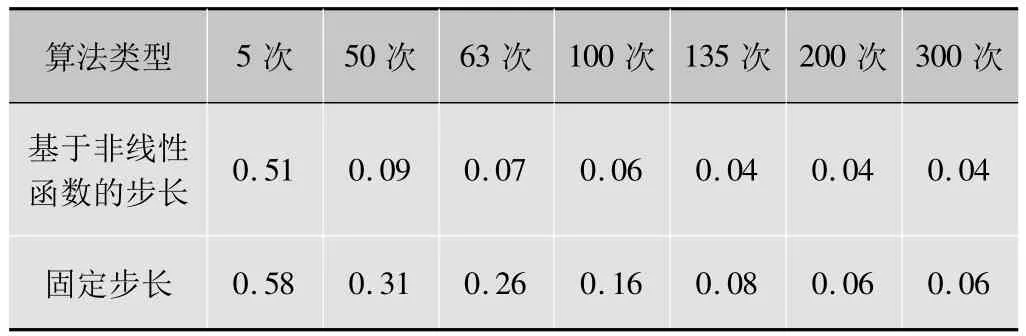
表1 两种算法的更新次数与Cte的对应值

关于式（13）中α和β值的选择，经过实验也发现了一定的规律。一般地，0＜α＜1，β＞1，如果要求收敛速度快，就应选择一个较大的β值，如果要求稳态误差小，就应选择一个较小的α值，β影响全局而α影响局部。

4 小结

收敛速度和稳态误差一直是盲源分离算法研究的热点之一。本文在对自然梯度算法进行分析的基础上，提出了一种新的基于非线性函数的步长算法，在加快算法收敛速度的同时兼顾减小稳态误差，克服了传统固定步长算法的缺点，通过计算机仿真实验证明了该算法的有效性。

：

［1］NAKAJIMA H，NAKADAI K，HASEGAWA Y，et al.Adaptive step－size parameter control for real－world blind source separation［C］//Proc.IEEE International Conference on Acoustics，Speech and Signal Processing，2008.Las Vegas:IEEE Press，2008:149－152.

［2］OU Shifeng，GAO Ying，JIN Gang，et al.Variable step－size algorithm for blind source separation using a combination of two adaptive separation system［C］//Proc.15th International Conference on Natural Computation，2009.Tianjin，China:IEEE Press，2009:649－652.

［3］桑睿，吴杰.一种解决频域盲源分离模糊度问题的新方法［J］.电视技术，2011，35（15）:122－155.

［4］CICHOCKI A，AMARI S.Adaptive blind signal and image processing:learning algorithm and applications［M］.New York:Wiley，2002.

［5］AMARI S，CICHOCKI A.Adaptive blind separation processing－neural network approaches［J］.Proceedings of the IEEE，1998，86（10）:2026－2048.

［6］ZHANG Kun，CHAN Laiwan.Convolutive blind source separation by efficient blind deconvolution and minimal filter distortion［J］.Neurocomputing，2010，73（13/14/15）:2580－2588.