子宫肌瘤MRI影像非刚性配准研究

所世腾，张良宾，李跃华，陈亚珠，张 素

0 引言

子宫肌瘤是女性生殖器最常见的一种由子宫壁肌肉和纤维组织所构成的良性肿瘤，多见于30-50岁的妇女，是导致子宫切除的主要原因之一。临床结合超声和CT能做出较准确的诊断，但是MRI对组织分辨率高，定位、定性的正确率高，在子宫肌瘤诊断中已成为一种重要的手段。典型的子宫肌瘤MRI表现具有特征性[1]，T1加权呈等信号、T2加权呈低信号。子宫肌瘤体渲染示意图，如图1所示：

图1 子宫肌瘤体渲染示意图

作为近年来兴起的治疗肿瘤的有效方式，高强度聚焦超声(High-Intensity Focused Ultrasound, HIFU)治疗可以非侵入地将足够能量的超声波聚焦到病灶区域，让局部温度升高使组织凝固性坏死或达到药物释放条件，达到病灶治疗的目的[2][3]。HIFU和磁共振技术结合(MRI-guided HIFU,MRgHIFU)采用 MRI进行目标定位、治疗规划和能量沉积的闭环控制，保障热消融不伤及周围组织。作为MRgHIFU关键技术之一的图像配准技术是治疗计划制定与实施二者之间的联系纽带，它也是校正定位误差，实施精确治疗的基础。

本文主要针对 MRgHIFU治疗子宫肌瘤所采用的配准技术进行阐述，着重讨论基于FFD模型的非刚性配准方法并将其应用到子宫肌瘤MR影像中。

1 医学图像配准

对于在不同条件下获取的两组医学图像进行配准，就是要找到一个合适的相似性测度(similarity measure)函数，然后通过求解得到一个空间几何坐标变换关系，使得经过求得的空间变换之后，两组图像之间的相似性能够达到最大。医学图像配准主要包括空间变换、插值方法、优化算法和相似性测度四个主要过程。

2 基于FFD的非刚性配准

这里采用本实验室研究的基于B样条的FFD模型[4]。FFD模型对于三维物体形变的建模是一种有效的方法，它采用一组形变物体上的网格点来控制整个变形。

2.1 基本思想

基于FFD模型的非刚性配准主要分四步：构造网格空间，嵌入被变形物体，对网格空间进行变形，重建被变形物体。

2.2 插值方法

鉴于PV插值会给互信息函数曲线在整数网格点处带来局部极大值，局部极值点的出现有时会阻碍配准算法的全局优化进程，从而导致算法无法收敛到全局最优，影响配准的精度。这里采用的是基于PV插值算法的HPV插值[4]。

2.3 相似性测度

根据配准所依据的图像特征，相似性测度可以分为基于几何特征和基于像素灰度两类。其中基于像素灰度的相似性测度是目前应用较为广泛的一类测度，在单模态和多模态、刚性配准和非刚性配准中均适用，相对于基于几何特征的配准方法，精确性和稳定性更好。常用的相似性测度方法有最小均方误差(Mean Square Error, MSE)、相关系数(Correlation Coefficient, CC)、互信息(Mutual Information, MI)等。

一般来讲，客观实际物体的形变不是任意的，对形变场施加一定的约束条件，保证形变能够在适当的范围内进行，以便更加真实的模拟器官的形变，使得结果更加有意义，Wahba描述了平滑约束项的一般形式。为了使基于 B样条的FFD模型的形变平滑、连续，我们将平滑约束项扩展成3D，如公式（1）

为寻找最优化的空间变换参数，需要构造代价函数，通过一定的搜索策略去寻找这个代价函数的极值，对应此时取得极值的参数即为该测度下的最优变换。代价函数由两部分组成，图像的相似性测度和平滑约束项，如公式（2）

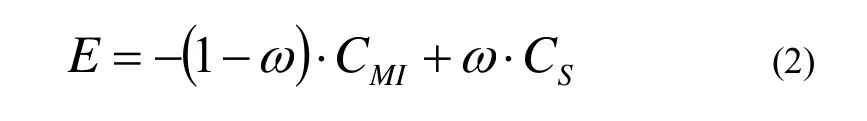
这里 ω(0≤ω<1)是权重系数，控制图像的相似性测度和平滑约束项在代价函数中所占的比例。

2.4 优化算法

医学图像配准过程一般是一个优化过程。公式(2)已经给出了非刚性配准算法的代价函数，为了寻找最佳参数Φ，需要利用优化方法来最小化代价函数E，即如公式（3）

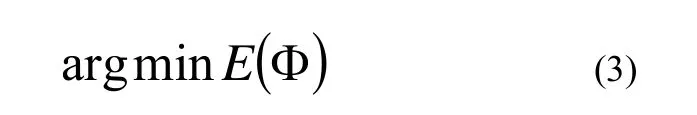
现有的优化算法有很多，由于基于B样条的FFD模型的参数空间巨大，不宜采用搜索类寻优方法。本文采用一种简单的梯度下降[5]的迭代方法。

3 实验分析及结果讨论

3.1 仿真数据实验

在仿真数据实验中，选用的是一组Siemens磁共振T2加权图像序列，由上海交通大学附属第六人民医院提供。扫描部位是一位患有子宫肌瘤女性的盆腔，图像序列大小为320×236×24(单位：像素)。为了节省配准时计算机的内存开销、加快配准速度，先将图像序列降采样为 64×64×24，降采样后的数据作为配准的浮动图像序列。同时，我们将降采样后的数据按照公式(4)进行人工形变，再加上随机噪声作为配准的参考图像，如公式（4）

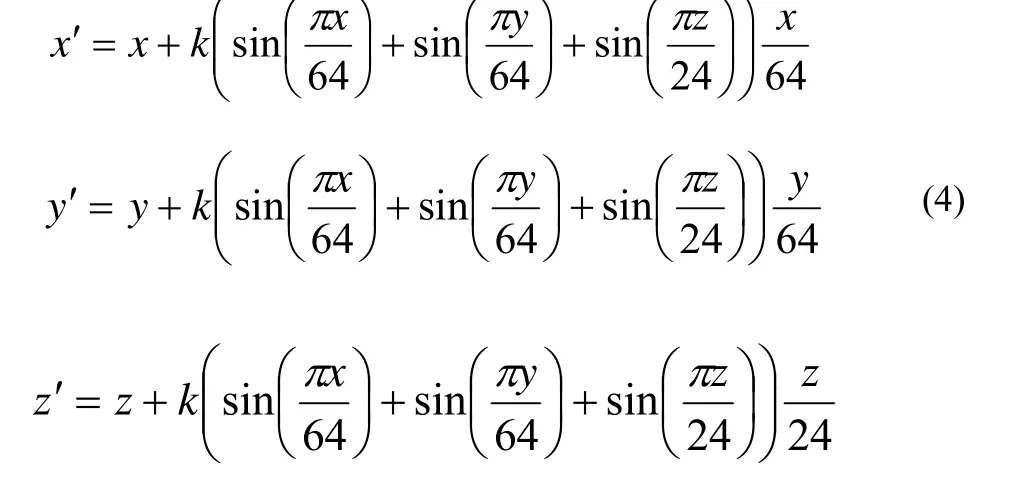
其中，x，y和z是原始图像像素点坐标，x’，y’和z’是人工形变后图像像素点坐标，k表示变形系数，数值越大，表示变形程度也越大。在浮动图像中选取一个长方体区域作为感兴趣区域(Region of Interest, ROI)，参考图像序列选取相同的ROI。非刚性配准仅在ROI上实现。

3.1.1 配准参数对结果的影响

在基于FFD模型的非刚性配准算法中，迭代次数、迭代步长和控制点的布局都会影响配准结果，参数选取的合理与否直接影响到配准的好坏。

通过实验发现参数设置的不同会对配准结果产生不同的影响。在以下实验中，我们均选取控制点布局为8×8×8，迭代步长μ=0.5。为了保证最终优化结果的收敛性，选取迭代次数为200次。

3.1.2 实验结果及与Demons算法[6]的对比

为了定量的评估基于FFD模型非刚性配准算法的性能，我们对一系列在不同k值下的仿真数据进行配准实验，并且分别计算配准前浮动图像和参考图像、配准后经配准图像和参考图像 ROI重叠区域的互相关系数(CC)、互信息(MI)和均方根(RMS)作为衡量指标判定配准结果的有效性。RMS计算公式（5）

其中，rT,qT表示两幅图像，n表示重叠区域的像素点个数。

更进一步地，我们对这一系列变形系数k值下的仿真数据用Demons算法进行配准实验，计算配准结果的互相关系数(CC)、互信息(MI)和均方根(RMS)并与FFD算法的实验结果进行比较，如表1所示：

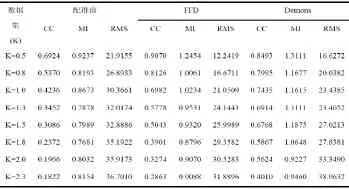
表1 子宫肌瘤仿真数据基于FFD模型非刚性配准和Demons配准结果对比

通过分析数据得知，FFD算法对于各类大小的形变都有效。对于变形较小的数据，两种算法的结果均较为精确，但是对于变形较大的数据，两种算法的精确性均有所下降，基于FFD模型的非刚性配准方法变形不是很大，可能需要较多的迭代次数才能达到要求，而Demons算法结果失真较大。

除了配准的精度，配准的速度也是评价配准算法好坏的重要指标。我们试验了三组不同的数据，分别用FFD算法和Demons算法进行配准，并记录配准过程所耗费的时间，如表2所示：

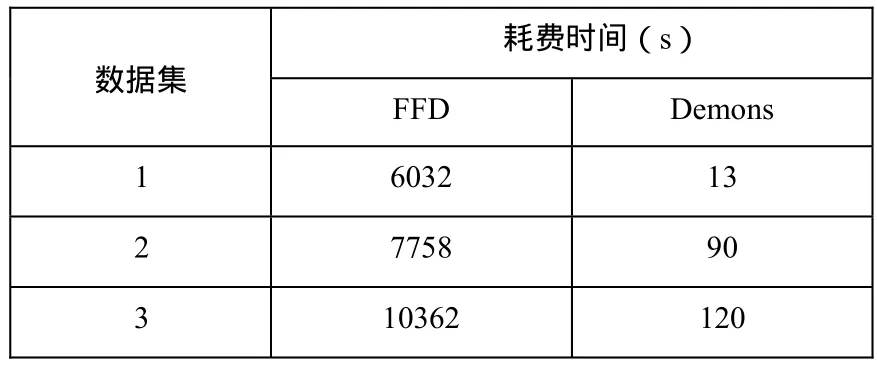
表2 FFD与Demons配准耗费时间对比

由表中数据分析可得知， FFD非刚性配准算法所花费的时间要远远超过Demons配准算法，因此，要想实时地完成配准，FFD算法还需要较大的改进。

基于FFD的非刚性配准算法在优化时采用最陡梯度下降法，需要对每一个点求梯度向量，因此控制点选取的密集程度在一定程度上影响了配准所花费的时间。在表2所列出的三组实验中，FFD耗费时间的差异主要来自于网格控制点的选取和迭代次数的不同，三个数据集的网格控制点分别选为8*8*8、8*10*10、8*10*10，迭代次数分别选为60、30、40。Demons是基于光流场模型的配准算法，配准的精度和时间依赖于图像的灰度梯度信息，因此实验中Demons算法耗费时间的差异主要在于三组数据本身形变大小的不同。

3.2 真实数据实验

在真实数据实验中，采用的数据是子宫肌瘤患者分别在两个不同时间盆腔扫描的 Philips磁共振图像，均由上海交通大学附属第六人民医院提供。T1增强扫描序列前后两组图像序列大小分别为 240×240×216(单位：像素)和224×224×240。为了方便配准，我们将所有数据前两维(,x y平面)分辨率均调整为256×256。由于真实数据的形变较大，因此实验中，首先对病例的数据进行刚性配准，目标是将ROI(如图 2(d)中红色矩形框选择的区域所示)的位置对齐，共挑选到8对特征点进行仿射变换参数的求解。配准结果参数，如表3所示：

表3 子宫肌瘤患者盆腔磁共振图像刚性配准结果参数

刚性配准结果，如图2所示：

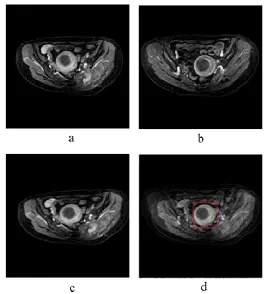
图2 子宫肌瘤患者盆腔磁共振图像刚性配准结果(显示一个层面)。其中(a)是浮动图像，(b)是通过人工挑选的相对应的参考图像，(c)是经过刚性配准后的图像，(d)是参考图像b和刚性配准后图像c的融合图像。

可以明显的看出，刚性配准结果(c)是浮动图像(a)经过旋转、平移和缩放的结果，融合图像(d)显示参考图像和刚性配准后图像比较，校正后的图像与参考图像中的空间位置是对齐的。

刚性配准是非刚性配准得以进行的前提，以刚性配准结果作为浮动图像进行基于FFD模型的非刚性配准实验，同样在待配准图像数据中选取ROI作为形变区域。

同样地，分别计算配准前后重叠区域的互相关系数(CC)、互信息(MI)和均方根(RMS)作为衡量指标比较两种算法的性能，结果如表4所示：

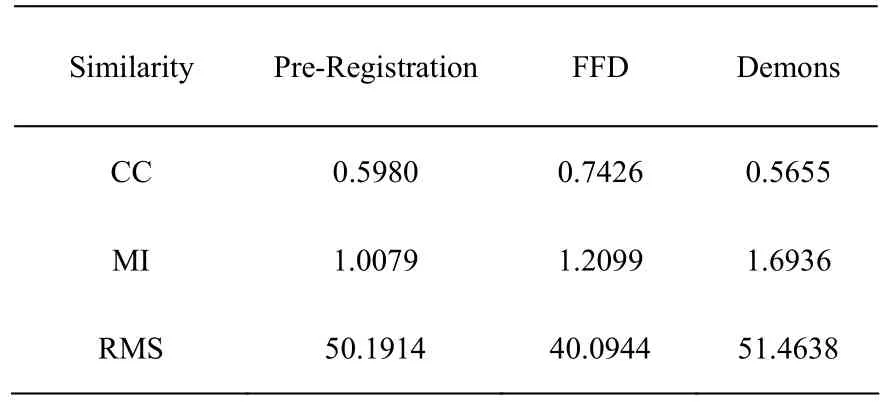
表4 子宫肌瘤真实数据基于FFD模型非刚性配准和Demons配准结果对比

可以看出，配准后，基于FFD模型的非刚性配准方法得到的结果3种相似性度量均有提高，但是Demons配准方法得到的结果CC和RMS两种指标降低，MI指标提高。图3是配准结果，从差值图来看，两种算法配准后的结果相比较配准前均有明显的提升，对比两种算法，我们发现基于FFD模型的非刚性配准算法在配准区域的整体变化跟踪有优势，Demons算法在轮廓的形变跟踪性能好。

4 总结

本文对于 MRgHIFU中的医学图像配准在子宫肌瘤治疗计划修正和跟踪方面的作用进行研究，讨论了基于 FFD模型的非刚性配准算法的应用并与Demons算法进行对比，以仿真数据实验定量测试算法的性能，以真实数据实验观察算法实际表现，为进一步将算法应用于系统中提供参考依据。

要想将FFD算法应用到临床中，配准的速度和精度需要进一步提高，硬件上可以通过采用GPU并行计算，软件上可以在相似性测度和优化策略上进行修改优化。另外，试验的真实数据量偏少，没有得到统计意义的结果，可以考虑通过更多不同成像参数的 MR数据进一步测试算法的实用性和稳定性，如图3所示：

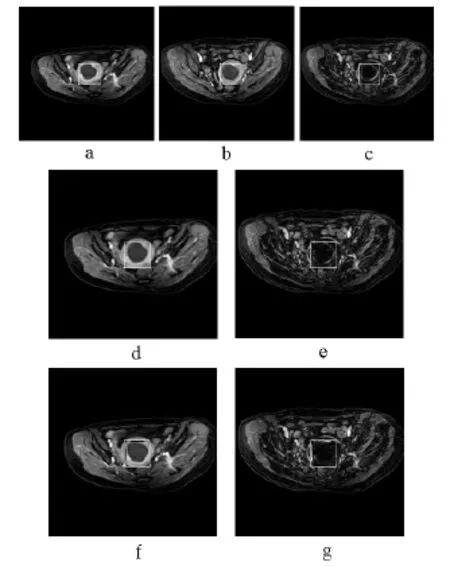
图3 子宫肌瘤患者盆腔磁共振图像序列基于FFD模型非刚性配准和Demons配准结果图(显示一个层面)。其中(a)是浮动图像， (b)是参考图像，(c)是浮动图像a和参考图像b的差值图，(d)是基于FFD模型非刚性配准后结果图，(e)是基于FFD模型非刚性配准后结果图d与参考图像b的差值图，(f)是Demons配准后结果图，(g)是Demons配准后结果图f与参考图像b的差值图。所有图像中白色矩形框表示ROI。

[1]刘欣杰, 曾燕, 赵建农, 吴伟, MRI对子宫肌瘤高强度聚焦超声治疗诊断前后的诊断价值. [J]实用放射学杂志, 2008, (5): p. 654-657.

[2]Y.F. Zhou, High intensity focused ultrasound in clinical tumor ablation. World Journal of [J]Clinical Oncology,2011.2 (1), 8-27.

[3]Fischer, K., W. Gedroyc, and F.A. Jolesz, Focused ultrasound as a local therapy for liver cancer. [J]The Cancer Journal, 2010. 16(2): p. 118.

[4]陆雪松, 聚焦超声治疗系统中的图像非刚性配准算法研究及应用. [D]上海交通大学博士学位论文, 2008.

[5]http://zh.wikipedia.org/wiki/梯度下降法.

[6]Freiman, M.Voss,S.D. Warfield, S.K. Demons registration with local affine adaptive regularization: application to registration of abdominal structures. Biomedical Imaging:From Nano to Macro, 2011 [J]IEEE International Symposium on. March 30-April 2 2011, Chicago, IL:1219-1222