基于Hough变换的海面目标检测仿真平台
2012-09-17于宵晖宋福刚管文强王海勇
于宵晖,宋福刚,管文强,王海勇
0 引言
传统的目标检测方法通常为门限检测,通过降低检测门限增强对微小目标的检测概率,这样势必增加虚警概率。应用 Hough变换方法,将可能是同一目标航迹上的回波能量进行累积,这样增强了信噪比,从而可以对微弱的海面目标进行检测,在一定程度上提高了检测性能。
本文主要研究了基于 Hough变换的低可观测海面运动目标检测算法。首先研究了雷达回波的建模仿真,包括海杂波背景的建模仿真及运动目标的建模仿真,分别比较了高斯(Gauss)分布、对数正态(Log-normal)分布、瑞利(Rayleigh)分布、韦伯(Weibull)分布和K分布在模拟海杂波性能上的优劣。而后介绍了 Hough变换的基本原理,并在此基础上给出基于 Hough变换的直线运动海面目标检测算法。在所研究的算法的基础上,使用Matlab 6.5 提供的用户界面设计工作台,制作出便于用户使用的目标检测综合仿真平台。
1 雷达回波仿真
1.1 海杂波背景的建模仿真
传统上雷达杂波背景分为高斯型和非高斯型两大类。对于低分辨率雷达,杂波由大量基本散射点反射响应构成,幅度服从Gauss分布,接收机包络检波服从Rayleigh分布。随着雷达分辨力和频率的提高或者在低视角观测时,尖杂波使杂波包络的分布相对于 Rayleigh分布有一个长的拖尾。Log-normal分布可以描述海杂波,但是其往往过高估计了实际杂波分布的动态范围,Rayleigh分布模型又对杂波分布动态范围估计不足,Weibull分布较为准确。Log-normal分布和Weibull分布都是两参数分布,其中一个参数是反映杂波平均功率的尺度参数,另一个参数是反映分布偏斜度的形状参数。
在模拟尖海杂波这样的非均匀区域时,K分布比Log-normal和Weibull分布更有效。K分布的复合形式假设每个分辨单元的幅度(散斑分量,speckle)服从高斯分布,方差在时间和空间上服从伽玛(Gamma)分布。这相当于用Gamma分布的随机变量在时间和空间上调制散斑分量的功率。对于低入射余角的雷达海杂波,通常用 K分布作为其幅度分布模型,因为 K分布对观测数据拟合效果较好,而且可以很好的模拟海杂波幅度分布的长尾特性。
以z为随机变量的K分布概率密度函数表示为公式(1)

其中z为海杂波幅度,且0>z;v为形状参数,高分辨低擦地角海杂波31.0<<v;)(⋅Γ是Gamma函数;a是标度函数,与杂波平均值有关。
目前产生相关K分布随机序列主要有两种方法[1]:一种是球形不变随机过程法(SIRP),一种是无记忆非线性变化法(ZMNL)。由于ZMNL方法运算量相对较小并且运用了快速算法,我们采用ZMNL方法对海杂波幅度进行仿真。
1.2 运动目标的建模仿真
在仿真得到的模拟海杂波中加入目标信息即为目标检测所需的雷达回波。本文所讨论目标检测算法中只考虑直线运动的目标信息,因为曲线可以由各个不同时刻的直线无限逼近来近似。只要给出目标运动轨迹的斜率、起始及终止位置坐标、目标信息幅度等参数,即可获得完整的目标信息。
理想的运动目标信息是幅度保持不变的,但实际中,由于雷达接收机的性能等各种原因,目标信息的幅度是不断变化的,一般用 Rayleigh分布来模拟幅度随机变化的目标信息。
2 目标检测
2.1 Hough变换
Hough变换是数据图像处理上用来识别某些图像特征的技术。它通过一种数学上的变换将平面上一点变换为Hough参数空间上的一条曲线。对数据处理而言,Hough变换具有一个很好的特性,即在平面上共线的各点经 Hough变换后,相交于一点。
假定图像数据空间为xoy平面,点(x,y)经Hough变换变换到ρθo平面,得公式(2)

则xoy平面上共线各点变换到Hough参数空间ρθo平面后相交于一点。
[证明]:如图1所示:

图1 Hough变换
得公式(3)

将公式(2)代入公式(3),得公式(4)

平面xoy内直线AB上各点的参量d、α相同,仅1α不同。观察公式(4)可知:
当 αθ=时,d=ρ,即:xoy平面内直线AB经Hough变换后在ρθo平面上相交于),(dα点。[证毕]
每个点经Hough变换后在Hough域内都变为一条正弦曲线,并交于一点,且交点的坐标为xoy平面内直线的两个参量d和α。利用 Hough变换的上述性质,可以把在xoy平面内直线运动目标的回波数据在Hough域内进行加权积累并进行检测,则可通过峰值点坐标得到目标的运动直线轨迹。
2.2 测量数据预处理(第一门限检测)
通过上面的分析我们知道,海杂波背景中有尖峰现象,这种尖峰回波会严重影响我们的目标检测。但从总体上看,除了一些尖峰以外,相当一部分的背景杂波幅度并不大,即回波能量不强。为减少运算量降低虚警概率,本文利用一个预处理门限1l对xoy数据平面图像进行预处理。
采用预处理技术是十分必要的,可以大大减少xoy平面中参与 Hough变换的点数,降低运算量。但是预处理门限并不是提升的越高越好,显见,预处理门限抬高会降低虚警概率,但是同时也会降低检测概率。在实际的 Hough变换检测算法中,应适当选取预处理门限1l的值。
单纯采用门限检测方法对于低信噪比的海面目标检测,效果并不理想,这也是采用 Hough变换的方法进行目标检测的主要原因。
2.3 基于Hough变换的第二门限检测
正如公式(4)所导出的结论。因为xoy数据图像中有一直线运动目标,经 Hough变换加权处理后,在Hough域内有明显尖峰,由此断定雷达回波数据中有目标存在。
因为Hough域中目标回波能量经加权积累,其幅度值远远大于杂波变换后的加权积累幅度值,因此可以采用门限检测实现 Hough域内的高检测概率、低虚警概率。门限检测可以是固定门限检测,即给出一固定门限,将低于这一门限的回波统统滤除掉;也可以采用自适应门限2l进行目标检测,具体确定方法如下:
首先在Hough变换域内对各坐标点(θoρ平面内)所对应的权值求取平均值 u2;然后根据需要的虚警概率、检测概率确定门限 l2=。当信噪比固定时,在一定的虚警概率漏报概率要求下,随着背景杂波幅度变化,u2值在变化,但n不变。因此这里的检测门限 l2是随着不同的雷达数据自适应变化的。关于利用 Hough变换进行目标检测的检测概率,和多目标区分问题[2]中有详细论述,此处不再讨论。
由于计算误差,在xoy平面内直线运动的同一目标经Hough变换检测后呈现相互靠近的一族点。在确定目标航迹的时候,可将这一族点的ρ,θ坐标分别取均值,得到相应的d,α值,并取xoy平面内满足d±∆d和α±∆α的点族重新参加检测。
对 Hough变换结果分别进行固定门限检测与自适应门限检测,然后根据 Hough域内尖峰出现的位置坐标,通过Hough反变换即可得出目标运动轨迹。如果在xoy平面内有多个直线运动目标,则 Hough变换域将会出现多个峰值点,通过Hough反变换也会得出多个目标的运动轨迹。
3 基于Matlab的海面目标检测综合仿真平台
为了使用户对上述算法有更直观的认识并适于实际应用,使用 Matlab提供的图形用户界面专用设计工作台,制作出了目标检测综合仿真平台,如图2所示:

图2 用户平台
3.1 软件介绍
Matlab提供了一个比较完善的设计、修改图形用户界面的专用工作台(Layout Editor), 所有的界面控件如按键、可编辑文本框、坐标轴等只需在对象模板区中选定相应的控件图标,并在设计工作区中拖动鼠标即可获得,并可根据需要通过“属性编辑工具”随意设定控件属性。对于菜单的编辑及界面的整齐化均有相应的“菜单编辑工具”与“对齐工具”等来完成,如图3所示:

图3 设计工作台
从图中可以看出,完成上述操作后,工作台上所制作的界面模型及所含构件已经符合设计要求,但这个界面各构件之间的通讯还没有建立,为此必须使用激活图形工具进行激活处理。激活后,系统会自动生成一个M函数文件,用户只需在相应的回调函数名下填写相应的回调函数,而无需更改其自动生成的程序。经过上述步骤生成的图形用户界面就可以投入使用了。
3.2 功能概述
如图2所示,该界面是实现基于Hough变换的海面运动目标检测仿真平台。用户可根据仿真要求分别选择 K分布、Log-normal分布、Gauss分布或Weibull分布来模拟背景海杂波,并分别选择加入定幅或不定幅的单目标或多运动目标信息,合成含有目标信息的雷达回波。用户也可选择直接读取已有的(真实的或模拟的)含目标信息的雷达回波数据。
界面上的8个坐标系可分别显示背景杂波、加入目标信息后的雷达回波、预处理门限检测后的三维图及平面图、Hough变换后所得到的三维图及对其进行门限检测后所得三维图与平面图、Hough反变换求得的目标航迹8幅图,使用户对目标检测过程与结果有更直观地认识。
用户输入所需参数后,在菜单中选择所要做的目标检测仿真形式及检测方法,程序就会按要求运行并给出检测结果。比如选择 K分布模拟海杂波,加入定幅双目标信息,采用自适应检测方式,则所得的目标检测结果,如图4所示:
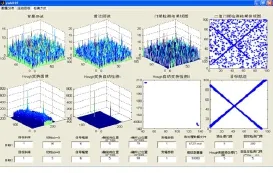
图4 目标检测结果
4 结语
本文在前人研究的基于 Hough变换的低可观测海面运动目标检测算法的基础上,对该算法进行了补充与总结。并在此基础上,制作出适于人机交互的用户平台。
将海杂波视为复合 K分布建模进行处理忽视了海杂波的非线性动力学特性。因此基于上述方法的海杂波建模是有局限性的,在依据其建模特性基础上设计目标检测算法也有待进一步的验证。这也将是海面目标检测技术发展的一个重要的方向,同时也将是下一步需要继续进行的研究。
[1]L.James Marier,Jr.“Correlated K-distributed clutter generation for radar detection and track” [C]IEEE Trans.on Aes.1995.31:568-580
[2]Merrill I. Skonlnik,Radar Handbook [M],New York:McGraw-Hill, 2008:1-20~1-77
[3]刘剑、罗鹏飞、赵艳丽,基于Hough变换的低可观测海面运动目标检测[J],系统工程与电子技术,2004.3;
[4]郭陈林.,基于 Hough变换的微弱目标检测方法研究[D],成都:电子科技大学硕士论文,2011;
[5]夏宇垠、冯大政、李涛,一种基于Hough变换的宽带雷达目标检测器[J],电子与信息学报,2010.11;
