TD-LTE系统中Zadoff-Chu序列的研究与DSP实现*

陈发堂，吴增顺

（重庆邮电大学 通信与信息工程学院，重庆400065）

TD-LTE系统中Zadoff-Chu序列的研究与DSP实现*

陈发堂，吴增顺

（重庆邮电大学 通信与信息工程学院，重庆400065）

通过对Zadoff-Chu(ZC)序列生成算法的分析及理论推导，提出了一种快速、有效的Zadoff-Chu序列生成的DSP实现方案。该方案已经在TMS320C64xDSP中实现。通过在CCS3.3中运行程序，验证了方案的可行性和高效性。该方案在LTE-TDD无线综合测试仪表的开发中已经得到应用。

LTE系统；Zadoff-Chu序列；DSP实现

在TD-LTE系统中，Zadoff-Chu(ZC)序列主要应用于上行RS序列生成、PRACH前导序列生成以及主同步信号生成等[3]，它在整个TD-LTE系统中扮演着重要的角色，是建立上下行链路同步以及信道估计中不可或缺的一部分。Zadoff-Chu序列具有良好的自相关性和互相关性，这有利于减少不同前导之间的相互干扰，而且其本身具有对称性，这有利于减少序列生成的复杂度。同时LTE系统选择了素数长度的Zadoff-Chu序列，保证序列检测性能的提高。

本文通过对ZC序列生成的分析以及自身的特性，结合理论推导，提出了一种简化的ZC生成算法的DSP实现方案，并通过仿真与比较，验证了该方案的可行性，能够满足LTE系统性能的要求。

1 Zadoff-Chu算法分析

其中 n=0，1，2…Nzc-1，u 为正整数。

参数为u，序列长度为Nzc的ZC序列定义为：

每计算一次Xu(n)的值，在求x的计算上就需要3次乘法和一次除法运算。对于长度为Nzc的序列而言，计算所有Xu(n)的指数x需要3×Nzc次的乘法和 Nzc次的除法运算，然后利用式（2）计算每一个Xu(n)的值。

用式(2)计算Zadoff-Chu序列的生成存在两点不足：(1)余弦和正弦运算属于一种非线性的运算，多次运算的复杂度很高，耗时很长，不利于满足LTE系统实时性的要求；(2)MS320C6000系列DSP在软件的实现中只能处理定点数运算，无法直接对浮点数进行处理。因而要利用式(2)计算必须对正弦和余弦进行量化处理。

在定点DSP芯片中，采用定点数进行数值运算，其操作数一般采用整型数表示。一个整型数的最大表示范围取决于DSP芯片所给定的字长，一般为16 bit或32 bit。对DSP芯片而言，参与数值运算的数就是16 bit的整型数。通过设定小数点在16 bit数中的不同位置，就可以表示不同大小和不同精度的小数。数的定标有Q表示法和S表示法两种，如表1所示。

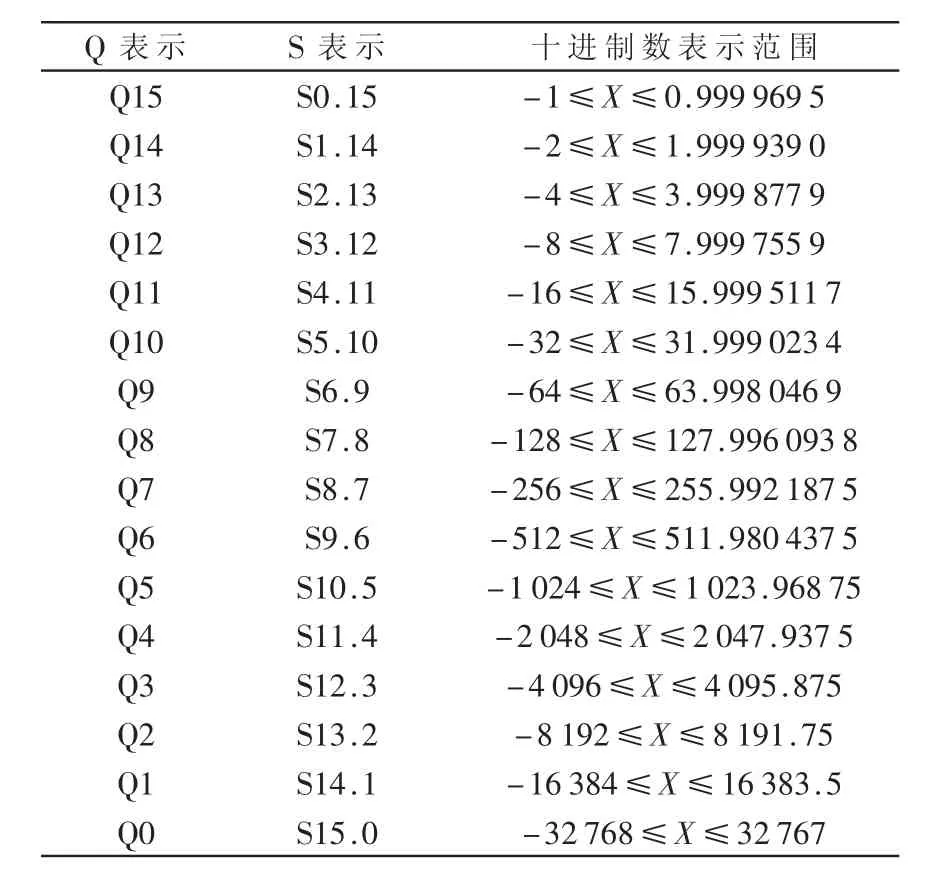
表1 Q表示和S表示及数值范围

从表1可以看出，不同的Q所表示的数不仅范围不同，而且精度也不相同。Q越大，数值范围越小，但精度越高；相反，Q越小，数值范围越大，但精度就越低。本文采用Q量化方法，浮点数与定点数的转换关系可表示为：浮点数(x)转换为定点数(xq)：xq=(int)x×2q

式中int表示下取整。由正弦和余弦的范围，结合表1可知，可以采用Q15进行浮点数到定点数的转化。为了减少正弦和余弦由于非线性造成的复杂运算，可以采用查表的方法。首先对 sin(x)的 0～π的值进行量化处理，根据sin(x)本身的对称性可以通过0～π的量化值取反得到；其次，根据正弦和余弦之间的关系cos(x)=sin(x+π/2)，可以将余弦值的求法转化到求正弦上。由于量化存在着误差，因而量化的点数越多，所求的值越接近理论上的值，但量化点数越大占用的内存空间也越大。在0～π在之间进行2 048点量化时，已十分接近理论值。因此采用0～π在之间进行2 048点量化。进一步对式（1）推导发现：

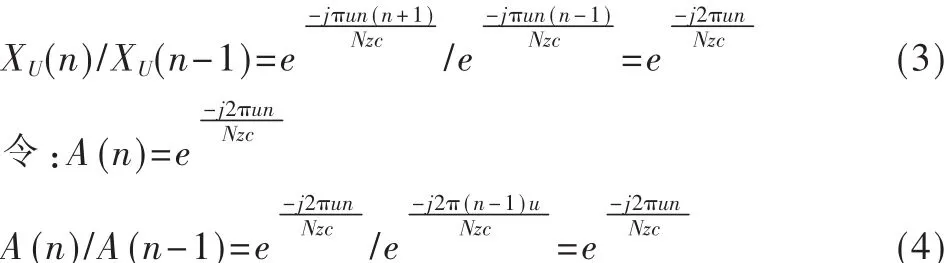
由式（4）可知，对于给定的参数 u，A(n)/A(n-1)为定值，对于初始值 A(0)=1，XU(0)=1。通过式(3)和式(4)的递推关系就可以只通过乘法运算计算出ZC序列，在计算时只需要计算一次正弦和余弦即可。用这种方法将正弦和余弦转化成复数的乘法运算，减少了正弦和余弦归一化和量化查表的时间，进一步降低运算的复杂度。

由ZC序列本身所具有的性质可知：

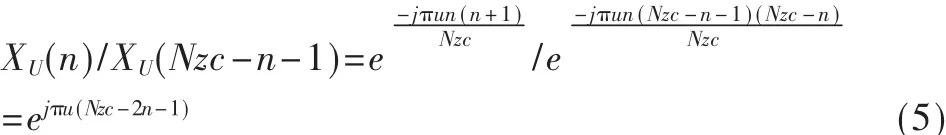
ZC序列是关于序列长度Nzc中心点呈对称性，因此可以利用此性质进一步减少运算的时间。

2 Zadoff-Chu的DSP实现

2.1 硬件

MS320C6000系列DSP是TI公司推向市场的高性能DSP，综合了目前性价比高、功耗低等优点。TMS320C64系列在TMS320C6000×DSP芯片中处于领先水平，它在体系结构上采用了VelociTI甚长指令集VLIW（Very Long Instruction Word）结构[5]，芯片内有 8个独立功能单元的内核，每个周期可以并行执行8条32 bit指令，最大峰值速度为4 800 MIPS，支持8/16/32/40 bit的数据访问。由于其出色的运算能力、高效的指令集及大范围的寻址能力，使其特别适用于测试仪表等对运算能力和存储量有高要求的应用场合。

2.2 Zadoff-Chu序列的DSP实现

因为ZC模块的输入序列长度不尽相同，所以本模块是按给定参数单独处理。ZC算法是作为一个子函数模块，其调用格式为：ZcSequenceGen(int，int，short*)，其中，int分别有2个 int表示 Nzc为输入序列的长度、u为输入序列序列号；short*为ZC_out输出序列的首地址。

具体实现流程描述如下：

(1)初始值 ej2πu/Nzc的量 化处理

由式（6）u除以Nzc，商为m，余数为 k，结合eix的周期性可知，它的值就是u除以Nzc的余数所对应的指数的值。

如果u除以Nzc的余数大于Nzc，用它的余数减去2×Nzc，把它的商的范围变换到（-Nzc，0）上；如果它的商小于 Nzc，则不对u进行处理。将u归一化到（-Nzc，Nzc）之间后，再除以 Nzc，将它变换到（-1，1）之间，因为存储的正弦表的指数x的范围是在（0，π）之间。正弦表的指数 x在（0，π）之间进行 2 048点的采样，把采样的值求出对应的正弦值后用Q15进行量化。将量化之后的值存储在内存中。x/π的范围是在（0，1）之间，1对应的 Q15量化为 32 768，因此，在（0，1）之间进行2048点的采样，采样间隔为32768/2048=16。根据公式cos(x)=sin(x+π/2)可知，ej2πu/Nzc的余弦值是把量化的值加上 16 384。对量化之后的值和加上16384的值首先判断它的正负，如果为负数，则把为负数的值进行取反，如果是正数，则不作处理。然后再用它们处理之后的值除以16，得到商和一个余数，判断余数是否＞8，如果＞8，则商加 1；如果商≤8，则商不变。用得到的商作为查表的偏移量，利用STH指令取出相应量化的值，从而完成了初始值的计算。具体流程图如图1。

(2)ZC序列的计算

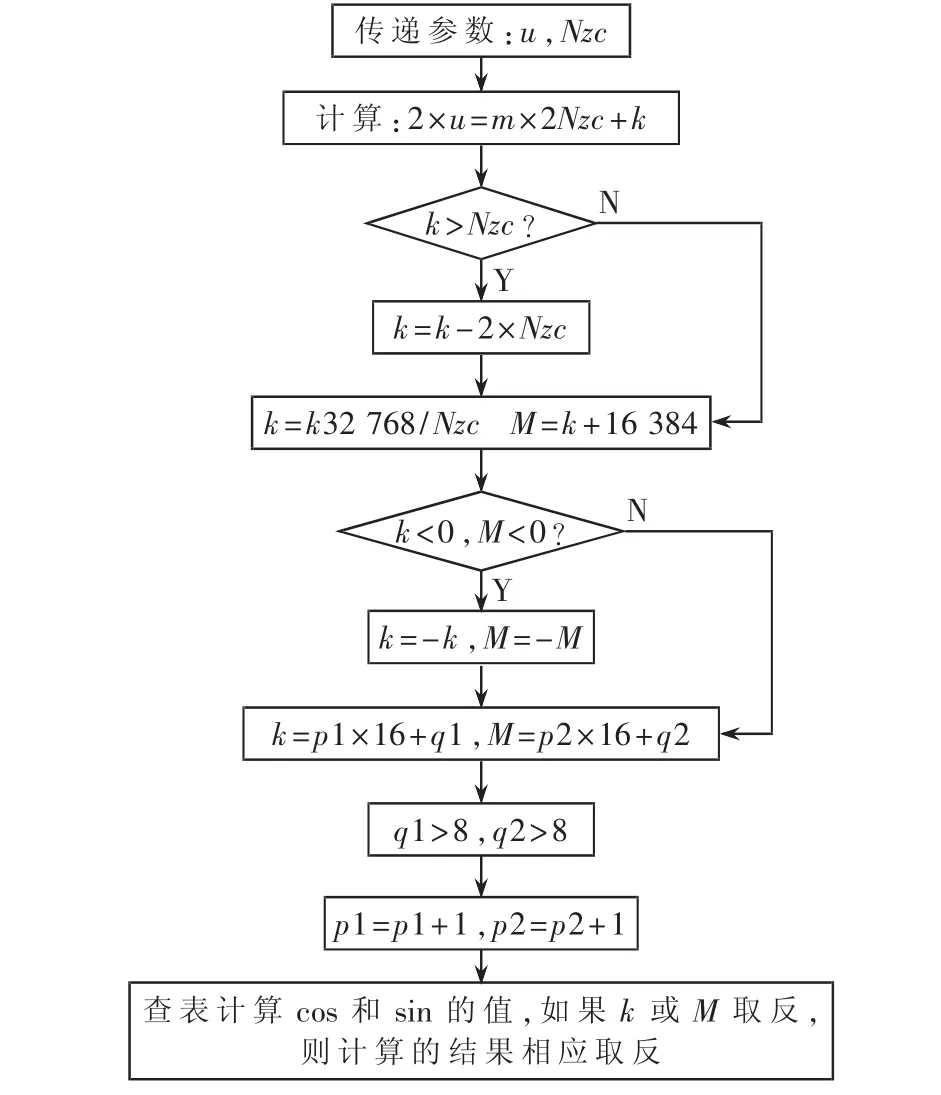
图1 初始值的计算流程

首先把递推公式的初始值A(0)=1和Xu（0）=1分别用MVK指令赋值到相应的寄存器中。由递推关系式，首先计算出 A（n），由于 A（n-1）和计算出的旋转因子 M均为复数，不能直接进行相应的乘法运算，只能采用复数相乘的法则。即A(n)的实部等于A（n-1）和M的实部与虚部分别相乘后再进行相减。为了减少指令的开销，可以采用DOTPN2指令，该条指令可以直接完成A(n-1)的实部和虚部与M的实部和虚部相乘之后相减，把得到的实部用SHR指令进行右移16 bit，保证得到的结果为半字。同样A（n）的虚部的计算，先用汇编指令PACK2交换M的实部和虚部，再用DOTP2指令完成A(n-1)和M的高16 bit和低16 bit的相乘以及A(n-1)和M的低16 bit和高16 bit的相乘之后再相加，同样用SHR指令对虚部的计算结果右移16 bit，保证虚部在半字的范围内。 计算完成 A（n）后，再把 A（n）和 Xu（n-1）进行复数相乘，从而得到 Xu（n）的计算结果。由 ZC序列本身所具有的对称性，分别将计算出的Xu（n）的实部和虚部用STH指令分别压栈到输出结果的第n个字和第Nzc-n-1个字中，至此ZC序列的计算全部完成。

3 性能分析与总结

通过DSP软件实现得到的结果与用MATLAB搭建的链路得到的理论数据进行比较，如图2所示。图2虽然只是长度Nzc=139点，但不失一般性。从图中可以看出，虽然量化误差的存在，但是在 2 048点对 sin在（0，π）区间进行量化时，得到的结果与理论数据的值相差在0.1%左右。同时在应用DSP软件实现中，尽量对程序进行优化，通过指令并行，操作码的合理设计以及减少或消除程序中的’NOP’指令[6]等方法进行优化。当运用TMS320C64×DSP芯片实现时，由于处理器的超高主频一般为1 GHz，所以一个指令周期耗时为1 ns，其运算速率非常快，如表2所示，与直接进行ZC序列的生成相比较大大降低了运算时间，可以满足LTE系统的快速有效性。

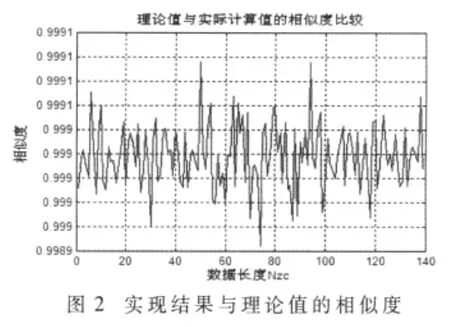
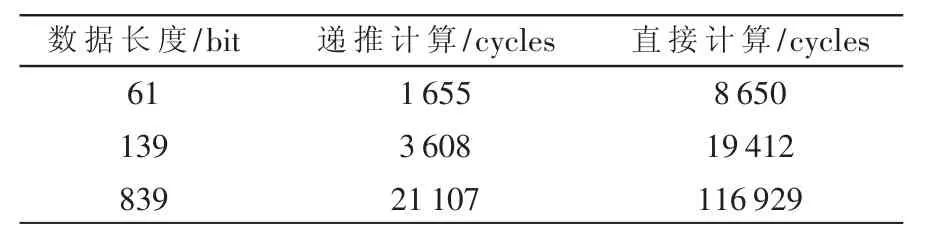
表2 计算量的比较

本文从理论分析出发，根据TD-LTE系统特性以及Zadoff-Chu序列本身的性质，提出了一种简单有效的Zadoff-Chu算法实现方案，并将该算法在TMS320C64×芯片上实现。程序运行结果表明，提出的算法具有可行性和高效性，能够满足TD-LTE系统的需求。该方案已在LTE-TDD无线综合测试仪表的开发中得到了应用。

[1]丁玉美.数字信号处理[M].西安：西安电子科技大学出版社，2002.

[2]何方白，张德民.数字信号处理[M].北京：高等教育出版社，2009.

[3]3GPP TS 36.211 v9.0.0 Evolved universal terrest-rial radio access(E-UTRA)physical channels and modulation(release 9)[S].2009-12.

[4]SAIDI A.Decimation-in-time-frequency FFT algorithm,Manuscript，To be published.1993(8).

[5]Texas Instruments Incorporated.TMS320C64x/C6-4x+DSP.CPU.and.Instruction.Set.Reference.Guide[E-B/OL].Http://www.ti.com.cn,2008.

[6]Texas Instruments Incorporated.TMS320C6000系列 DSP编程工具与指南[M].田黎育，何佩琨，朱梦宇，译.北京：清华大学出版社，2006：32-50.

[7]冯侨，邓娟，沈静，等.LTE系统中ZC序列的实现方法[P]：CN 101826890 A.2010.09.08.

Research and DSP realization of Zadoff-Chu sequence in TD-LTE system

Chen Fatang，Wu Zengshun
(School of Communication and Information Engineering,Chongqing University of Posts and Telecommunications,Chongqing 400065，China)

Analysis and research on the Zadoff-Chu sequence generation algorithm Principles[3，7],a fast and effect DSP implementation approach is proposed in this paper and implemented in the TMS320C64xDSP.The running results of the ZC sequence generation program in CCS3.3 verifies that the program is feasible and effective.The program has been applied to the development of LTE-TDD wireless integrated test instrument.

TD-LTE system；Zadoff-Chu sequence；DSP realization

TN929.5

A

0258-7998(2012)03-0041-03

国家科技重大专项,TD-LTE无线综合测试仪表开发（2009ZX3002-009）

2011-11-01)

陈发堂，男，1965年生，副教授，硕士生导师，主要研究方向：TD-LTE系统开发。

吴增顺，男，1987年生，硕士研究生，主要研究方向：TD-LTE系统物理层算法及DSP软件开发。