VDP方程在Simulink仿真中的解析
2012-09-15巴合提古丽阿斯里别克孙迎春
巴合提古丽·阿斯里别克,王 颖,孙迎春
(1.东北师范大学物理学院,吉林 长春 130024;2.新疆伊犁师范学院电子与信息工程学院,新疆 伊犁 135000;3.吉林大学数学学院,吉林 长春 130012)
Simulink是用来对动态系统实现建模、进行仿真和分析的一个软件包.它是MATLAB的一个重要的组成部分.利用Simulink可以建立更趋于真实的非线性模型,如考虑空气阻力和摩擦中的各个干扰因素等.另外,Simulink系统建造的自定义用户模块对设计系统及分析结论的正确性都具有非常重要的意义.因此,Simulink软件的功能已经成为专业技术人员必须掌握的一项技能.
在系统所受的非线性阻尼作用所引起的非线性中范德玻尔(Van der Pol)方程是最简单而最典型的非线性方程[1].其数学方程式为

在范德玻尔方程中,增加外力Vcosωt项,其变成强迫范德玻尔方程,其数学方程式为
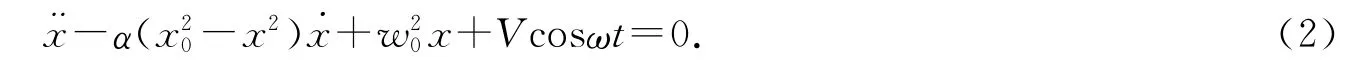
其中:V为外力的振幅;ω为角频率.其描述的系统叫自激振荡系统.
1 范德玻尔方程的Simulink仿真
自激系统是一种在非线性阻尼作用下振动的系统,对范德玻尔方程而言,从机械振动的角度来看,-α-x2)是可变的阻尼系数.其中当|x|>|x0|时阻尼系数为正数,则系统会受阻尼作用,能量将逐渐减少;但当|x|<|x0|时阻尼系数为负数,这样系统的能量不仅不降低反而增加.结果系统在自动反馈调节系统的作用下做稳定的周期振荡,系统在一个振荡过程中消耗的能量正好等于补充的能量.
强迫范德波尔方程在不同的参数条件下显示不同的吸引子,即1周期吸引子、2周期吸引子、不变环吸引子和奇怪吸引子[1-3].本文采用Simulink仿真通过时间历程图和相图显示系统取不同参数下的振荡行为和相应的吸引子形状.
1.1 建立Simulink仿真模型

相加点(Sum)模块:此模块的对话框中符号“list of signs”设置为“-,+,-”,“Icon shape”选为rectangular.
增益(Gain)模块:在模块参数设置对话框中2个增益模块的“Gain”参数分别设置为a和w.
积分(Integrator和Integrator1)模块:可以完成初值设定,采用对参数对话框中“Initial condition”的设置,在Integrator模块中设置˙x的初值为4,Ingegrator1模块中设置x的初值为4.
点乘(Product)模块:对话框的“Number of inputs”设置为2(表示有2个输入端).
函数功能(Fcn)模块:对话框的“Expression”设置为“1-u*u”(等于公式中的1-x2).
函数(Trigonometric Function)模块:对话框的“Function”设置为cos.
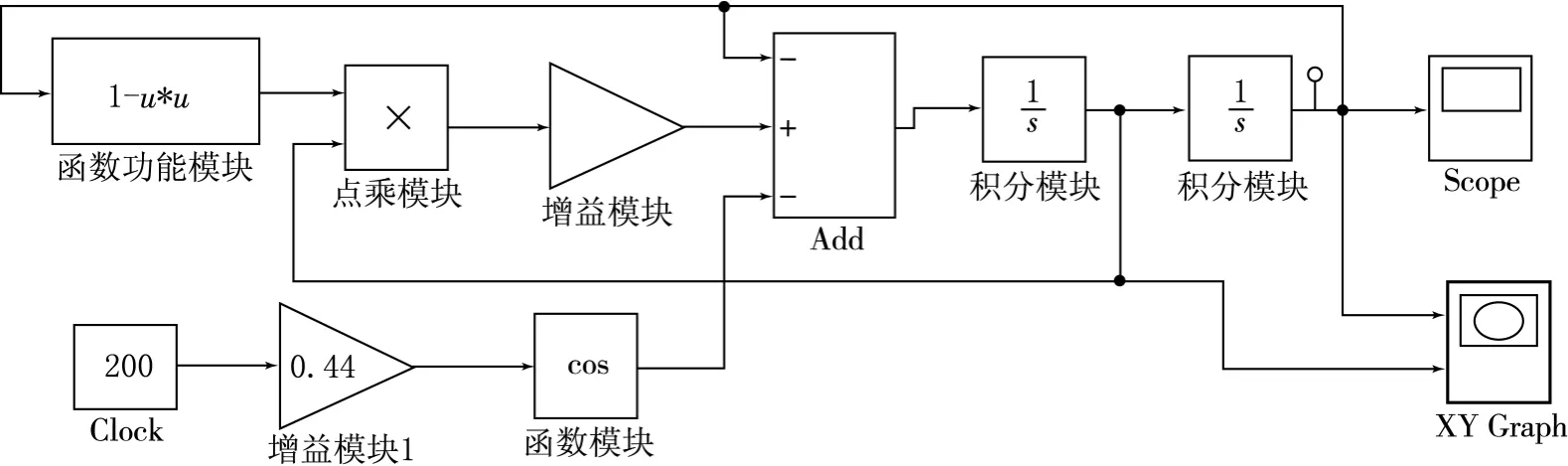
图1 范德波尔方程的仿真模型
1.2 查看Simulink仿真结果
仿真操作时对增益模块给出不同的参数值,可以得到不同的结果,直到找到理想的结果为止,通过Scope和XY Graph模块查看.
(1)在a=0.79,w=0.44条件下,出现1周期吸引子,此时系统的周期等于外驱动力的周期,系统做主谐波运动,如图2所示.

图2 强迫范德玻尔方程中a=0.79和w=0.44时的相图和位移曲线图
(2)在a=0.99,w=0.44条件下,系统的周期等于外驱动力的整数倍,出现2周期吸引子,系统做次谐波运动,如图3所示.
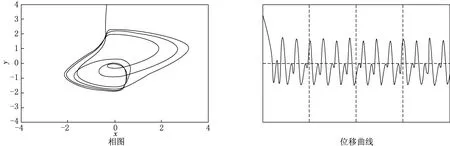
图3 强迫范德玻尔方程中a=0.99和w=0.44时的相图和位移曲线图
(3)在a=0.66,w=0.44条件下,出现不变环吸引子,系统做准周期运动,如图4所示.
(4)在a=1.08,w=0.44条件下,出现奇怪吸引子,表示系统做混沌运动,如图5所示.
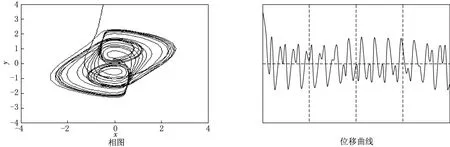
图4 强迫范德玻尔方程中a=0.66和w=0.44时的相图和位移曲线图
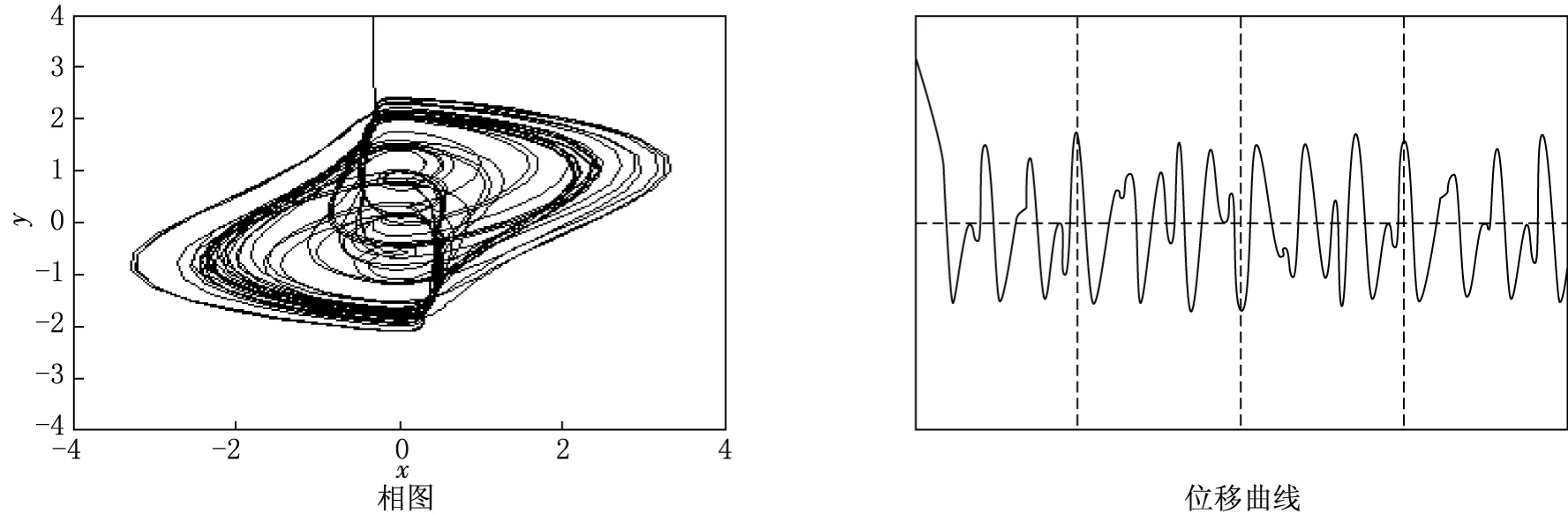
图5 强迫范德玻尔方程中a=1.08和w=0.44时的相图和位移曲线图
2 系统的封装
以上仿真系统的模块数量比较多,系统规模比较大,系统的操作也比较复杂.我们每次设置参数时都要打开2个增益模块输入参数值,如果对这个系统采用封装子系统技术,系统的操作就变得更方便,规模也变得更简单.所谓的封装子系统技术就是把系统的相关的模块集合在一起变成一个模块,把各模块的参数设置对话框合成一个参数对话框[8],生成的子系统模块功能等效于原系统模块群的功能.
2.1 封装步骤
(1)创建一个子系统:模型中选择要建立的子系统除了输入端和出口端以外的所有模块,单击Edit菜单中Create Subsystem命令即可,可用一个模块代替所选中的所有模块.
(2)创建封装系统:选中生成的Subsystem模块(子模块),单击Edit菜单中Mask Subsystem命令,这时会弹出封装编辑器(Mask editor)对话框.
(3)对封装系统进行编辑:通过(Mask editor)对话框上面的4个选项卡(分别为设置封装模块图标、设置封装子系统参数和初始化命令、设置模块帮助和说明)进行编辑,完成封装子系统.
2.2 具体操作步骤
(1)创建子系统模型:选中除了Scope模块和XY Graph模块以外的全部模块→单击Edit菜单中的Create Subsystem命令(也可右击选中部位),即可创建一个子系统(如图6所示).
(2)创建封装子系统模块图标:选中子系统模块→右击弹出下拉菜单→单击Mask Subsystem命令→弹出“Mask editor”对话框→在对话框中选Icon项→在Drawing commands框中可输入disp(‘VDP’),并可设置Icon options各项.
(3)封装子系统参数的设置:选中“Mask editor”对话框中的Parameters项→添加自激系统的2个变量即2个参数.在第一行的Prompt栏目中输入该变量的提示信息,如“阻尼系数”,在Variable栏目中输入相关联的变量名a,注意该变量名必须和模型中的完全一致.Type栏目选择为Popups,并在Popups栏目中填写a的4个值(每行填一个值).填第2个参数时,提示信息是“角频率”,变量名是w,Type栏目是默认值为edit,表示用编辑框来接收数据.
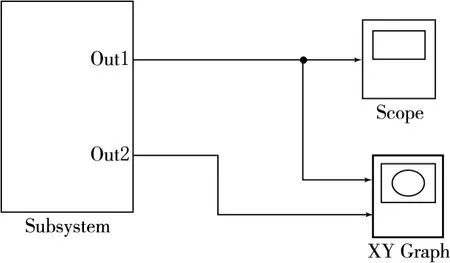
图6 子系统模型
(4)初始化设置:在此可以用“Mask editor”对话框中的Initialization项定义封装然后用子系统工作空间中的各种变量来设置初始化命令.
(5)设置模块帮助和说明:在模块编辑器中选中编辑选项卡Domumentation项→在编辑框中可输入模块类型、模块描述、模块帮助的说明.如在 Mask description中可以这样说明,this is a VDP function example.
(6)通过单击Ok命令来完成子系统的封装设置,形成封装系统,如图7所示.
双击该子系统模块,在弹出的参数设置对话框中可直接设置系统的2个变量a和w的值(如图8所示).
运行仿真系统,通过Scope和XY Graph模块即可查看跟以上一致的计算结果.
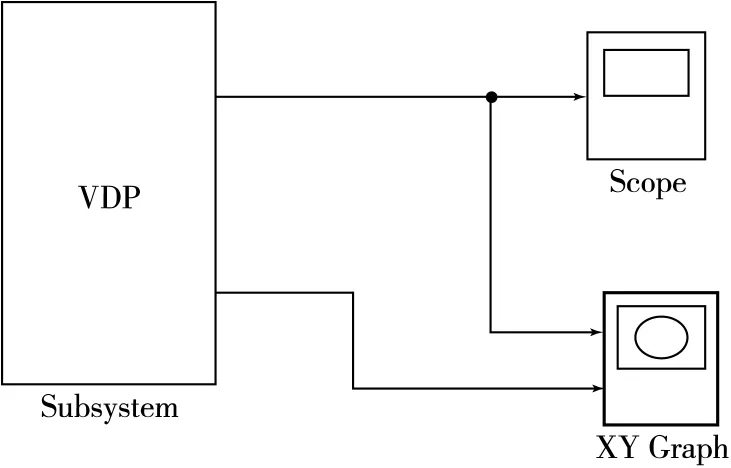
图7 强迫范德玻尔方程的子系统模型
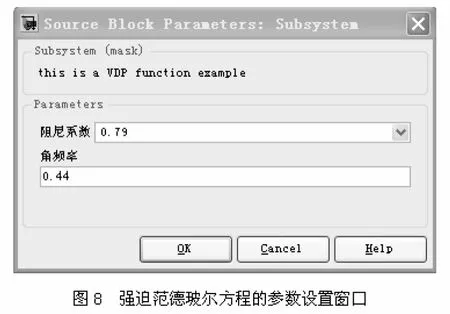
图8 强迫范德玻尔方程的参数设置窗口
3 小结
本文通过对范德玻尔方程的数学模型的分析,建立了自激系统的Simulink仿真系统,即二阶常微分方程的基本仿真模型,考虑了模型中二阶常微分方程的初始条件,演示了二阶常微分方程仿真模型的子系统封装过程,并通过实例验证了仿真结果的正确性,从而使仿真过程变得更加简便,结果表明:在解决二阶常微分方程中使用Matlab/Simulink仿真方法能提供一个良好的用户使用界面,通过这个用户使用界面,用户可以客观的操作系统的具体行为并能得到及时的结果.
[1]刘秉正,彭建华.非线性动力学[M].北京:高等教育出版社,2001:120-209.
[2]彭芳麟,管靖,胡静,等.理论力学计算机模拟[M].北京:清华大学出版社,2002:192-197.
[3]刘秉正.非线性动力学与混沌基础[M].长春:东北师范大学出版社,1994:1-407.
[4]李颖,朱伯立,张威.Simulink动态系统建模与仿真基础[M].西安:西安电子科技大学出版社,2004:129-278.
[5]高智中,韩新风,章毛连.一个新的四维超混沌系统及其电路仿真[J].东北师大学报:自然科学版,2012,44(1):77-83.
[6]吴晓强,陈彩云,岳立娟.一类参数不确定时滞混沌系统的反同步[J].吉林大学学报:理学版,2011,49(5):922-929.
[7]许永红,温朝晖,莫嘉琪.一类 Lorenz系统的变分迭代解法[J].吉林大学学报:理学版,2011,49(1):51-55.
[8]姚俊,马松辉.Simulink建模与仿真[M].西安:西安电子科技大学出版社,2002:5-182.
