关于n长路的（a，b；n）－优美标号

马凤敏，吴晓春，张 伟，张庆成

（1.河北工业职业技术学院基础部，河北 石家庄 050000；2.东北师范大学数学与统计学院，吉林 长春 130024）

1 预备知识

对于一个图G（V，E），如果对每一个v∈V（G），存在一个非负整数g（v）（称为顶点v的标号）满足：（1）max｛g（v）｜v∈V｝＝｜E（G）｜；（2）∀u，v∈V，如果u≠v，则g（u）≠g（v）；（3）∀e1，e2∈E（G），如果e1≠e2，则g＊（e1）≠g＊（e2），其中g＊（e）＝｜g（u）－g（v）｜，uv＝e（称为由g导出的边标号），则称G为优美图，称g为G的一个优美值或优美标号.设Pn是一个n长路，其上的点依次为v0，v1，…，vn，a和b是非负整数，若Pn的优美标号g 满足g（v0）＝a，g（vn）＝b，则称g是Pn的一个（a，b；n）－优美标号，记为g（a，b，n），称Pn是（a，b；n）－优美的.

优美标号的概念是由Golomb在文献［1］中给出的.由于应用范围的广泛性，许多学者做了大量的研究工作，已有详尽的研究成果［2］.2004年，P.Gvozdjak在文献［3］中为了解决著名的Oberwolfach问题，提出（a，b；n）－优美猜想：路Pn是（a，b；n）－优美的当且仅当非负整数a，b，n满足：（1）b－a与n（n＋1）／2有相同的奇偶性；（2）0＜｜b－a｜≤（n＋1）／2；（3）n／2≤a＋b≤3n／2.

该猜想的必要性已由P.Gvozdjak在文献［3］中给出.关于充分性，文献［3］对n≤20的情况验证成立.a＝0的情况，S.M.Lee等人在文献［4］给出.a＝1，2的情况由文献［5］解决了.a＝3的情况我们已另文证明.本文则证明了a＝4时，（a，b；n）－优美猜想成立.

为方便我们约定，Z表示整数集，Z［m，k］＝｛x∈Z｜m≤x≤k｝，当k＞m 时，记Z［m，k］＝∅.

2 结果及证明

我们首先利用非负整数a，b，n满足（a，b；n）－优美猜想条件，把n和b进行分类.

引理2.1 当a＝4，非负整数a，b，n满足（a，b；n）－猜想条件，则

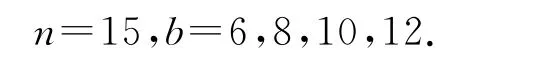
n≥16，b＝（n－7）／2或b＝（n－3）／2或b＝（n＋1）／2或b＝（n＋5）／2或b＝（n＋9）／2.

引理2.2 当a＝4，n为偶数时，该猜想成立.即对满足猜想条件的b和偶数n，Pn是（4，b；n）－优美的.

证明思路是将部分特殊值具体标出，一般情形对n分情况进行处理.

证明 a＝4.

当n≥16时，把n分成5种情况讨论：

情形1 当n≡0（mod 10）.

当n≥40时，我们定义v1，v2，…，v10（3＋m）的优美标号g如下：

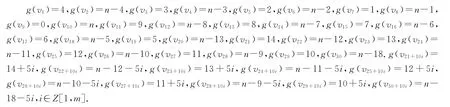
（1）当b＝（n－8）／2，m＝n／10－4，我们定义vn－9，vn－8，…，vn＋1的优美标号g如下：

（2）当b＝（n－4）／2，m＝n／10－4，我们定义vn－9，…，vn－8，vn＋1的优美标号g如下：

（3）当b＝n／2，m＝n／10－4，我们定义vn－9，vn－8，…，vn＋1的优美标号g如下：

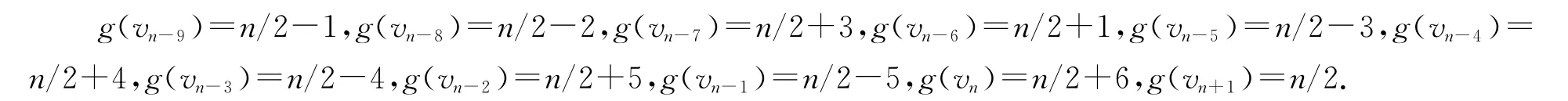
（4）当b＝（n＋4）／2，m＝n／10－5，我们定义vn－19，vn－18，…，vn＋1的优美标号g如下：

（5）当b＝（n＋8）／2，m＝n／10－4，我们定义vn－9，vn－8，…，vn＋1的优美标号g如下：

情形2 当n≡2（mod 10）.

当n≥42时，我们定义Pn的（4，b；n）－优美标号如下：

（1）顶点v1，v2，…，v10（3＋m）的优美标号g与情形1给定的g 相同.

（2）当b＝（n－8）／2，m＝（n－2）／10－4，我们定义vn－11，vn－10，…，vn＋1的优美标号g如下：

（3）当b＝（n－4）／2，m＝（n－2）／10－4，我们定义vn－11，vn－10，…，vn＋1的优美标号g如下：

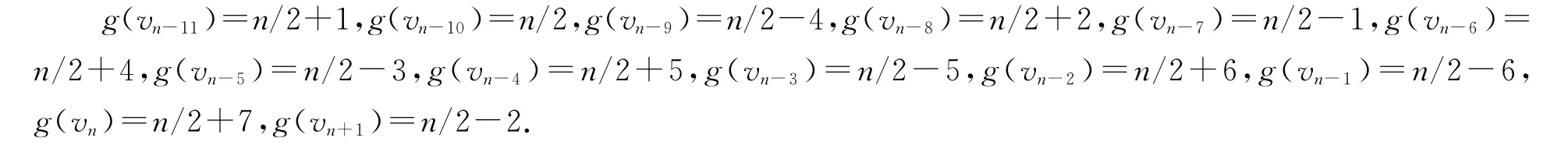
（4）当b＝n／2，m＝（n－2）／10－4，我们定义vn－11，vn－10，…，vn＋1的优美标号g如下：

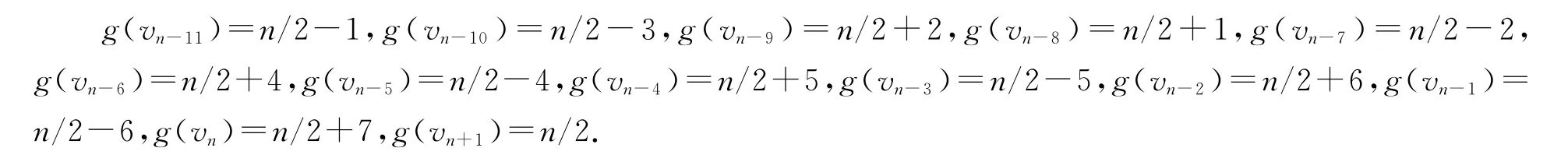
（5）当b＝（n＋4）／2，m＝（n－2）／10－4，我们定义vn－11，vn－10，…，vn＋1的优美标号g如下：

（6）当b＝（n＋8）／2，m＝（n－2）／10－4，我们定义vn－11，vn－10，…，vn＋1的优美标号g如下：

情形3 当n≡4（mod 10）.

当n≥44时，我们定义Pn的（4，b；n）－优美标号如下：

（1）顶点v1，v2，…，v10（3＋m）的优美标号g与情形1给定的g 相同.

（2）当b＝（n－8）／2，m＝（n－4）／10－4，我们定义vn－13，vn－12，…，vn＋1的优美标号g如下：

（3）当b＝（n－4）／2，m＝（n－4）／10－4，我们定义vn－13，vn－12，…，vn＋1的优美标号g如下：

（4）当b＝n／2，m＝（n－4）／10－3，我们定义vn－3，vn－2，…，vn＋1的优美标号g如下：

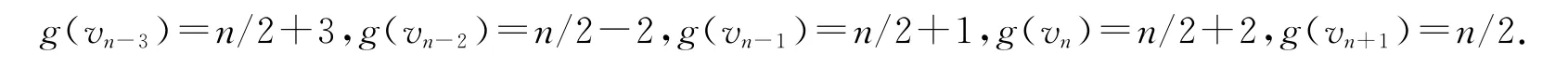
（5）当b＝（n＋4）／2，m＝（n－4）／10－3，我们定义vn－3，vn－2，…，vn＋1的优美标号g如下：

（6）当b＝（n＋8）／2，m＝（n－4）／10－5，我们定义vn－23，vn－22，…，vn＋1的优美标号g如下：

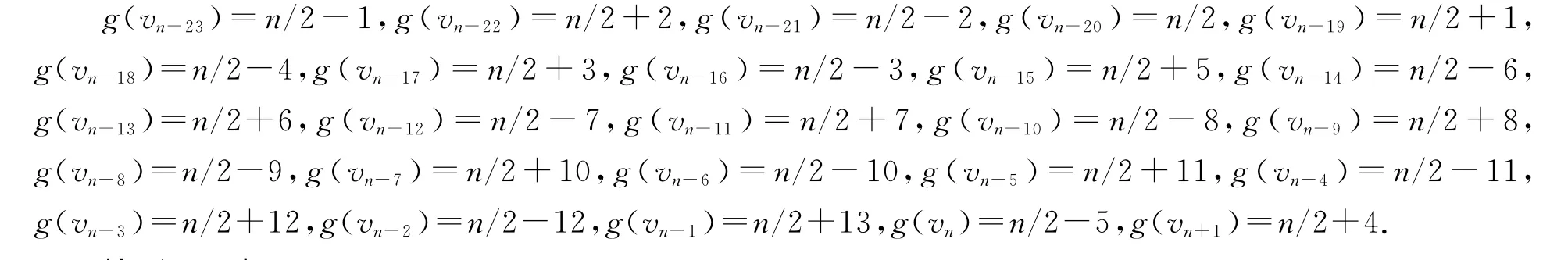
情形4 当n≡6（mod 10）.

当n≥46时，我们定义Pn的（4，b；n）－优美标号如下：

（1）顶点v1，v2，…，v10（3＋m）的优美标号g与情形1给定的g 相同.

（2）当b＝（n－8）／2，m＝（n－6）／10－4，我们定义vn－15，vn－14，…，vn＋1的优美标号g如下：

（3）当b＝（n－4）／2，m＝（n－6）／10－3，我们定义vn－5，vn－4，…，vn＋1的优美标号g如下：

（4）当b＝n／2，m＝（n－6）／10－4，我们定义vn－15，vn－14，…，vn＋1的优美标号g如下：

（5）当b＝（n＋4）／2，m＝（n－6）／10－3，我们定义vn－5，vn－4，…，vn＋1的优美标号g如下：

（6）当b＝（n＋8）／2，m＝（n－6）／10－3，我们定义vn－5，vn－4，…，vn＋1的优美标号g如下：

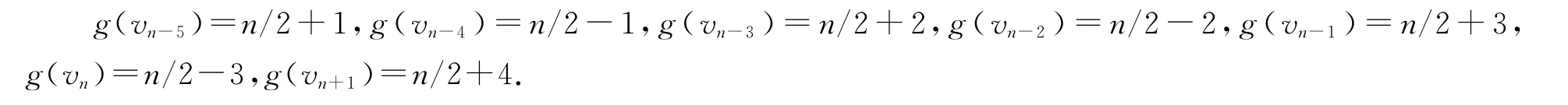
情形5 当n≡8（mod 10）.

当n≥38时，我们定义Pn的（4，b；n）－优美标号如下：

（1）顶点v1，v2，…，v10（3＋m）的优美标号g与情形1给定的g 相同.

（2）当b＝（n－8）／2，m＝（n－8）／10－3，我们定义vn－7，vn－6，…，vn＋1的优美标号g如下：

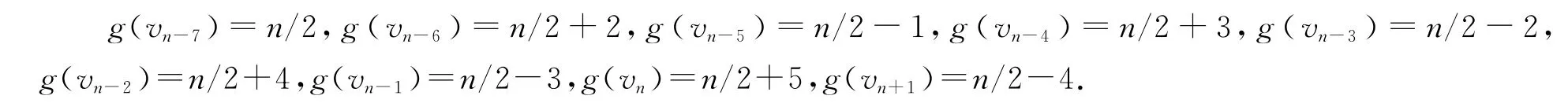
（3）当b＝（n－4）／2，m＝（n－8）／10－3，我们定义vn－7，vn－6，…，vn＋1的优美标号g如下：

（4）当b＝n／2，m＝（n－8）／10－3，我们定义vn－7，vn－6，…，vn＋1的优美标号g如下：

（5）当b＝（n＋4）／2，m＝（n－8）／10－3，我们定义vn－7，vn－6，…，vn＋1的优美标号g如下：

（6）当b＝（n＋8）／2，m＝（n－8）／10－3，我们定义vn－7，vn－6，…，vn＋1的优美标号g如下：

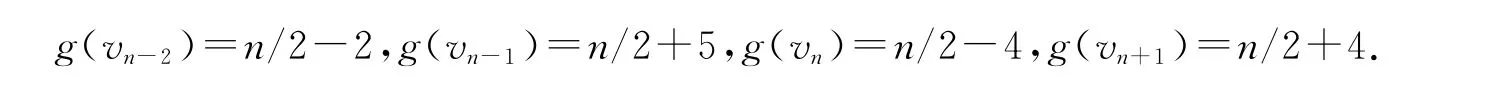
引理2.3 当a＝4，n为奇数时，（a，b；n）－优美猜想成立.即对满足猜想条件的b和奇数n，Pn是（4，b；n）－优美的.当n≥16，我们分以下5种情形分别讨论：

情形1 n≡1（mod 10）.

当n≥41时，我们定义Pn的（4，b；n）－优美标号如下：

（1）顶点v1，v2，…，v10（3＋m）的优美标号g与引理2.2情形1给定的g相同.

（2）当b＝（n－7）／2，m＝（n－1）／10－4，我们定义vn－10，vn－9，…，vn＋1的优美标号g如下：

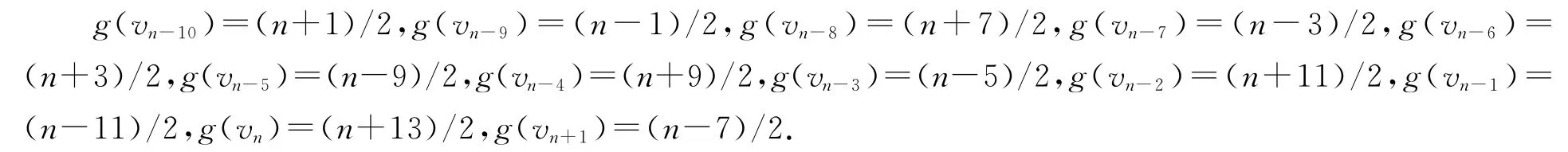
（3）当b＝（n－3）／2，m＝（n－1）／10－4，我们定义vn－10，vn－9，…，vn＋1的优美标号g如下：

（4）当b＝（n＋1）／2，m＝（n－1）／10－4，我们定义vn－10，vn－9，…，vn＋1的优美标号g如下：

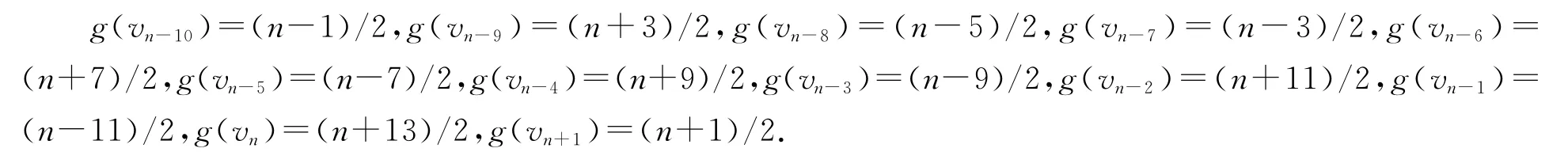
（5）当b＝（n＋5）／2，m＝（n－1）／10－5，我们定义vn－20，vn－19，…，vn＋1的优美标号g如下：

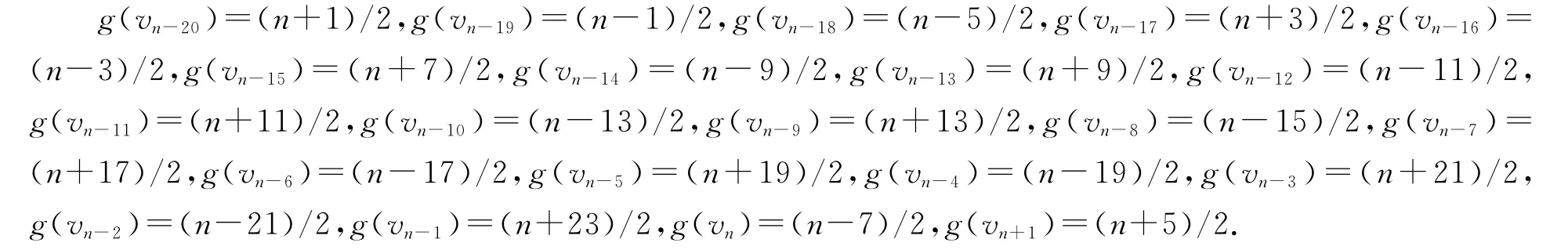
（6）当b＝（n＋9）／2，m＝（n－1）／10－4，我们定义vn－10，vn－9，…，vn＋1的优美标号g如下：

情形2 当n≡3（mod 10）.

当n≥43，我们定义Pn的（4，b；n）－优美标号如下：

（1）顶点v1，v2，…，v10（3＋m）的优美标号g与引理2.2情形1给定的g相同.

（2）当b＝（n－7）／2，m＝（n－3）／10－4，我们定义vn－12，vn－11，…，vn＋1的优美标号g如下：

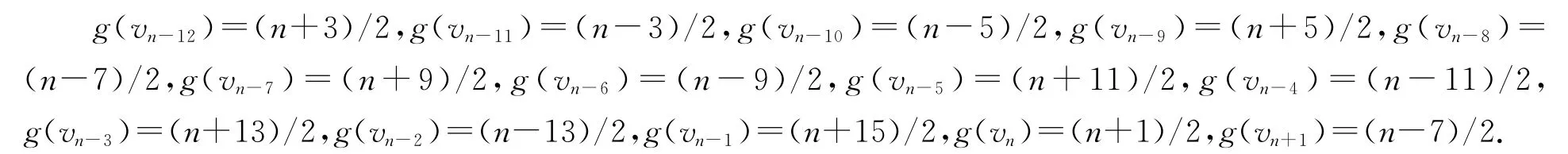
（3）当b＝（n－3）／2，m＝（n－3）／10－4，我们定义vn－12，vn－11，…，vn＋1的优美标号g如下：

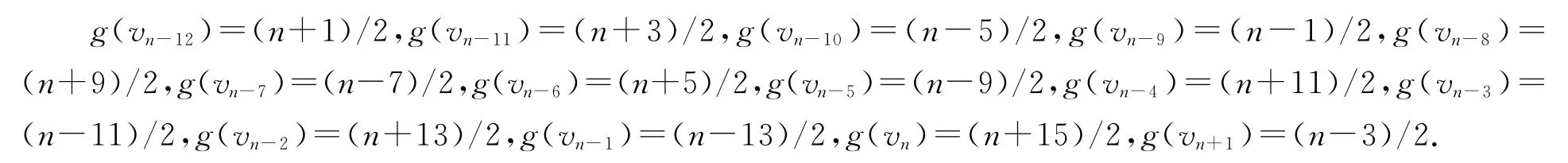
（4）当b＝（n＋1）／2，m＝（n－3）／10－4，我们定义vn－12，vn－11，…，vn＋1的优美标号g如下：

（5）当b＝（n＋5）／2，m＝（n－3）／10－4，我们定义vn－12，vn－11，…，vn＋1的优美标号g如下：

（6）当b＝（n＋9）／2，m＝（n－3）／10－4，我们定义vn－12，vn－11，…，vn＋1的优美标号g如下：

情形3 当n≡5（mod 10）.

当n≥45时，我们定义Pn的（4，b；n）－优美标号如下：

（1）顶点v1，v2，…，v10（3＋m）的优美标号g与引理2.2情形1给定的g相同.

（2）当b＝（n－7）／2，m＝（n－5）／10－4，我们定义vn－14，vn－13，…，vn＋1的优美标号g如下：

（3）当b＝（n－3）／2，m＝（n－5）／10－3，我们定义vn－4，vn－3，…，vn＋1的优美标号g如下：

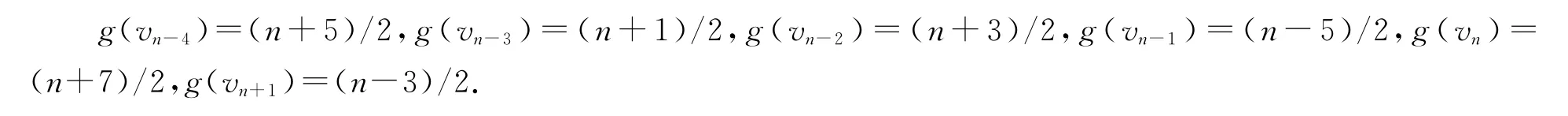
（4）当b＝（n＋1）／2，m＝（n－5）／10－3，我们定义vn－4，vn－3，…，vn＋1的优美标号g如下：

（5）当b＝（n＋5）／2，m＝（n－5）／10－3，我们定义vn－4，vn－3，…，vn＋1的优美标号g如下：

（6）当b＝（n＋9）／2，m＝（n－5）／10－5，我们定义vn－24，vn－23，…，vn＋1的优美标号g如下：

情形4 当n≡7（mod 10）.

当n≥47，我们定义Pn的（4，b；n）－优美标号如下：

（1）顶点v1，v2，…，v10（3＋m）的优美标号g与引理2.2情形1给定的g相同.

（2）当b＝（n－7）／2，m＝（n－7）／10－3，我们定义vn－6，vn－5，…，vn＋1的优美标号g如下：

（3）当b＝（n－3）／2，m＝（n－7）／10－3，我们定义vn－6，vn－5，…，vn＋1的优美标号g如下：

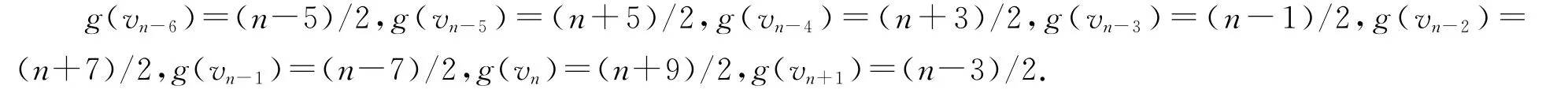
（4）当b＝（n＋1）／2，m＝（n－7）／10－4，我们定义vn－6，vn－5，…，vn＋1的优美标号g如下：

（5）当b＝（n＋5）／2，m＝（n－7）／10－3，我们定义vn－6，vn－5，…，vn＋1的优美标号g如下：

（6）当b＝（n＋9）／2，m＝（n－7）／10－3，我们定义vn－6，vn－5，…，vn＋1的优美标号g如下：

情形5 当n≡9（mod 10）.

当n≥39，我们定义Pn的（4，b；n）－优美标号如下：

（1）顶点v1，v2，…，v10（3＋m）的优美标号g与引理2.2情形1给定的g相同.

（2）当b＝（n－7）／2，m＝（n－9）／10－3，我们定义vn－8，vn－7，…，vn＋1的优美标号g如下：

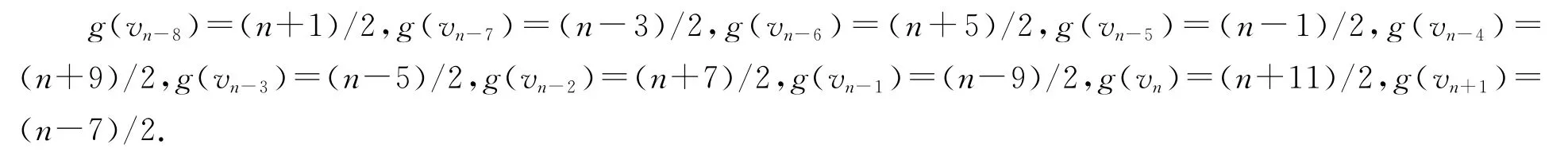
（3）当b＝（n－3）／2，m＝（n－9）／10－3，我们定义vn－8，vn－7，…，vn＋1的优美标号g如下：

（4）当b＝（n＋1）／2，m＝（n－9）／10－3，我们定义vn－8，vn－7，…，vn＋1的优美标号g如下：

（5）当b＝（n＋5）／2，m＝（n－9）／10－3，我们定义vn－8，vn－7，…，vn＋1的优美标号g如下：

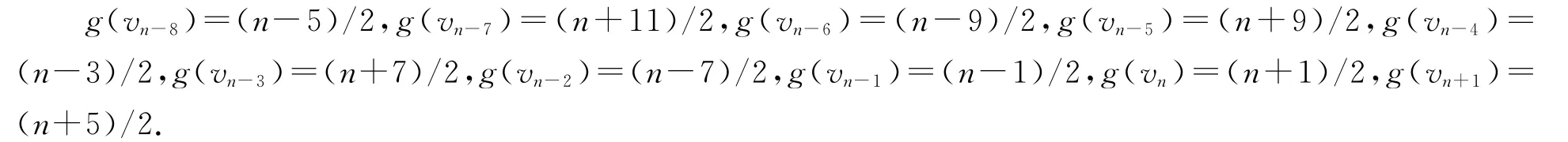
（6）当b＝（n＋9）／2，m＝（n－9）／10－3，我们定义vn－8，vn－7，…，vn＋1的优美标号g如下：

由引理2.1—2.3可得本文主要结果：

定理2.1 当a＝4时，（a，b；n）－优美猜想成立.即对满足猜想条件的b，n，Pn（n≥4）是（4，b；n）－优美的.

［1］GOLOMB S W.How to number a graph，in graph theory and computing［M］.New York：Acadmic Press，1972：23－37.

［2］GALLIAN J A.A dynamic survey of graph labeling［J］.The Electronic Journal of Combinarorics，2009（DS6）：1－219.

［3］GVOZDJAK P.On the oberwolfach problem for cycles with multiple lengths［D］.Burnaby：Simon Fraser University，2004.

［4］LEE S M，LAI K Y，WANG Y S.On the graceful permutation graphs conjecture［J］.Congressus Numerantium，1994，103（2）：193－201.

［5］范丽霞，梁志和.关于n长路的（a，b；n）－优美猜想［J］.河北师范大学学报：理学版，2010，34（1）：5－9.