孔隙压力精确预测方法及其在九龙山地区的应用
2012-09-15赵忠文李黔黄桢米光勇
赵忠文李 黔黄 桢米光勇
1.西南石油大学石油工程学院 2.中国石油西南油气田公司川西北气矿
孔隙压力精确预测方法及其在九龙山地区的应用
赵忠文1李 黔1黄 桢2米光勇2
1.西南石油大学石油工程学院 2.中国石油西南油气田公司川西北气矿
赵忠文等.孔隙压力精确预测方法及其在九龙山地区的应用.天然气工业,2012,32(6):65-68.
四川盆地川西北地区九龙山构造具有多套产层,纵向上存在多套压力系统且含有异常高压。因地层孔隙压力预测不准确导致的井下复杂与事故(井漏、井涌、溢流、卡钻),给该区的安全、快速钻井施工带来了很大的困难。为此,基于九龙山地区已完钻井的测井资料,在常规孔隙压力预测模型的基础上,运用切比雪夫逼近原理建立最佳一致逼近的多项式模型对实际地层孔隙压力进行多次逼近,通过确定最佳值一致逼近多项式的关键系数,进而建立起了具备地质构造特点的地层孔隙压力精确预测模型。应用结果表明,这种全新的预测方法建立的地层孔隙压力剖面具有相当高的吻合率,成功实现了对九龙山构造异常地层压力的精确预测。
四川盆地 川西北地区 九龙山构造 孔隙压力 精确计算 切比雪夫最佳一致逼近
地层孔隙压力数据作为一项描述地质环境的关键数据,对于建立钻井液安全密度窗口有着非常重要的作用。实现对四川盆地川西北地区九龙山构造的孔隙压力精确预测对于改善钻井设计、指导安全钻进,从而为避免钻井复杂事故的发生,实现安全、快速、高效的钻井施工有着重要的意义[1]。
1 切比雪夫最佳一致逼近原理
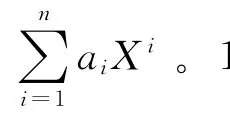
切比雪夫逼近理论在解决工程问题上已经有了非常多的应用,例如应用切比雪夫多项式来解决岩土力学参数概率的分布、黑体辐射以及雷达散射截面上的问题[6-8];切比雪夫最佳一致逼近理论隶属于函数逼近论的范畴,从根本上理解就是研究数据与数据之间的近似表达问题;而传统模型进行地层孔隙压力预测的研究思路是真实地层压力数据与原始测井数据之间的近似表达,因此这一目的与切比雪夫最佳一致逼近理
论是相符合的。
2 孔隙压力精确计算模型
2.1 精确计算模型原理
按照切比雪夫提出的最佳一致逼近思想,利用n次多项式模型总是可以对任意的函数进行逼近,虽然最佳一致逼近的方法切比雪夫并未提及。对实际地层孔隙压力的研究应用中,我们知道对某一固定的地质特征构造而言,测井响应与实际的地层孔隙压力有直接函数关系,目前的研究来看,这种函数关系就是我们现有的计算模型。但是由于模型自身的缺陷,对于孔隙压力的预测会出偏差。因此,利用切比雪夫的逼近思想,建立最佳一致逼近的多项式模型对实际地层孔隙压力进行多次逼近,逼近多项式的自变量为传统模型计算出的地层孔隙压力,通过确定最佳值一致逼近多项式的关键系数,最终建立具备地质构造特点的地层孔隙压力精确预测模型。
这套模型是对实际地层孔隙压力的最佳逼近,因此这套模型具有了地质构造特点,如果某一区块没有在地质构造上没有发生突变,那么这套精确计算模型就可以应用于其他相近的邻井的地层孔隙压力预测。地层孔隙压力的精确预测原理如图1所示。
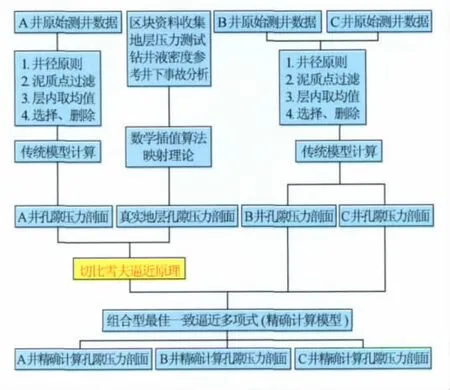
图1 孔隙压力精确计算原理图
2.2 精确计算模型建立方法
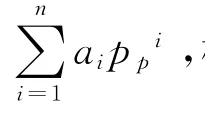
3.1.2 膀胱穿孔 膀胱穿孔是TURBT需要特别警惕的并发症,术前应常规进行CT/MRI扫描,了解肿瘤浸润深度和基底大小。电切过深、膀胱过度充盈及闭孔反射是穿孔的主要原因,电切时膀胱灌入液体不能太多,以免膀胱过度膨胀,使膀胱壁变得太薄而容易穿孔;电切侧壁肿瘤时需警惕闭孔反射发生,切除侧壁肿瘤前,可适当加深麻醉予以肌松剂甚至闭孔神经阻滞,适当充盈膀胱,甚至请手术助手适当固定同侧下肢,电切时尽量采取间歇式触发电切模式,均可能降低由于闭孔反射导致的膀胱穿孔发生。此外,术中应仔细辨认结构,一旦切除组织底部见到脂肪组织时,提示已经穿孔,应立即停止这一区域的电切。
3 川西北九龙山井区实例应用
3.1 九龙山构造概况介绍
九龙山构造属四川盆地川北低平褶皱带,龙门山—米仓山山前断褶构造亚带九龙山—张家碥构造群南部的一个局部构造。川北低平褶皱带位于四川盆地西北部,其西北部和北部紧邻龙门山推覆构造带和米仓山台缘隆起带,东南与川中隆起带相邻,龙门山—米仓山山前断褶构造亚带位于该构造带的西北部。
九龙山构造具有多产层、多压力系统、异常高压等特点,钻井中复杂事故多和钻井速度低的问题十分突出,如井涌、溢流、井漏、卡钻、遇阻等复杂情况甚至钻井事故,给川西高压区块的钻井工程带来了诸多困难,阻碍了该区块油气勘探开发的进程和经济效益的提高。
3.2 精确计算模型建立
为了试验精确计算模型的准确性,分别选取已经具备测井资料的3口相邻的龙B井、龙C井、龙A井进行计算。龙A、龙B、龙C井的井口坐标位置很接近,井位所处的地质构造特点也相似,因此可以很好的验证试验的结果。由于龙A井的测井数据较为齐全,因此选取龙A井和收集的真实地层孔隙压力进行切比雪夫多次逼近,生成组合形式的最佳一致逼近多项式。再将生成的最佳一致逼近多项式模型分别对龙B井与龙C井进行精确计算,分别对比传统模型[2-3]和精确计算模型对真实孔隙压力的累积偏差。
对比研究发现,将传统模型计算的龙A井孔隙压力剖面与收集的真实孔隙压力剖面进行多次逼近可以获得以组合形式存在的最佳一致逼近多项式,即孔隙压力精确计算模型
i=1
将利用传统模型(等效深度模型)建立的地层孔隙压力剖面带入到上面的组合型逼近多项式进行连续3次的逼近计算,可获得精确计算后的压力系数剖面,如表2所示。
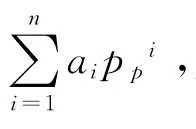

表1 龙A井建立的精确计算模型系数表
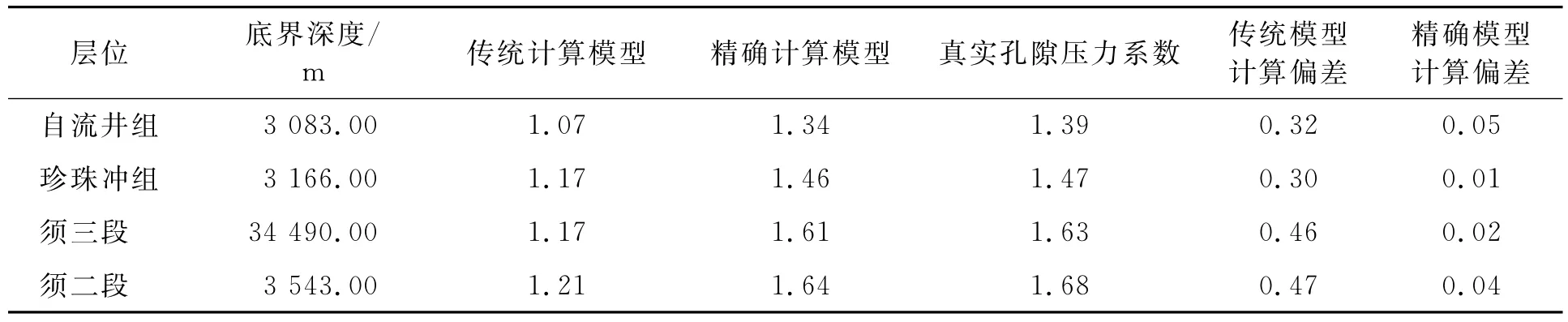
表2 龙A井按地质分层计算孔隙压力系数数据表
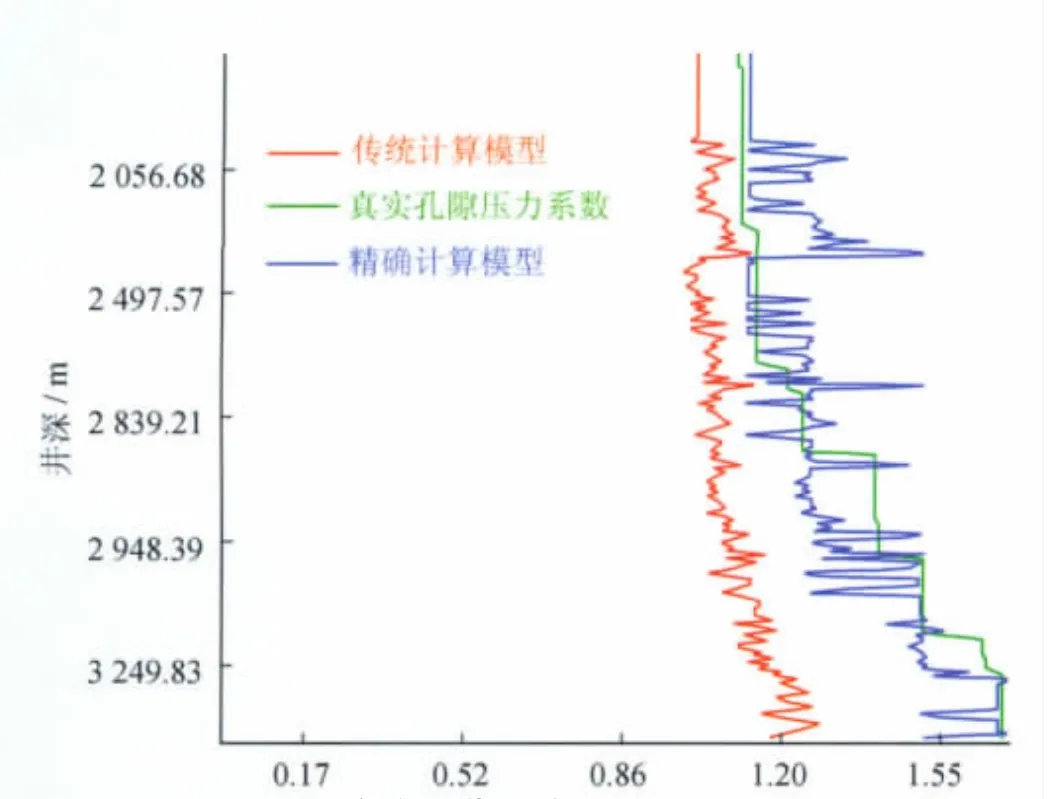
图2 龙A井3个方法获取的孔隙压力剖面对比图
3.3 利用精确计算模型对其他邻井进行计算
为了进一步验证精确计算模型的适用性,分别选取将龙B井、龙C井进行精确地层孔隙压力预测。首先将利用传统模型(等效深度模型)分别建立的龙B井、龙C井的孔隙压力系数剖面(表3、4),再将孔隙压力剖面分别带入到表1建立的精确计算模型,得到精确计算后的地层压力系数剖面(图3、4)。
观察发现,龙B井由传统模型计算的孔隙压力系数地质误差为0.21~0.50,而经过精确计算模型所建立的孔隙压力系数剖面与真实地层孔隙压力系数地质误差仅为0.02~0.06;龙C井由传统模型计算的孔隙压力系数地质误差为0.32~0.50,而经过精确计算模型所建立的孔隙压力系数剖面与真实地层孔隙压力系数地质误差仅为0.01~0.02,小于天然气钻井井控要求钻井液密度附加值0.07~0.15 g/cm3,满足了平衡钻井对地层压力预测精度的要求。
4 结论
1)直接利用传统模型对某一区块进行地层孔隙压力预测精度不高,特别是对于具有复杂地层压力系统的区块传统模型预测结果误差很大,应该充分利用已有的钻井成果数据或实测地层压力数据作为参考,对传统模型计算出的结果数据进行修正。
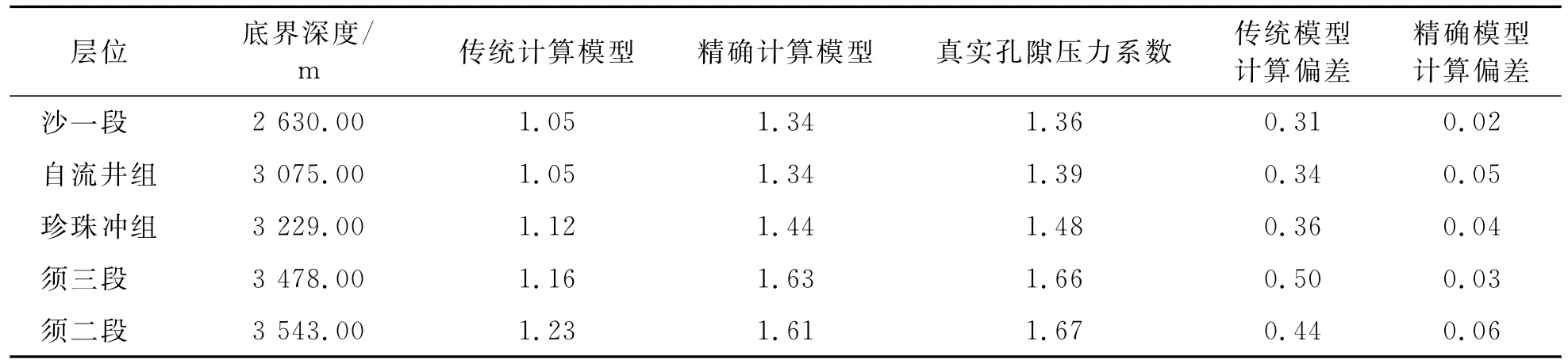
表3 龙B井按地质分层计算孔隙压力系数数据表
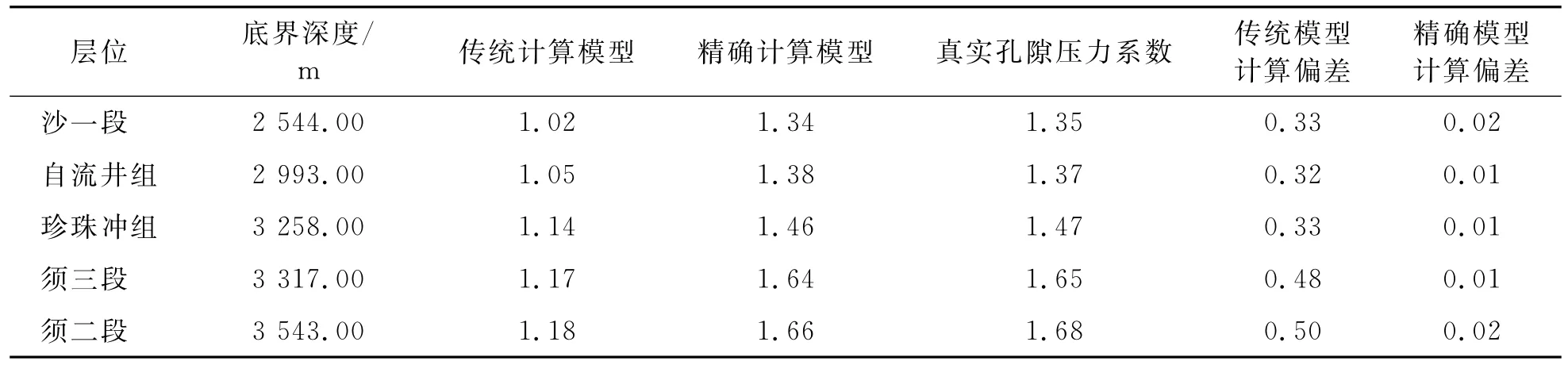
表4 龙C井按地质分层计算孔隙压力系数数据表
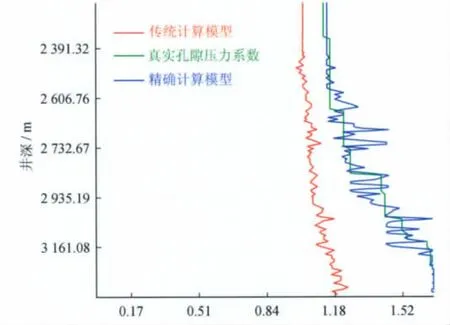
图3 龙B井3个方法获取的孔隙压力剖面对比图
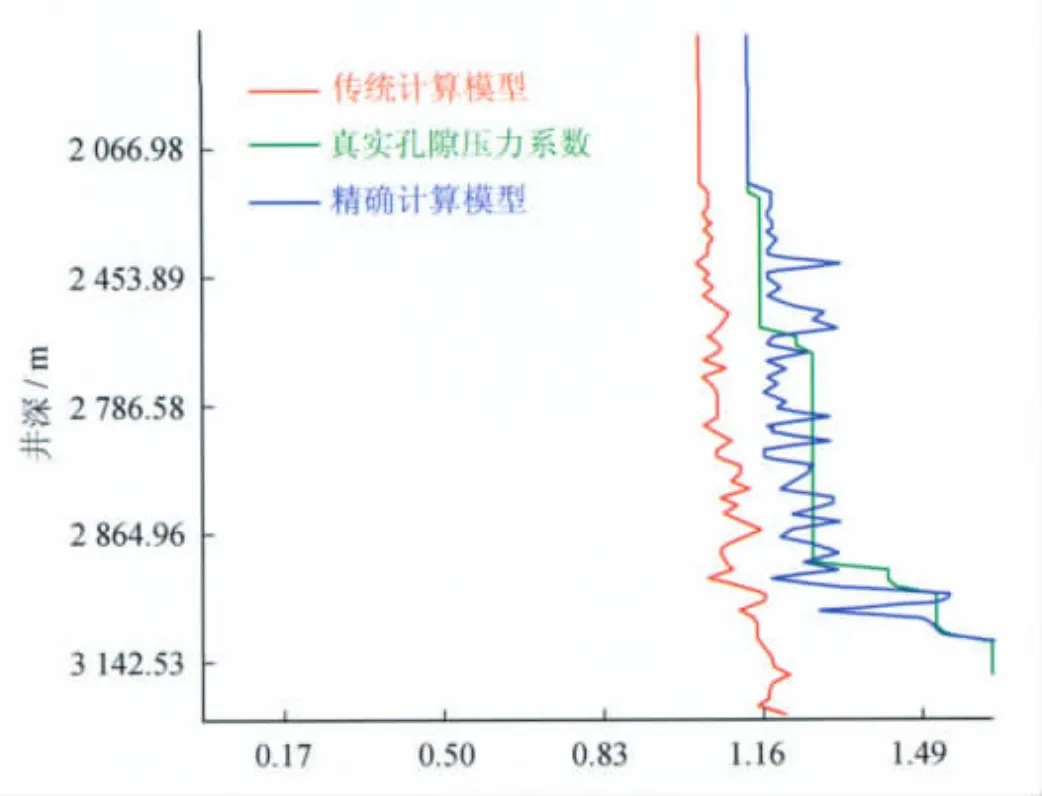
图4 龙C井3个方法获取的孔隙压力剖面对比图
2)利用切比雪夫逼近原理建立的九龙山构造孔隙压力的精确计算模型,通过对邻井的试验发现精确计算模型的计算结果与实际地层孔隙压力吻合度极高。
3)精确计算模型生成的压力剖面具备区块地质特性,能精确地预测相同构造内的地层孔隙压力,对于出现地质构造突变的情况,精确计算模型的精度会受到影响。
[1]唐兴波,李黔,蒋祖军,等.低渗气藏溢流关井孔隙压力计算方法探讨[J].天然气工业,2007,27(3):77-79.
[2]李忠慧,楼一珊,王兆峰,等.地层压力预测技术在准噶尔盆地钻井中的应用[J].天然气工业,2009,29(8):66-68.
[3]张辉,高德利.钻头下部未钻开地层的孔隙压力随钻预测[J].天然气工业,2005,25(3):79-80.
[4]刘学鹏,徐传胜.圣彼得堡数学学派的学术风格探析[J].西北大学学报:自然科学版,2009,39(6):955-959.
[5]于亚萍,李冱岸.Besov函数类的宽度问题[J].中国科技信息,2008,20(20):47-49.
[6]陈钰杰,罗玛.多项式数值逼近法在黑体辐射问题反演中的应用[J].中山大学研究生学刊:自然科学版,2007,28(2):37-43.
[7]宫凤强,李夕兵,邓建.岩土力学参数概率分布的切比雪夫多项式推断[J].计算力学学报,2006,23(6):722-727.
[8]陈明生,孙玉发.应用切比雪夫逼近快速求解目标宽带雷达散射截面[J].电波科学学报,2006,21(4):536-540.
(修改回稿日期 2012-04-16 编辑 凌 忠)
10.3787/j.issn.1000-0976.2012.06.016
国家科技重大专项课题“大型油气田及煤层气开发”(编号:2011ZX05021-006)。
赵忠文,1986年生,硕士研究生;主要从事地质力学模型计算以及复杂井钻完井工艺方面的研究工作。地址:(610500)四川省成都市新都区新都大道8号西南石油大学硕2009级三班。电话:18615781312。E-mail:zzwoo7@163.com
