具有单向离合器的多楔带附件驱动系统旋转振动建模及参数优化设计

张少飞，上官文斌，曾祥坤

(华南理工大学 机械与汽车工程学院，广州 510641)

单根多楔带附件驱动(Serpentine Belt Accessory Drive，简称SBAD)系统由于其结构紧凑、传递功率大、振动和噪声小等优点，逐渐取代了传统的V－带传动，在发动机前端附件驱动系统上得到了越来越广泛的应用［1－3］。

SBAD系统通常由驱动轮、多楔带、若干从动轮和张紧器(包括张紧臂、张紧轮和弹簧阻尼元件)组成［1］，其旋转振动的动态特性包括:轮和张紧臂的角度波动、带段的动态张力、带－轮之间的滑移。SBAD系统中，各从动轮的转动惯量大小不一。一些从动轮所带动的附件由于转速高、转动惯量大(例如发电机轮所带的发电机的转子)，其等效转动惯量在所有从动轮中往往是最大的，对整个SBAD系统旋转振动的动态特性的影响很大［6］。为了降低大惯量附件对SBAD系统旋转振

1 SBAD系统旋转振动建模及动态特性求解

为更好地说明问题的本质，本文仅以由主动轮、从动轮、张紧器组成的三轮－带系统为研究对象，其中，从动轮上有单向离合器装置。通过建立该系统的非线性旋转振动数学模型，给出了从动轮和张紧臂角度波动的数值计算方法，以及各带段动态张力、带－轮间滑移率的求解方法。动的动态特性的影响，常在从动轮与附件之间安装单向离合器(One-Way Clutch，简称单向离合器)［2］。轮与附件间通过单向离合器、扭转弹簧相连，将SBAD系统与大转动惯量的附件之间进行解耦，从而改善SBAD系统的旋转振动特性［7］。

图1 三轮－带SBAD系统结构示意图Fig.1 Schematic of a three pulley-belt SBADs

目前发表的有单向离合器装置的带传动系统建模方面的论文较少。Balaji等［8］建立了有单向离合器装置的七轮－带SBAD系统非线性旋转振动数学模型。根据系统运行时单向离合器装置的结合、分离两种不同状态，将系统看成分段线性系统，采用四阶Runge-Kutta法求解系统响应。Zhu等［9］建立了有单向离合器装置的两轮－带传动系统(由一个主动轮和一个从动轮组成)非线性旋转振动数学模型，并用谐波平衡法分析单向离合器弹簧刚度、系统激励幅值、附件轴与从动轮的转动惯量比对系统动态特性的影响。

本文建立了有单向离合器装置的三轮－带SBAD系统(由一个主动轮、一个从动轮、一个张紧器和一根多楔带组成)的旋转振动数学模型。考虑了带的蠕变、带的阻尼及各轮轴处阻尼的作用。在单谐波激励下，采用Gear数值解法，计算和对比分析了从动轮有、无单向离合器装置对系统动态特性的影响;计算和研究了单向离合器的弹簧刚度，及附件轴与从动轮转动惯量比对系统动态特性的影响。文中还建立了单向离合器弹簧刚度、附件轴转动惯量两系统参数的优化设计数学模型，计算、对比分析了优化前后系统的动态特性。结果表明，优化后的系统参数，三轮－多楔带传动系统的动态特性均得到一定程度的改善。文中单向离合器装置三轮－多楔带传动系统的建模、动态特性求解和参数优化设计的方法，为发动机前端附件驱动系统的旋转振动控制提供了参考。

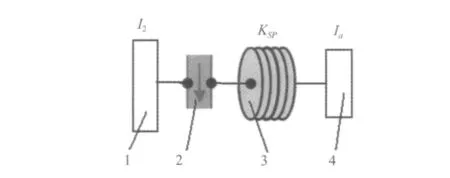
图2 从动轮与其附件轴连接示意图Fig.2 Schematic of the connection in OWC

1.1 旋转振动系统的建模

有单向离合器装置的三轮－带SBAD系统结构示意图见图1:该系统中包括主动轮1、从动轮2、张紧轮3和张紧臂等元件;主动轮顺时针旋转，通过多楔带驱动从动轮和张紧轮;从动轮通过单向离合器、扭转弹簧、与附件轴相连，其连接示意图见图2。

图1中，θi为张紧臂的转角;(Xi，Yi)为张紧臂支点坐标;Li，Ii分别为张紧臂的长度和张紧器绕其支点旋转的转动惯量;(Xi，Yi)(i=1，2，3)为轮 i旋转中心坐标;Bi(i=1，2，3)表示带段 i;Ri，θi，Ii(i=1，2，3)分别为轮i的半径、转角和绕其旋转中心的转动惯量;θa，Ia分别为附件轴的转角和附件轴绕其旋转轴中心的转动惯量;KSP为单向离合器的弹簧刚度。另外，张紧器的动态力学特性参数用弹簧刚度Kt和等效粘性阻尼C表示。

模型假设［1－6］:带的物理特性一致，以准静态方式伸缩;除张紧轮外，其它轮和张紧臂作定轴转动;带在轮上不发生滑移;不考虑带旋转振动与带横向振动(垂直于带的速度方向)的耦合。利用Hamilton原理建立从动轮、附件轴、张紧轮及张紧臂的运动方程分别为:

(1)从动轮运动方程:

(2)附件轴运动方程:

(3)张紧轮运动方程:

方程(1)～(3)中，Qi(i=2，3)为轮 i的负载;Ci(i=1，2，3)为各轮旋转轴处的粘性阻尼(Ci=0.006 Nm·s)［10］;g(δθ)为单向离合器弹簧扭矩，其计算式为:

其中:δθ为从动轮与附件轴的转角差(即δθ=θ2－θa)。

为方便对系统动态响应进行迭代求解，将单向离合器弹簧扭矩用双曲正切函数表达成连续函数的形式，即 g(δθ)=0.5KSPδθ［1+tanh(εδθ］，ε 取 10 000［9］。

方程(1)、(3)中，Ti为带段i的张力，其计算式为:

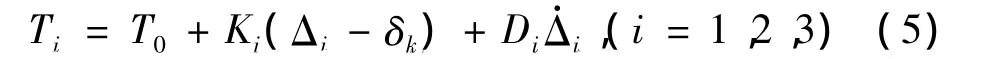
式中:T0为带的初始张力;Ki为带段i的纵向弹性刚度，Ki=EA/Li，其中EA为带的纵向弹性模量;Di为带段i的阻尼，Di=ηKi，η为带的阻尼刚度比，η取0.001 2［11］。式(6)中，KP(i)=EA/(Riβi)为轮 i包角处带段的弹性刚度，βi为带在轮i上的包角。

(4)张紧臂运动方程:

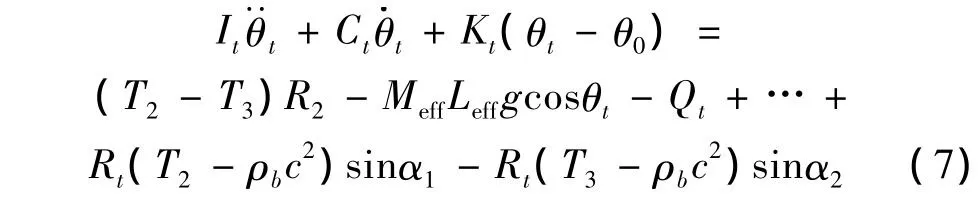
其中:Meff为张紧器总质量;Leff为张紧器质心到张紧臂支点的长度;Qt为张紧器弹簧的预载;θ0为张紧器的安装角度，定义为系统静态时正X方向逆时针旋转到张紧臂的转角;ρb为带的线密度;c为皮带纵向运动的速度;αi(i=1，2)为张紧臂与张紧轮相邻带段的夹角(见图1)，其表达式为:

其中:Li(i=1，2，3)为带段 Bi(i=1，2，3)的长度。L2，L3及张紧轮中心坐标(X3，Y3)均为张紧臂角度 θt的函数:

1.2 系统动态特性的求解

由方程(1)～(3)、(7)描述的系统运动方程为非线性常微分方程组，可采用数值解法求解系统的动态响应。本文采用Gear数值解法(以下简称Gear法)计算系统动态响应，相对4－5阶Runge-Kutta数值解法，Gear法能更快地得到方程的解［5］。

设系统中各元件的动态响应x=［θt，t，θ2，2，θa，a，θ3，3］T，将动态响应初始值x0=［θ0，0，0，0，0，0，0，0］T代入与 Gear法对应的ode15s函数中，可计算出系统各元件的动态响应。其中，θ0为张紧臂的初始角。

在求出系统的动态响应后，将各轮的角度和角速度波动值代入由式(5)、式(6)组成的方程组中，可以算出所有带段的动态张力。

带－轮间的滑移率用带与轮之间的相对速度来描述，其计算式为［13］:

其中，Γi为带与轮i间的滑移率;VB为带的纵向速度，由于张紧轮上没有负载的作用，VB可用张紧轮节圆半径上的线速度来表示，即VB=3R3，其中3为张紧轮的角速度;Vi为轮i节圆半径上的线速度，Vi=iRi，其中i为轮i的角速度。

2 SBAD系统旋转振动动态特性分析

张紧器参数对SBAD系统旋转振动特性的影响已有研究［10－12］。因此，本节的主要内容是计算和研究有/无单向离合器装置，及单向离合器的附件轴与从动轮转动惯量比(以下简称惯量比，用α表示，α=Ia/I2，Ia为单向离合器附件轴的转动惯量)和弹簧刚度对SBAD系统旋转振动动态特性的影响。

2.1 系统模型参数

系统激励为主动轮的角度波动(单位为rad)。假设主动轮转速为500 r/min时，主动轮的角度波动为0.002sin(2ωt)，其中 ω 为系统的激励圆频率(ω=2π500/60)。系统中其它参数见表1～表3。

表1 多楔带和单向离合器的参数Tab.1 Parameters of the belt and OWC

表2 SBAD系统中各轮的参数Tab.2 Parameters of the pulleys in the SBADs

表3 张紧器的参数Tab.3 Parameters of the tensioner

2.2 有/无单向离合器装置对系统动态特性影响

有、无单向离合器装置时，SBAD系统旋转振动的动态特性计算值见图3。

由图3(a)可见，SBAD系统中加入单向离合器装置后，张紧臂和从动轮的角度波动幅值均减小，且张紧臂的角度波动幅值减小最明显，由1.65 deg减小到0.24 deg;由图3(b)可见，带段 B1，B2的动态张力波动幅值也明显减小;由图3(c)可见，带－从动轮间的滑移率由0.08 减小到 0.03，减小了 62.5%。因此，SBAD系统中增加单向离合器装置后，能有效地改善系统旋转振动的动态特性，对于控制整个SBAD系统的振动和噪声有积极意义。

2.3 单向离合器参数对系统动态特性的影响

研究单向离合器参数对系统动态特性的影响是单向离合器与SBAD系统匹配设计和系统振动控制的基础。本小节将从单向离合器的弹簧刚度、附件轴与从动轮转动惯量比等方面，研究不同单向离合器参数下，SBAD系统张紧臂的角度波动、单向离合器弹簧的扭矩、带段B1的动态张力和带－从动轮间的滑移率的变化，从而为单向离合器参数的优化设计提供参考。

图3 有、无单向离合器装置对SBAD系统动态特性的影响(注:‘A’表示有单向离合器装置;‘B’表示无单向离合器装置)Fig.3 Comparison of the dynamic characteristics for the SBADs with or without an OWC

2.3.1 单向离合器弹簧刚度的影响

单向离合器弹簧刚度不同时，SBAD系统旋转振动的动态特性的计算值见图4。由图4可见，随着单向离合器弹簧刚度的增加，系统的动态响应均先减小后增大。由图4(b)、4(d)可看出，单向离合器弹簧刚度较小或较大时，带段B1的张力波动幅值、带－从动轮间的滑移率均较大。这将降低轮轴的使用寿命和加剧带的磨损。

另外，由图4(c)可见，单向离合器弹簧刚度较小或较大时，离合器均处在结合、分离交替的状态，系统的非线性振动较明显;单向离合器弹簧刚度较小时，弹簧扭矩幅值较大，说明单向离合器弹簧的转角幅值也较大，这容易引起单向离合器弹簧的疲劳失效;而单向离合器弹簧刚度较大时，从动轮与附件轴间通过离合器近似刚性连接，单向离合器没有起到解耦SBAD系统与大惯量转子的作用。因此，合理设计单向离合器弹簧刚度的大小，是单向离合器装置与SBAD系统匹配设计的关键。

2.3.2 单向离合器转动惯量比的影响

单向离合器具有不同转动惯量比时，SBAD系统旋转振动动态特性的计算值见图5。

由图5可见，随着转动惯量比的增加，系统的动态响应先减小后增大。转动惯量比太大时，系统的非线性振动特性非常明显，且图5(a)中张紧臂的角度波动幅值、图5(b)中带段B1的动态张力波动幅值、图5(c)中单向离合器弹簧扭矩幅值都很大。因此，合理设计附件轴惯量的大小，对SBAD系统振动控制和节能方面均有较大实际意义。

3 单向离合器参数优化设计

在图4(b)和图4(c)、图5(b)和图5(c)中，带段B1的动态张力和单向离合器弹簧扭矩随单向离合器弹簧刚度、惯量比的变化趋势均相同。因此，为简化优化过程，本文只选择张紧臂角度波动幅值、单向离合器弹簧扭矩波动幅值、带－从动轮间的滑移率幅值最小为优化目标，对单向离合器弹簧刚度和附件轴转动惯量两个参数进行优化设计。单向离合器参数的优化数学模型为:

优化模型(11)属于多目标下的非线性优化问题，可用Matlab中的fminimax函数求解。优化前后的单向离合器参数见表4。

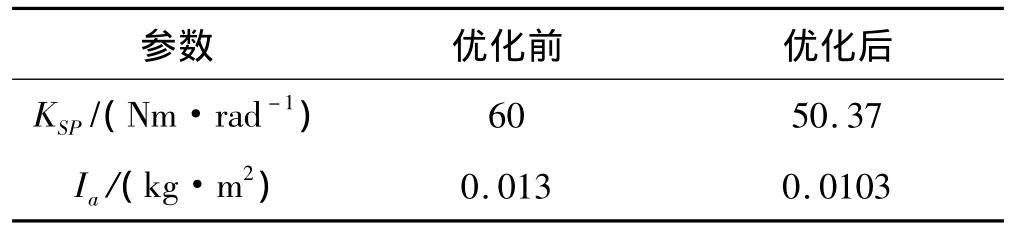
表4 优化前后系统参数对比Tab.4 Comparison of the initial and optimized parameters

SBAD系统优化前后张紧臂的角度波动、单向离合器的弹簧扭矩、带－从动轮间的滑移率随时间的变化关系见图6。

由图6(a)可见，采用优化的单向离合器参数后，张紧臂的角度波动幅值由0.185deg降为0.155deg，降低了16.2%;图6(b)中，单向离合器弹簧扭矩波动幅值由1.40 降为 1.17，降低了 16.4%;图 6(c)中，带 － 从动轮间的滑移率幅值由0.035降为0.029，降低了17.1%。因此，采用优化后的单向离合器参数，SBAD系统的旋转振动动态响应得到了较大的改善，从而有利于控制SBAD系统的振动和噪声。

图6 优化前后系统的动态特性对比Fig.6 Comparison of the dynamic characteristics with the initial and optimized parameters

4 结论

(1)建立了有单向离合器装置的三轮－多楔带SBAD系统非线性旋转振动模型，采用 Matlab中的Gear数值微分算法计算系统的动态响应。SBAD系统中增加单向离合器装置后，系统的动态特性均明显改善;单向离合器弹簧刚度和惯量比过小或过大时，SBAD系统中各元件均表现出较强的非线性振动特性，且动态响应较大。

(2)建立了单向离合器弹簧刚度和附件轴转动惯量的优化设计数学模型，优化结果表明，参数优化后的SBAD系统中，张紧臂的角度波动幅值降低了16.2%;单向离合器弹簧扭矩波动幅值降低了16.4%;带－从动轮间的滑移率幅值降低了17.1%。

由于目前国内单向离合器在附件驱动系统中的应用较少，实验力量较薄弱，本文中的理论计算结果尚待实验验证，需深入研究以完善理论模型。文中单向离合器装置三轮－多楔带传动系统的建模、动态特性求解及参数优化设计的方法，为发动机前端附件驱动系统的旋转振动控制提供了参考。

［1］Hwang S J，Perkins N C，Ulsoy A G，et al.Rotational response and slip prediction of serpentine belt drives systems［J］.ASME Journal of Vibration and Acoustics，1994，116:71－78.

［2］Xu J，Antchak J.New technology to improve the performance of front end accessory drive system［J］.SAE Paper，2004－01－3017.

［3］Zeng X K，Shangguan W B.Experimental investigation on dynamic characteristics of a FEAD system:Affected by serpentine belt length［J］.Applied Mechanics and Materials，2010，34－35:533－537.

［4］Beikmann R S，Perkins N C，Ulsoy A G.Free vibration of serpentine belt drive systems［J］.Journal of Vibration and Acoustics，1996，118(4):406 －413.

［5］韦广梅，王德满，朱应敏.一类刚性常微分方程组初值问题中Gear算法的应用［J］.内蒙古工业大学学报，2000，19(3):166－171.

［6］Zeng X K，Shangguan W B.Experimental and calculation analysis of rotational vibration for an engine front end accessory drive system［J］.SAE paper，2011－01－1534.

［7］KingR， Monahan R. Alternatorpulley with integral overrunning clutch for reduction of belt noise［J］.SAE，1999－01－0643.

［8］Balaji R，Mockensturm E M.Dynamic analysis of a front-end accessory drive with a decoupler/isolator［J］.Int.J.Vehicle Design，2005，39:208 －231.

［9］Zhu F R，Parker R G.Non-linear dynamics of a one-way clutch in belt-pulley systems［J］.Journal of Sound and Vibration，2005，279:285－308.

［10］Leamy M J，Perkins N C.Nonlinear periodic response of engine accessory drives with dry friction tensioners［J］.ASME，Journal of Vibration and Acoustics，1998，120:909－916.

［11］Kraver T C，Fan G W，Shah J J.Complex modal analysis of a flat belt pulley system with belt damping and coulombdamped tensioner［J］.Journal of Mechanical Design，1996，118:306－311.

［12］上官文斌，王红云，张 智.多楔带传动系统振动建模及带段横向振动控制的研究［J］.振动工程学报，2009，22(3):250－255.

［13］Meckstroth R J.Accessory drive belt/pulley friction test［J］.SAE Paper，1998，980837.