基于FEM 和TMM 方法的轨道-隧道-土层振动耦合响应分析
2012-09-15谢雄耀
周 彪,谢雄耀
(1.同济大学 岩土及地下工程教育部重点实验室,上海 200092;2.同济大学 土木工程学院地下工程系,上海 200092)
随着地铁等轨道交通建设的迅速发展,由地铁运营引起的结构及环境响应问题中,比较关注荷载在结构及周围土层中的传播及由此产生的过大沉降及结构损害[1]。
上述问题的研究及解决均须借助于相关的模型。Cui[2]和 Li[3]运用 FEM 对整体式道床和浮置道床轨道结构进行模拟,前者对两种轨道结构的响应差别做了研究,后者对不同结构形式的浮置道床(短、中、长道床)在简谐荷载作用后荷载传递差异做了研究。并讨论了各种模型的使用条件。上述仅对隧道结构进行模拟,而未将隧道及土体进行耦合分析。Takamiya[4-5]针对地表路堤系统将轨道系统和半无限体土层耦合。后续圣小珍[6-7]建立了轨道-多土层模型,研究简谐荷载和半静定移动荷载作用下土层的响应与荷载传递,其中土层运用了TMM法。上述模型并未考虑隧道结构的影响。
随着轨道交通相应的振动问题日益受到关注,很多研究者对隧道结构的影响进行研究,同时之前路堤结构的相关研究也为此做出了积淀。其中Metrikine[8]建立了二维理论模型,将隧道简化成欧拉梁并将其与上下土层耦合,研究了静定和简谐荷载作用下地表位移响应的差异。而该模型未包含轨道结构的影响。Hussein[9]结合PIP模型研究了简谐荷载作用下轨道-隧道-土层结构的响应问题,而该模型仅是针对深埋隧道的特例。
除上述理论模型,有限元及边界元等技术被用于振动传播与响应的模拟,Gupta[10]等将2.5维技术以及FE-BE耦合结构做出模拟;杨永斌[11]将2.5维技术与有限元及无限元技术集合探讨了地下隧道中振动波的传播,刘卫丰等[12],边学成等[13]也就此类方法做了研究,此类模型能较好的模拟结构与土层耦合状态下的响应问题,但计算较为复杂。
为此本文结合上述研究成果,分别利用FEM和TMM方法将轨道结构、隧道和土层进行耦合。并以上海四号线为例,结合耦合结构频散特征,对轨道及土体响应特征作出分析。
1 模型介绍
如图1所示,轨道系统与隧道相连并埋在土层中。轨道系统采用有限元(FEM)进行模拟,振动波在上下土层中的传播则通过传递矩阵(TMM方法)进行模拟。作用于轨道系统上的列车荷载简化为沿铁轨方向上以速度c移动的半静定和简谐移动荷载。
对速度c沿x方向运动的简谐荷载,可表示为:P0eiΩtδ(x -ct),δ为 Dirac's delta 函数,经傅里叶变换后,在f-k空间(频域-波数域)中的表达式为:
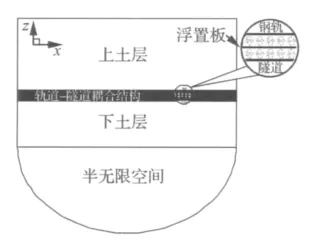
图1 模型概要图Fig.1 The layout of the model
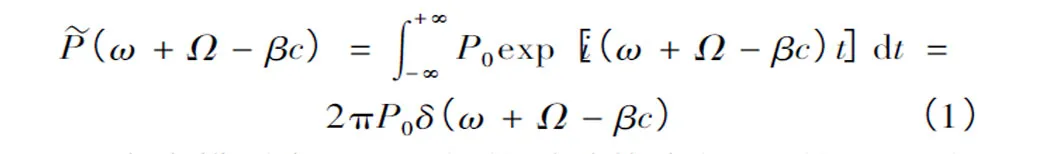
在本模型中以浮置板轨道结构为例,钢轨,浮置板及隧道简化为欧拉伯努利梁并假设无横向运动,其在f-k域中的运动参量表示为:
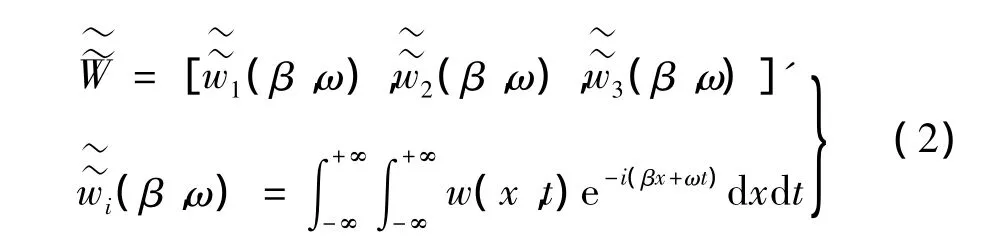
深度方向z=z0上土层的位移与应力表示为:
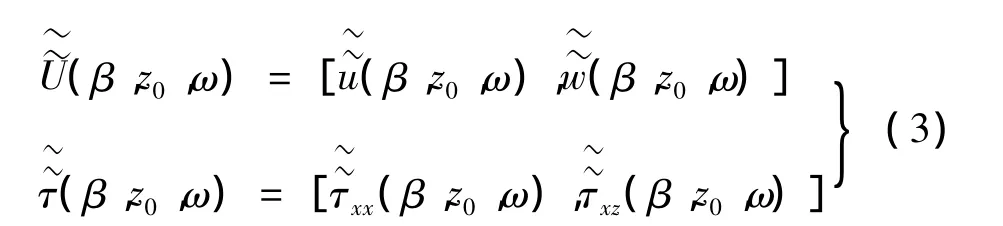
在式(1)所示移动荷载作用下,基于傅里叶与拉普拉斯变换原理并令ξ=Ω-βc。时间空间域内轨道、隧道及土层位移表示为式(4)形式:在列车运行初始时刻(t=0),此式演变为式(5),此为标准的一维傅里叶逆变换。假如已知(β,z0,ω),(β,z0,ω)的值,则在空间域中轨道、隧道及土层的应力与位移便可求得。+∞
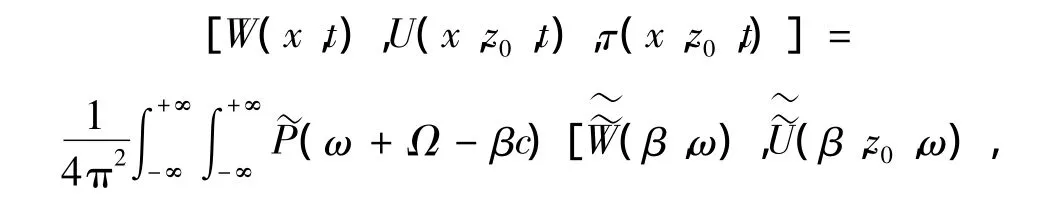
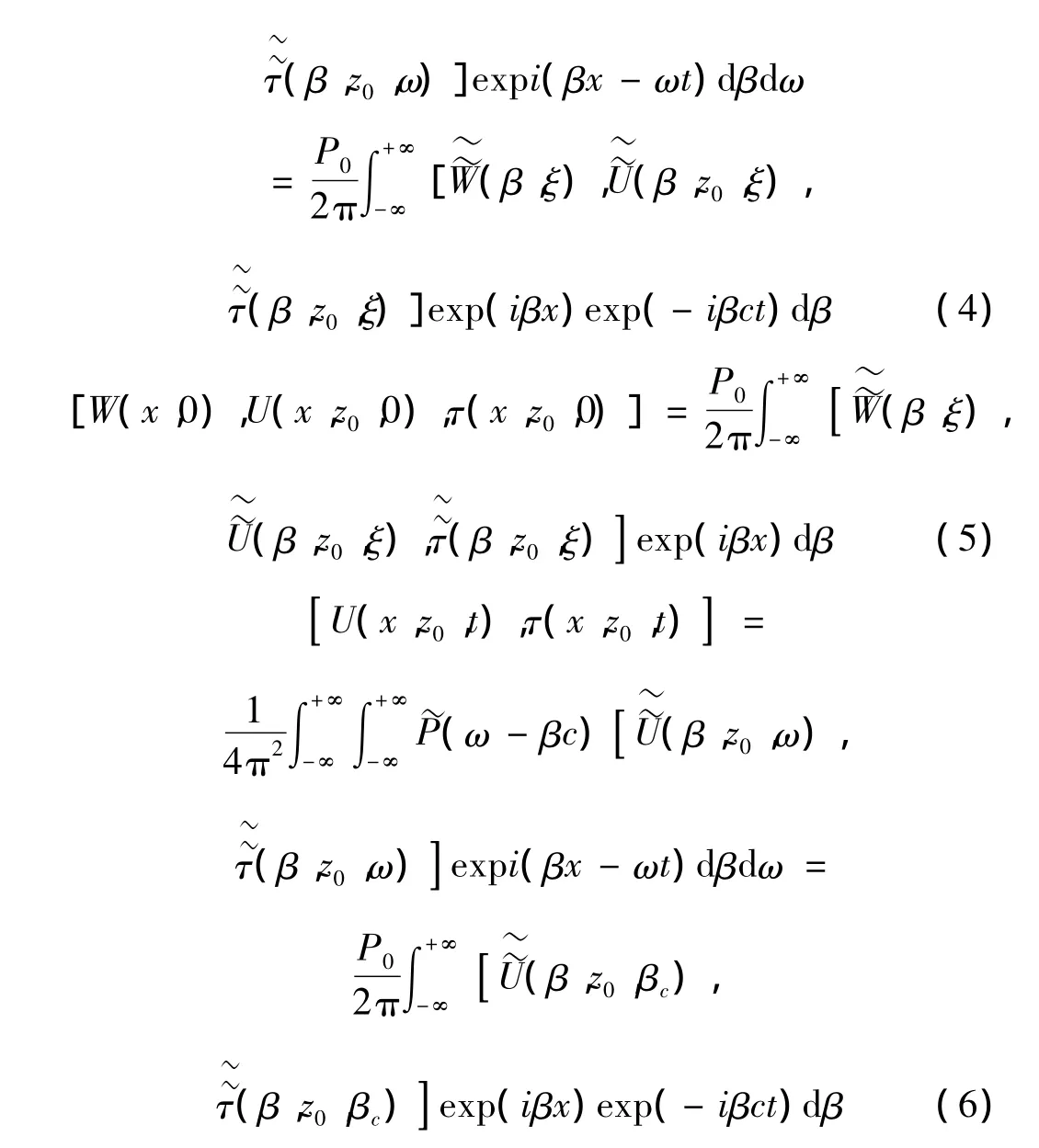
以同样方法,可求得在移动静定荷载作用下时间空间域中的轨道、隧道及土层响应式,即式(6)。
Ω=0时,式(4)即等价于式(6),从某种意义上说,静定荷载仅为移动荷载的特例。故在后续推导过程中仅考虑移动简谐荷载的情况。
2 轨道系统有限元模拟
如前所述,轨道结构及隧道的模拟将采用有限元方法,针对浮置板轨道结构,根据文献[2],浮置板轨道结构可分长、中、短浮置板三种形式,现浇结构宜视为长浮置板形式,可将其简化为梁。另外其与同样简化为欧拉梁的钢轨和隧道之间的扣件及弹性支撑连接简化为弹簧。其弹性刚度分别用kp和kpe表示。在不考虑横向位移的前提下,各部分平衡方程可表示为:?
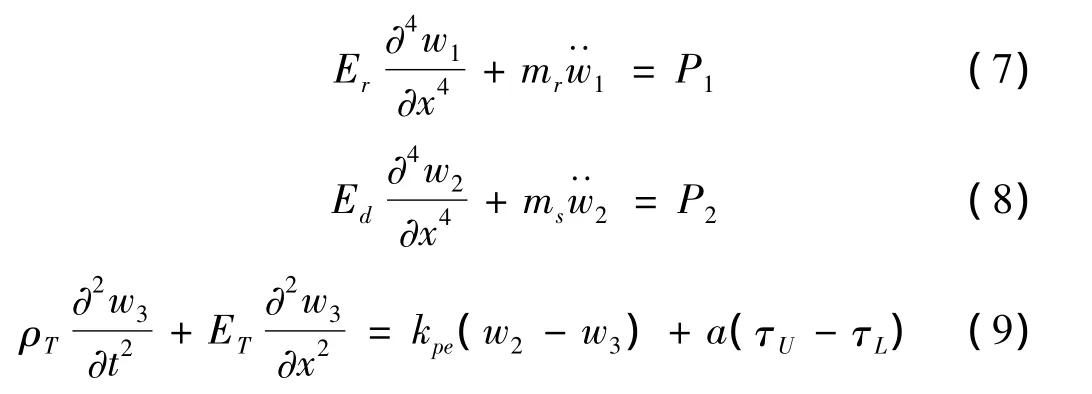
其中:w1,w2和w3分别为轨道,浮置板及隧道的竖向位移,Er,Ed和ET为轨道、浮置板及隧道的抗弯刚度。ρT为隧道每延米质量,τU,τL分别为隧道上下侧土体界面处的应力。
当该耦合结构受到如P0eiΩtδ(x-ct)移动荷载时,分别对上三式就时间t和圆频率ξ进行积分。即可转化为在频率波数域内的一维有限元问题,其刚度与荷载矩阵分别为:
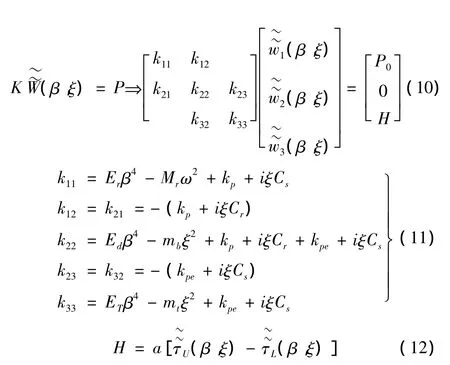
3 傅里叶传递矩阵模拟土层响应
3.1 土层上下界面传递关系
基于粘弹性理论,对于特定土层,其运动方程可以表示为[14]:
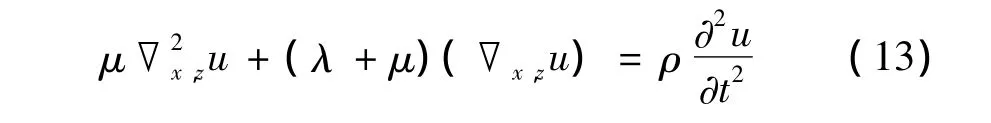
其中:u={u(x,z,t),w(x,z,t)}为距离土层顶部深度 z处的横向与竖向运动分量,ρ为土层密度,λ和μ为粘弹性拉梅常数。其表达式为:
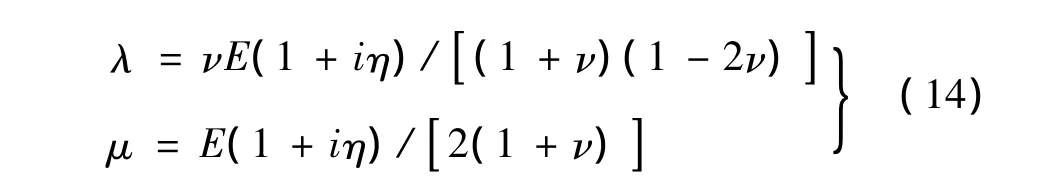
通过对式(14)进行傅里叶变换并求解偏导方程,在土层深度为z处的运动方程表示为:
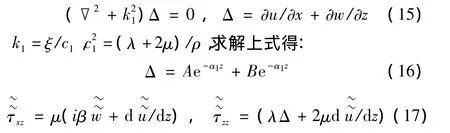
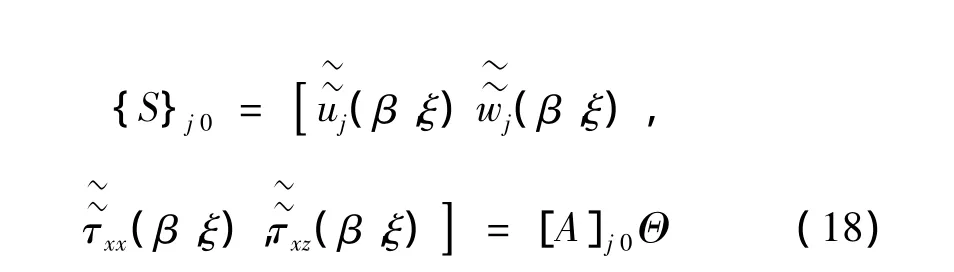
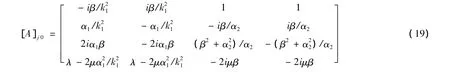
同样方法可获得下表面处应力应变统一表达式:
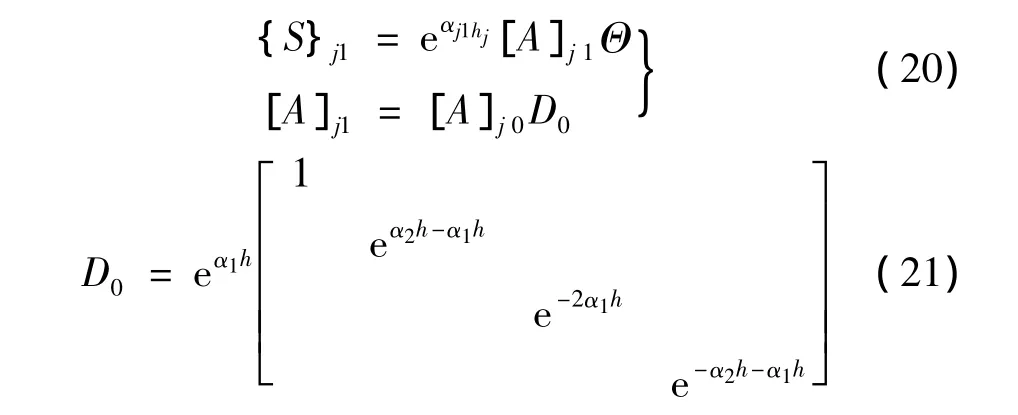
由此,根据式(20)和式(21),土层上下层应力应变可表示为:
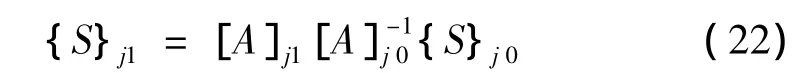
3.2 层状土层整体传递矩阵
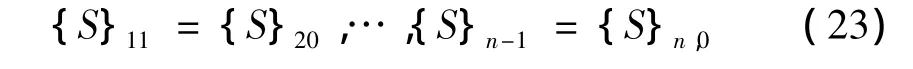
根据Haskell等[14]提出的土层应力应变连续条件:结合式(20),对含有n层的土体,其上表面和下地面的应力应变关系可表示为:
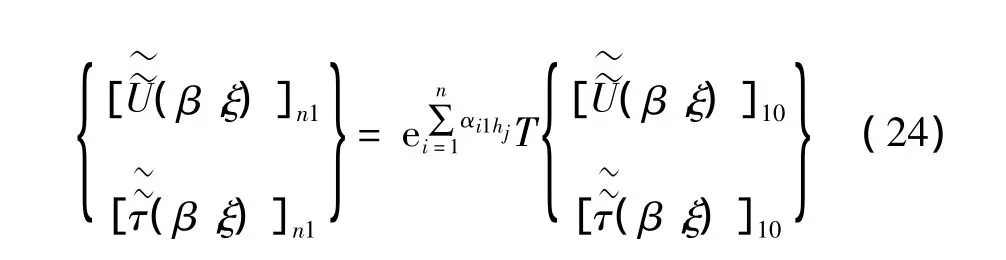
其中:
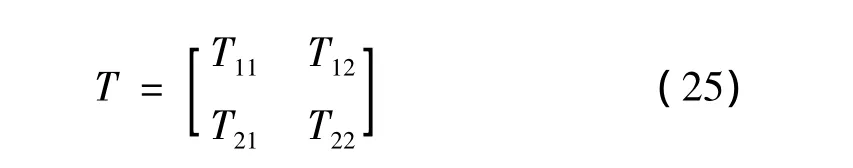
3.3 本模型上下侧土层应力应变关系
如图1所示,隧道结轨道上下侧均为多土层,结合其边界条件,其上下界面应力应变关系为:
(1)上侧土层
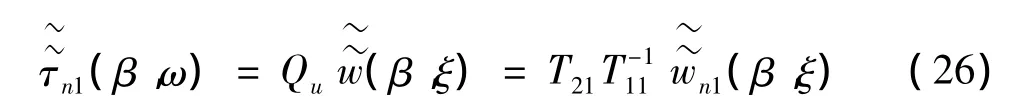
由于上侧土层下表面与隧道梁相连,因而其横向位移为零且其下表面竖向应变量等同于隧道梁,由此接触面上应力应变的关系为:
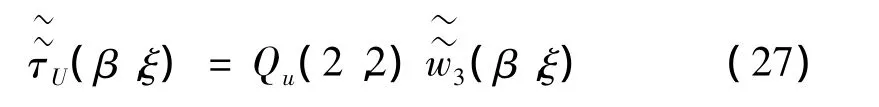
(2)下界面
隧道下侧土层为一多土层和半无限空间体的耦合结构,其中半无限体上边面和多土层的下表面存在连续关系。针对于半无限空间,假定在无穷远处应力应变为零,半无限体上表面应力应变关系可表示为:
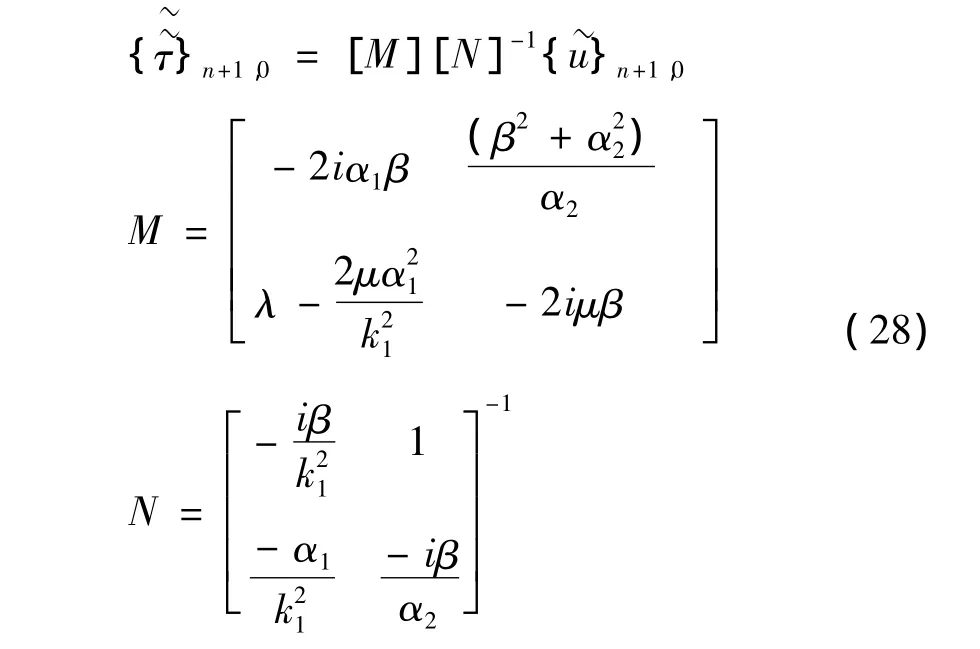
耦合上面多土层,结合式(28),下侧土层与隧道梁耦合的上表面的应力应变关系可表示为:
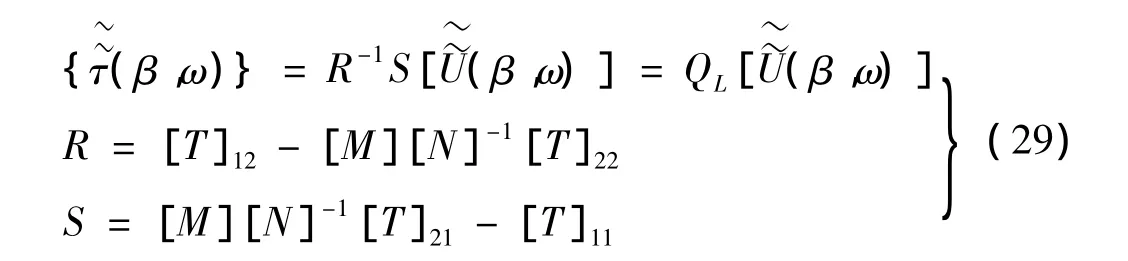
同样,在忽略横向变形的前提下,其竖向应力与应变的关系可表示为:
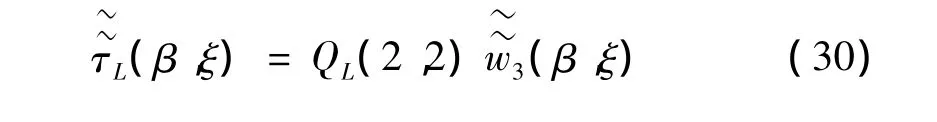
4 实例分析
4.1 研究背景及参数
本文以上海四号线临平-海伦路区间为研究背景,该路段采用浮置板道床,列车具体参数如图2及表1所示:
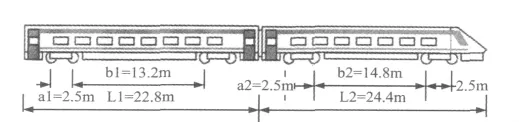
图2 运营车辆几何尺寸图Fig.2 The geometer of operation car at Shanghai metro line 4
为研究方便,隧道上下土层简化为均一土层,其计算参数如表 2所示[15]。
如图2所示的运营列车产生的列车荷载简化为移动速度为60 km/h,幅值为149 kN,其表达式为:
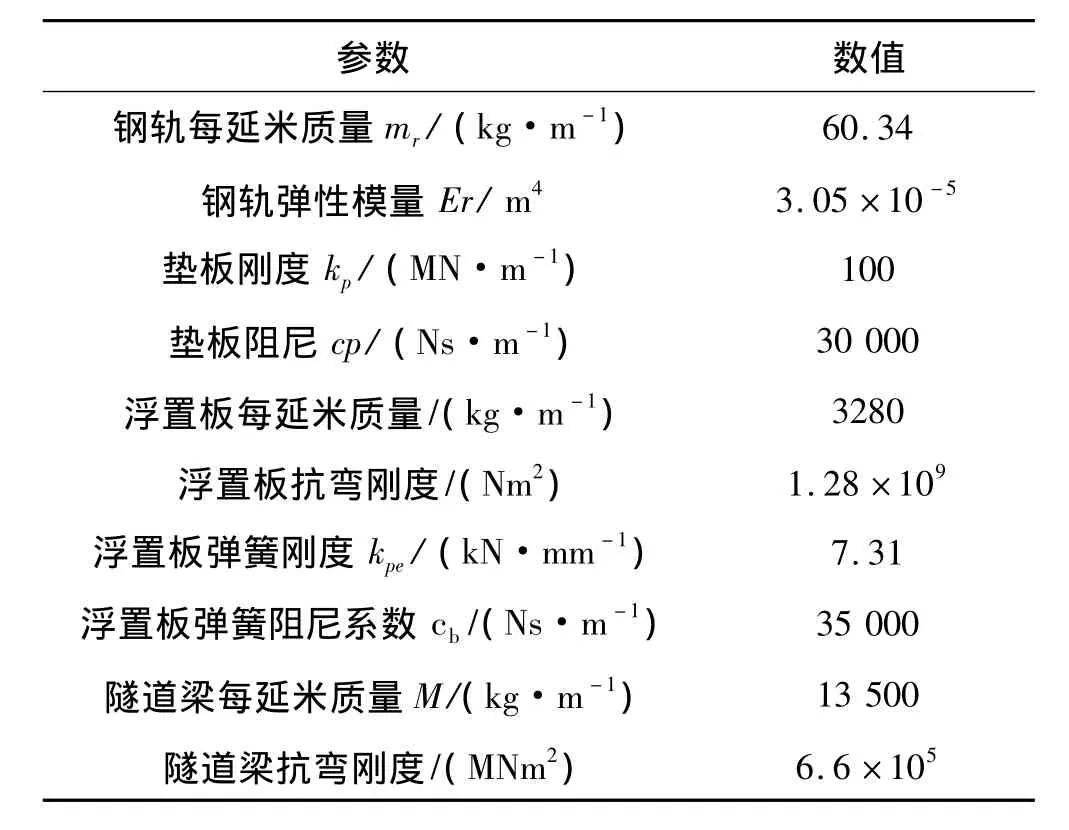
表1 浮置板轨道相关参数(半幅)Tab.1 Parameters of the FST(for half track)
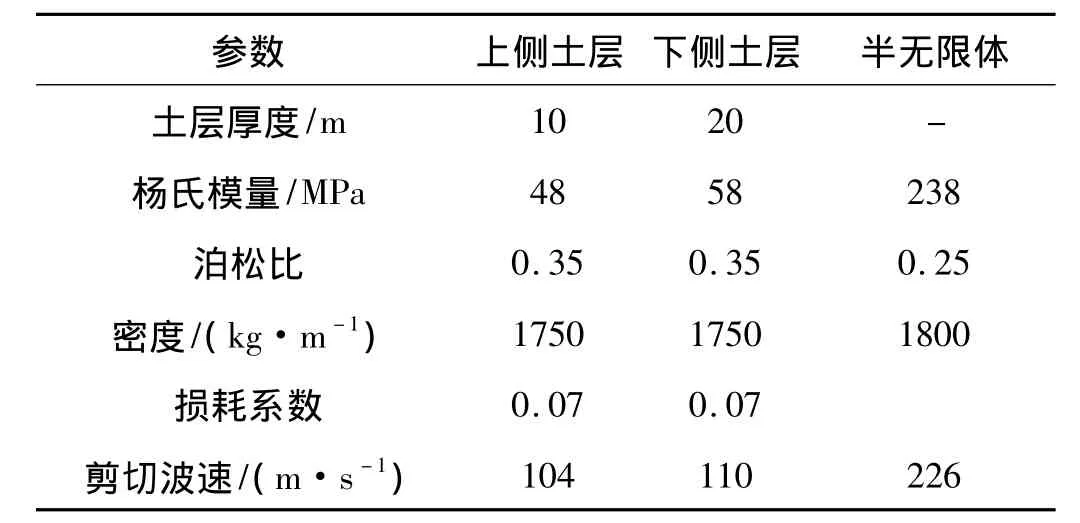
表2 土层参数Tab.2 Parameters for the ground layers

其中:L0为观察点距离第一个荷载的距离,Le为车厢长度。Pn(x-ct+Ln)代表第n节车厢产生的荷载如式(31)所示。其中PNi轮对产生的荷载,其他参数见图2。
对上式做傅里叶变化可得其在f-k域内表达式为:
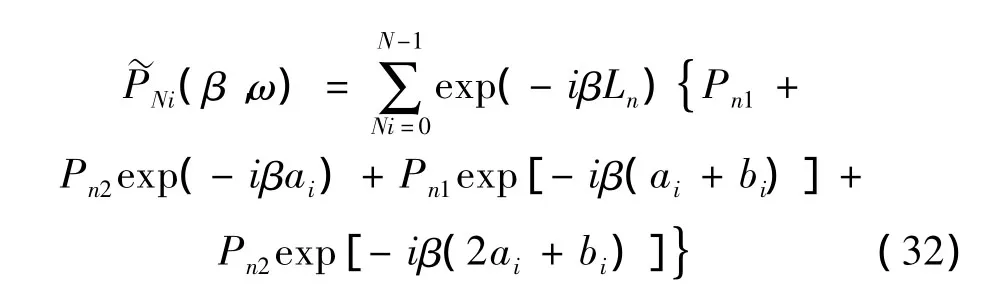
4.2 轨道及土层频散特性分析
为探讨其与土层耦合特征,本节将研究轨道结构和土体频域波数域内频散关系,即分析在无阻尼条件下,响应位移为无穷大时波数β和圆频率ω的关系。
基于式(10),可求得在无阻尼条件下波数和圆频率的关系,其中H是关于β,ω的函数,其值介于0和无穷大之间,所以分析以上H为零和无穷大两者情况,可以从大体上反映轨道结构的频散曲线分布规律,从分析中可以发现在含有隧道梁时,其第一模态区别很小,因而,选定H为无穷大作为计算工况,其频散图如下图3所示。
同样基于式(27)及式(30),并借助MATLAB采用寻找傅里叶极值的方法求取土层在频域内的P-SV频散曲线。其中上侧土层与轨道系统的频散耦合关系见图3。
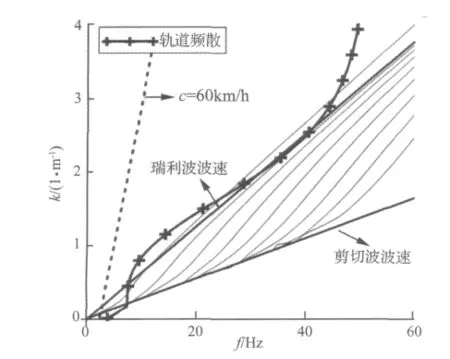
图3 上侧土层与轨道耦合频散特征图Fig.3 The disperse cures of the ground layer and coupled with the track disperse curves
图3中反映了在简谐移动荷载作用下,上侧土层中压缩波和竖向剪切波的频散曲线分布情况。从图中可以看出,除第一模态与瑞利波速曲线相交之外,其余模态均介于土层的瑞利波速和剪切波速曲线范围之内。同时含有隧道梁的轨道系统频散曲线与土层的前两个模态相交。从中可以发现两个重要频散特征。其一就是多普勒效应,对于特定频率来说,当其移动速度超过极限速度时,土层多会产生多普勒效应。以静荷载对上侧土层影响为例,其极限速度可以通过上层土层模态曲线与土层瑞利波速曲线相交点(f0,k0)来判断,当静荷载移动速度超过2πf0/k0时,会发生多普勒效应。另外对特定移动速度情况下,如图3所示的虚线代表时速为60 km/h移动的简谐荷载,其与第一模态起点相交,并与频率轴同时相交于2.4 Hz,说明当时速为60 km/h时,其极限频率为2.4 Hz。超过该频率时,亦会发生多普勒效应。
另外一个重要特征耦合结构的共振频率。以第一个交点为例,交点位于点(7.82 Hz,0.41 m-1),说明频率为7.82 Hz的振动波可同时在轨道系统和土层中传播,此时共振效应将会发生,后续的分析验证上述特点。
4.3 轨道响应及与实测数据对比
根据图2中各参数数值,依据式(10),可计算得到频率波数域内钢轨和浮置板的响应值,如图4所示,频域计算范围选定为[-5,5],从图中可以发现波数k值绝对值大于3后,其幅值已很小,从而保证了做逆傅里叶变换时数值无遗漏。通过运用IFFT变换得到如图5及图6所示时域内的响应值。
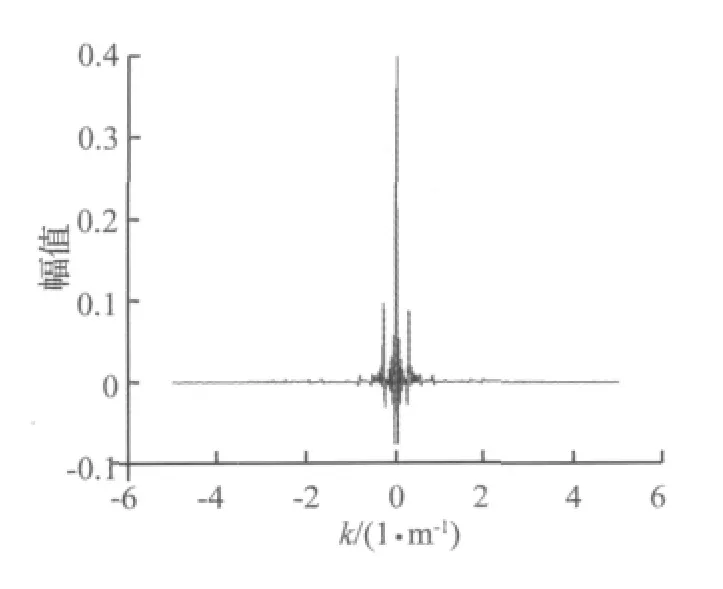
图4 钢轨位移波数域内求解值Fig.4 The rail displacement value at wavenumber domain

图5 轨道位移模拟结果与实测结果对比图Fig.5 The Rail simulation displacement along the x direction and compared with the measures
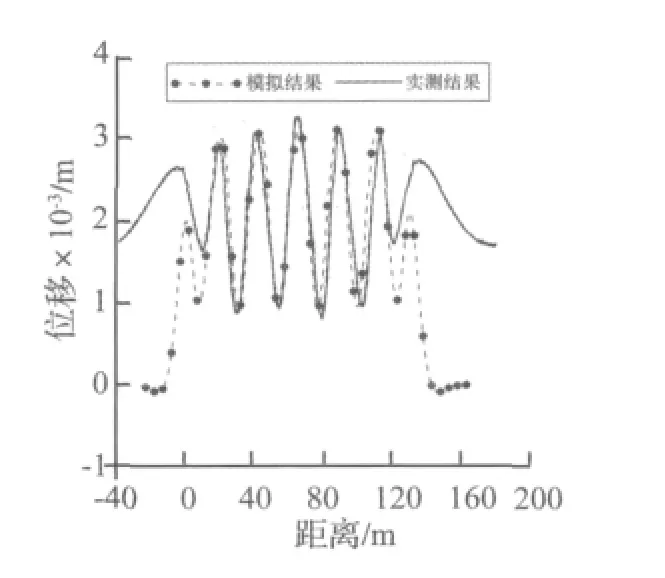
图6 浮置板模拟结果与实测结果对比图Fig.6 The float slab simulation displacement along the x direction and compared with the measures
从图5、图6看出,由于实测数据中包含测试仪器与隧道同振动,因而列车离开时存在小差异,其余部分模拟结果与实测结果吻合良好。说明模型能较好的模拟耦合结构的振动响应。
4.4 地层响应
4.4.1 地表位移
为验证3.3节中频谱分析结论,探讨地表振动随激励频率变化的差异,本文对不同频率下地表位移做了研究。
假设隧道的横向位移为零,竖向位移根据式(10)求解获得的前提下。根据式(20)中Θ值,在土层上下边界应力应变值中的四个值已知,便可求得Θ值,其余四个分量也可同时获得。根据图4频散曲线,分别选取多普勒效应的极限频率下值0.1 Hz和共振频率值8 Hz,一节运营车厢以时速60 km/h经过,分析在上述频率作用下地表位移的区别。

图7 共振与普通激励频率下地表位移图Fig.7 The comparison of the surface displacement under the resonance and normal frequency moving harmonic load
从图7可发现,地表的横向与竖向位移在0.1 Hz频率荷载作用下符合理论解,而8 Hz频率荷载作用发生了多普勒效应。由频散曲线分析得到的与共振频率相近的8 Hz简谐荷载作用下,地表位移值大于其他频率段的响应值。
4.4.2 地层剪力
对于很多岩土工程师来说,或许会更多的关注土层中应力情况,根据4.4.1节中所述方法,同样可以求取不同频率下沿隧道上层土层深度方向的应力值。为分析应力随激振频率的关系,借助本文所述模型计算了不同频率下应力的变化情况。从图8可以发现,在0~20 Hz范围内,应力最大值出现在共振频率附近。与上节中地表位移的分析结果一致。在实际分析与现场测量中,只需获取其中一个物理量的频率分布特征,即可分析振动响应随频率的变化情况。从而为减振措施选取做出参考。
同时本文还选取了8 Hz简谐移动荷载作用下,隧道与上侧土层接触面和地表处沿列车行进方向上的以及x=0处沿土层深度方向上的剪应力变化情况。
从图9发现,剪力也出现明显的多普勒效应。并且在同一频率简谐荷载作用下竖向应力和横向应力的分布形式不同,频率为8 Hz时,竖向应力仍处于第一模态而横向应力出现第二模态,且变化更为复杂。
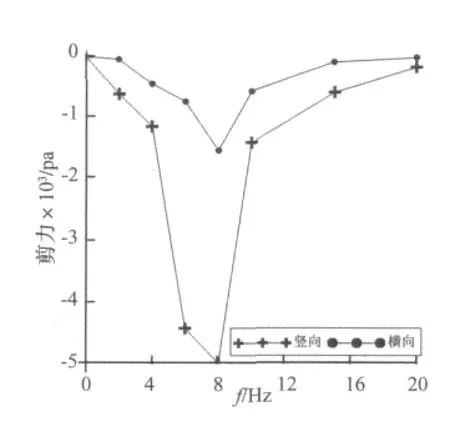
图8 不同频率下上层土层应力最大值分布图Fig.8 The max value of the stress against frequency
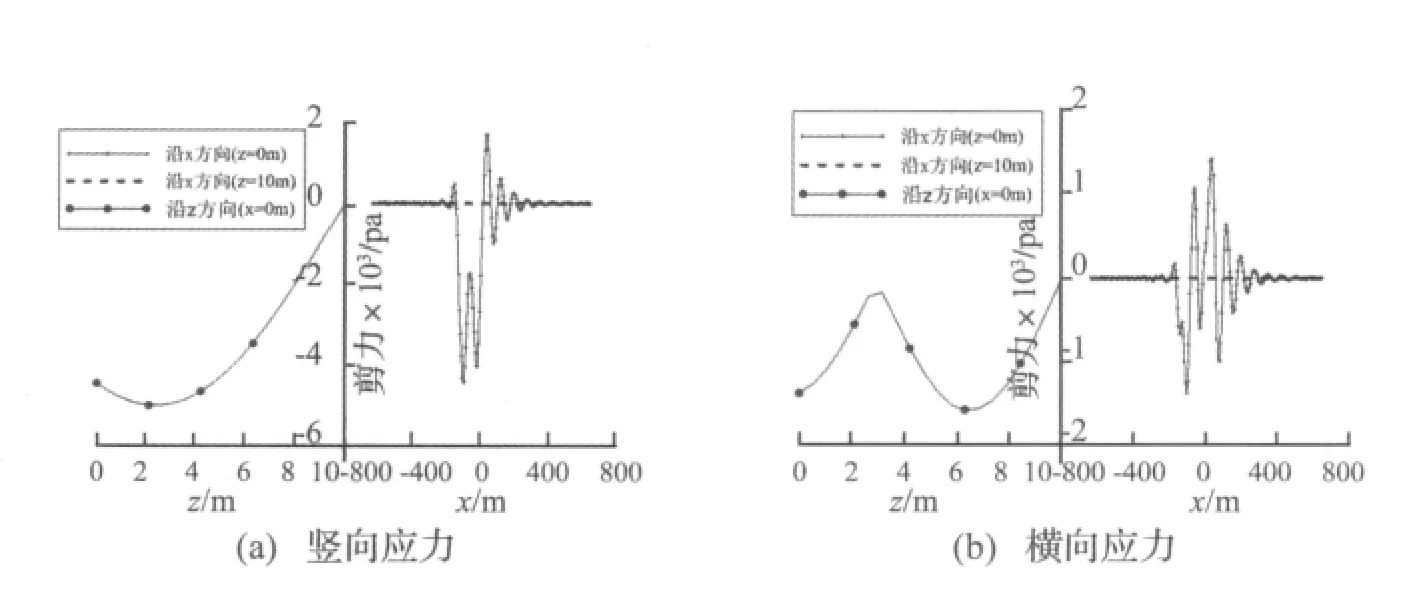
图9 剪力沿列车运行方向及深度方向变化情况Fig9 The stress varies along the train moving direction and depth
5 结论
本文基于FEM原理和TMM方法开发一种用于计算轨道-隧道-土层耦合情况下列车振动引起的振动响应的模型,从与实测结果对比以及相关频散特征分析上看,本模型在研究与计算轨道及土层耦合响应问题上是切实可行的。其能较好的求解轨道系统位移和土体应力应变响应。结论如下:
(1)由轨道隧道系统与土层耦合频散特性分析中,可以清晰得到当简谐移动荷载频率超过一定量值时,将在地表位移及土层剪力中将会出现多普勒效应。
(2)由耦合结构频散特性分析中,从轨道及土层频散曲线的交点(f0,k0)上判断出频率为f0的振动波在波数为k0时,能同时在轨道和土层中传播。如上海四号线轨道与土层共振频率在7.8 Hz附近的激励荷载会造成较大的地表位移与应力。
[1]Li J P,Wang R L,Yan J Y.Research on structural status of operating tunnel of metro in Shanghai and treatment ideas[C].The 6th International Symposium on Geotechnical Aspects of Underground Construction in Soft Ground,2008:315-320.
[2]Cui F,Chew C H.The effectiveness of floating slab track system-Part I.Reacceptance methods[J].Applied Acoustics,2000,61:441 -453.
[3]Li Z G,Wu T X.Modelling and analysis of force transmission in floating-slab track for railways[J].Proceedings of the Institution of Mechanical Engineers,Part F:Journal of Rail and Rapid Transit,2008,222:45 -57.
[4]Grundmann H.The response of a layered half-space to traffic loads moving along its surface,Archive of Applied Mechanics[J].Archive of Applied Mechanics ,1999,69(1):55-67.
[5]Takemiya H.Ground vibrations alongside track induced by high-speed trains:prediction and mitigation[J].Noise and Vibration from High-speed Trains,2001:347 -393.
[6]Sheng X,Jones C J C,Petyt M.Ground vibration generated by a load moving along a railway track[J].Journal of Sound and Vibration,1999,228(1):129-156.
[7]Sheng X,Jones C J C,Thompson D J.A theoretical study on the influence of the track on train-induced ground vibration[J].Journal of Sound and Vibration,2004,272(3 -5):909-936.
[8]Metrikine A V.Surface ground vibration due to a moving train in a tunnel:two-dimensional model[J].Journal of Sound and vibration,2000,234(1):43-66.
[9]Hussein M F M,Hunt H E M.Modelling of floating-slab track with discontinuous slab part 1:response to oscillating moving loads[J].Low Frequency Noise,Vibration and Active Control,2006,25:23 -39.
[10]Gupta S,Degrande G,Lombaert G.Experimental validation of a numerical model for subway induced vibrations[J].Journal of sound and vibration,2009,321(3 -5):786-812.
[11]Yang Y B,Hung H H.Soil vibrations caused by underground moving trains[J]. Journal of Geotechnical and Geoenvironmental Engineering,2008,10:1633-1644.
[12]刘卫丰,刘维宁.地铁振动预测的周期性有限元一边界元耦合模型[J].振动工程学报,2009,22(5):480-485.
[13]边学成,陈云敏,胡 婷.基于2.5维有限元方法模拟高速列车产生的地基振动[J].中国科学,2008,38(5):600-617.
[14]Kolsky H.Stress waves in solids[M].New York:Dover Publications,Inc.,1963.
[15]张亚军.上海地区土动剪切模量比和阻尼比的统计研究[J].世界地震工程,2010,26(2):171-175.
