数字混响器及其改进

姜晓云，李文靖

（山西大同大学物理与电子科学学院，山西大同037009）

数字混响器及其改进

姜晓云，李文靖

（山西大同大学物理与电子科学学院，山西大同037009）

混响时间是衡量音质的重要参量。为了获得最佳混响时间，采用数字混响器对声源信号进行处理是目前经常使用的方法之一。本文对两种混响器模型进行了详细分析，并对其进行了改进。仿真验证了理论的正确性。

混响时间；数字混响器；滤波器

混响是室内常见的一种声音现象。它是室内声源发出的声音在传播过程中被室内各种界面不断反射和积累的结果。室内的声源连续发声，当达到平衡时停止发声，此时室内声源发射出的声能与被吸收的声能相等，这时室内还会有“残留”的声音，这种现象就是混响。

混响时间是指室内声源停止发声后，声能密度衰减60 dB所经历的时间。混响时间是衡量房间音质的重要参数之一，为了达到预期的听音效果就要确保室内具有合适的混响时间，即最佳混响时间。

房间要达到一个最佳的混响时间并不容易，影响混响时间的因素很多，还有许多不确定因素是我们无法控制的。以前人们只能通过改变室内筑材或者通过室内装修来改变室内混响，有它的局限性。现在，随着数字信号处理技术的快速发展，处理器的处理和运算能力不断提高，可以对声源发出的声音信号进行数字化处理从而改善其混响时间。首先对室内声源产生的冲激响应进行测量来确定该房间的混响特性，然后通过某种数字滤波器对原始声音进行处理来达到人们所预期的混响效果，完成这种功能的数字滤波器称为数字混响器。房间的脉冲响应如图1所示。

数字混响器的冲激响应具有很长的长度，原始的声音信号经过数字混响器处理后就会产生一定混响效果，理论上这个数字混响的能产生如图1所示的房间脉冲响应形式。

图1 房间的脉冲响应

从20世纪70年代开始，数字混响器才被人们所熟知，到现在已衍生出了很多种模型，主要包括Moorer混响模型、Schroeder混响模型、梳状滤波器混响模型、全通滤波器混响模型等。其中Schroeder的数字混响模型影响比较大，人们在它的基础上对数字混响模型进行了更进一步的发展。下面我们着重讨论两种数字混响模型对混响的处理。

1 梳状滤波器混响模型

梳状滤波器的内部有一些按一定频率间隔相同排列的通带和阻带，只有在一定频率范围的信号才能通过。由于梳状滤波器形成的特性曲线呈梳状形，于是称其为梳状滤波器。

根据理论上对混响生成的分析，对于后期的混响声，我们可以得出简单的数字混响器模型：

式（1）中，x（n），y（n）为分别为输入输出信号，D为延迟时间，a为衰减系数（a﹤l）。那么该混响器的系统函数为：

用等比数列求和公式可将（2）式变为：

由式（3）可以得到该混响器的系统框图如图2所示。

图2 梳妆滤波器系统框图

在Matlab平台下对其进行仿真，可得到它的频率特性和脉冲响应（取m=8，g=0.5），如图3、图4所示。

图3 梳状滤波器频率特性

从频率特性图3来看，其幅频特性呈明显梳状，这样系统接收到不同频率的信号时就会产生波动情况，出现声染色现象，使声音信号失真，经过处理得到的声音听起来就会很不自然。由图4可见，该脉冲响应幅度随时间呈间断的逐渐递减的情形，实际的混响情形与上面图1所示的走向基本相似，但是可以明显看到与实际极不相符的情况，就是该混响系统产生的声音谱线是平均分布的，且非常稀疏。这意味着它产生的回声密度几乎是不变的且非常低，而且它不会随着时间的延长而加强，这样不能达到我们所期望的混响效果。

图4 梳状滤波器的脉冲响应

2 全通滤波器混响模型

全通滤波器具有平坦的频率响应，它不能衰减任何频率的信号，也就是说它没有滤波作用。虽然它不能改变输入信号的频率特性，但它会改变输入信号的相位。

根据全通滤波器的上述特性人们设计出一种全通滤波器的混响模型来改善梳状滤波器混响模型出现的问题，其系统框图如图5所示。

图5 全通滤波器系统框图

由图5可以看出其改进的方法就是在梳状滤波器混响模型的基础上加了一个反馈支路。图中Z-m表示延时，g（g﹤l）表示反馈增益。图5所示混响模型的系统函数为：

为了更清楚的了解全通滤波器的混响特性，我们在Matlab平台下对该混响模型的频率特性和脉冲响应进行仿真（取m=8，g=0.5）结果如图6、图7所示。

图6 全通滤波器的频率特性

图7 全通滤波器的脉冲响应

由图6所示的频率特性可见，幅度谱呈一水平直线，即使输入不同频率的声音信号也不会有波动的现象，声音信号也不会失真，也就不会出现声染色现象；它的相位谱是呈线性波浪状的，随时间逐渐递减，这样输入的声音信号就会有不同的相位，使声音信号叠加或者抵消，在频谱中产生许多波峰和波谷，从而产生不同的声音，达到预期混响效果。

从图7所示的脉冲响应来看，与梳状滤波器的脉冲响应基本相似，问题仍是系统产生的回声密度不够高，且不会随时间的延长而加强。这样还是不能达到预期的混响效果。

现在我们要解决的问题就明显凸现出来了，由于全通滤波器比梳状滤波器的优势在于能解决声染色现象，每一个滤波器频谱都是全通的，现在如果把几个全通滤波器串联在一起形成一个整体，理论上这个整体的频谱也是全通的，这时各个滤波器产生的回声就能叠加在一起从而使回声密度加大。这样既能保证没有声染色现象发生，又能解决回声密度低的问题。在MATLAB平台下对此改进的滤波器模型进行仿真，结果如图8所示。由于它的频率特性与全通滤波器模型一致，现在只考虑它脉冲响应的变化。

图8 模型改进后的脉冲响应

由图8可以很清楚的看到这种方法得到脉冲响应图与上面的几乎一样，也就是说这样系统模型产生的回声密度还是不够大，与实际混响效果还是相差甚远，为了解决其回声密度低的问题还需要继续分析研究。

在实际房间内人们听到的是混响音效的多次反射波，这些声波随着多次反射而逐渐衰减，从仿真结果可以看到每隔相同的时间脉冲和相位就会递减，也就是说该混响模型产生的声波在房间内每次反射时间间隔相同。如果把几个全通滤波器嵌套在一起，即将图5中的Z-m部分换成一个全通滤波器。为了与实际情况更加贴近，先把三个全通滤波器嵌套在一起，每个滤波器都取不同参数，然后在MATLAB平台下进行仿真，得到它的频谱特性、脉冲响应如图9、图10所示。3个全通滤波器的参数分别取m=8，g= 0.5；m=6，g=0.6；m=8，g=0.8。

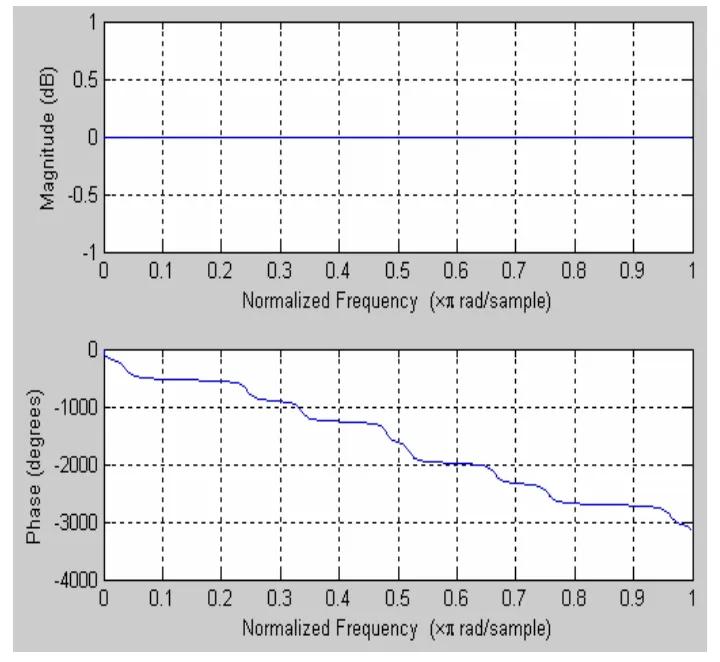
图9 三个全通滤波器嵌套后系统的频率特性

图10 三个全通滤波器嵌套后系统的脉冲响应

由全通滤波器的特性可知，嵌套在一起后形成的新的滤波器模型应该也是全通的，这与图9正好吻合，可见该混响模型系统也不会产生声染色现象。由图10可以明显看到随着时间推移，线条越来越密集，也就是回声密度逐渐变大，这正好符合实际情况，从而解决了回声密度小的问题。这是因为当替换原系统内部的全通滤波器生成回声时，回声就可以通过外部滤波器的反馈环路重新作为输入信号输入，生成的回声数目远比原全通滤波器模型的多，回声密度就会变大，使得信号产生的混响时间变长，听音效果就会显得比较自然了。

3 总结

本文详细分析了两种数字混响模型，它们的模型结构都比较简单，并且容易实现，但都存在着不足，因此对其进行了改进。改进后的混响模型结构一定程度上解决了前者的一些缺陷，但这种结构的缺点是太复杂，不容易实现。所以对数字混响模型必须进一步的进行研究，使其在保证室内听音效果最佳的同时，又能简单方便的运用到实践生活中。

[1]李正周.MATLAB数字信号处理与应用[M].北京：清华大学出版社，2008：89-127.

[2]李承智.人工混响算法[J].电声技术，2002，26（10）：11-13.

[3]周婧洁，陈建平，吉晓东.几种数字混响模型的比较与分析[J].南通大学学报：自然科学版，2010，9（2）：23-28.

[4]王兴国，蒋伟峰.数字混响器设计[J].电子学报，2000，28（7）：84-87.

[5]彭妙颜，张承云.人工混响的设计方法[J].电子技术，2006，30（1）：11-13.

[6]GardnerWG.EfficientConvolutionwithout Input-OutputDelay[J].Journalof theAudio Engineering Society，1995，43：127-136.

〔责任编辑 李海〕

Analysis and I mprovement of the D igital S ound R reverberatol

JIANG Xiao-yun，LIWen-jing
（School of Physics and Electronics Science，Shanxi Datong University，Datong Shanxi，037009）

Reverberation time is the important parameters tomeasure quality.In order to get the optimal reverberation time，adopting digital reverb units to sound signal processing is currently one of the regular use of themethod.In this paper，the two kinds of reverb units on detailed analysismodel，and analyses the improvement.Simulation results prove the validity of the theoretical analysis.

r everberation time；digital sound reverberator；filter

TN713

A

1674-0874（2012）04-0028-04

2012-05-02

山西省自然科学基金资助项目[59637050]

姜晓云（1969-），男，山西大同人，硕士，讲师，研究方向：声信号处理。