三维空间中曲面与曲线的对称

张慧芬，王兰卿

（山西大同大学数学与计算机科学学院，山西大同 037009）

三维空间中曲面与曲线的对称

张慧芬，王兰卿

（山西大同大学数学与计算机科学学院，山西大同 037009）

给出了求曲面和曲线的对称曲面和对称曲线的方法，并举例说明该方法的使用。

曲面；曲线；对称

在高等数学教学中，空间解析几何一章中引入空间直角坐标系后，涉及到了点分别关于点、坐标轴以及坐标平面的对称，这些在课后习题中都有提到，这里不再赘述。但是在空间几何学中关于曲线与曲面的对称曲线和对称曲面的研究，常见特殊情况，本文试着给出几个结论，希望在空间曲线和曲面的对称问题上有所帮助。

1 空间曲面

1.1 关于点对称

定理1空间曲面F（x，y，z）＝0关于定点P0（x0，y0，z0）的对称曲面方程是

F（2x0-x，2y0-y，2z0-z）＝0。

所以

x1＝2x0-x，y1＝2y0-y，z1＝2z0-z。

又点P1（x1，y1，z1）在曲面F（x，y，z）＝0上，有

F（x1，y1，z1）＝0，

故所求对称曲面的方程是

F（2x0-x，2y0-y，2z0-z）＝0。

1.2 关于直线对称

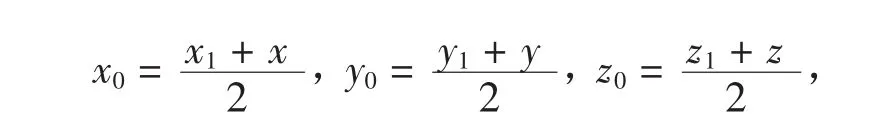
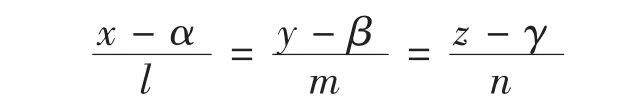
证明 设曲面F（x，y，z）＝0上任一点P1（x1，y1，z1）关于定直线l的对称点是P（x，y，z），且P1P交直线l于P（x，y，z），且P（x，y，z）是—P→P的中点，则：

由（1）（2）整理，化简得

而F（x1，y1，z1）＝0，

故所求对称曲面的方程是

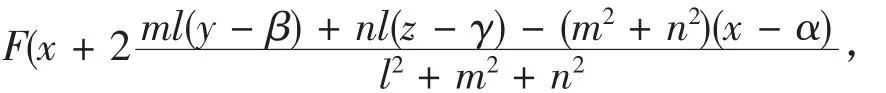
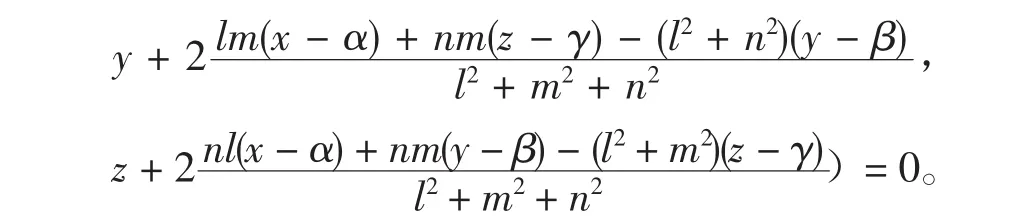
1.3 关于平面对称

定理3空间曲面F（x，y，z）＝0关于平面Ax +By+Cz+D＝0的对称曲面方程是

证明 设曲面F（x，y，z）＝0上任一点P1（x1，y1，z1）关于平面π

Ax+By+Cz+D＝0的对称点是P（x，y，z），且P1P交平面π于P0（x0，

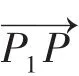
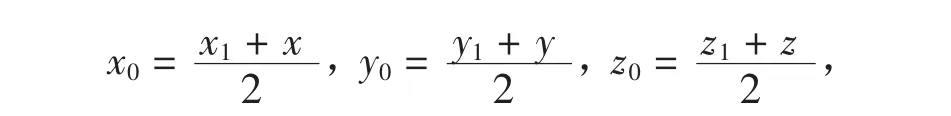
又P0（x0，y0，z0）在平面π上，有

Ax0+By0+Cz0+D＝0

将（4）代入（3），化简得

而F（x1，y1，z1）＝0，

故所求对称曲面的方程是

特殊情形 空间曲面F（x，y，z）＝0关于原点的对称曲面是F（-x，-y，-z）＝0；关于坐标轴x，y，z轴的对称曲面是

F（x，-y，-z）＝0，F（-x，y，-z）＝0，

F（-x，-y，z）＝0；关于坐标平面xoy，yoz，zox的对称曲面是F（x，y，-z）＝0，F（-x，y，z）＝0，F（x，-y，z）＝0。

2 空间曲线

由上述定理1，2，3可类似得到下面结论，不再证明。

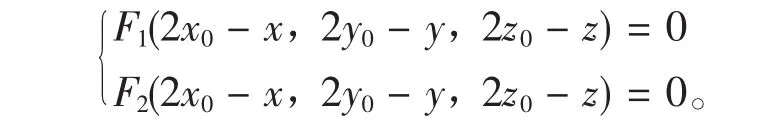
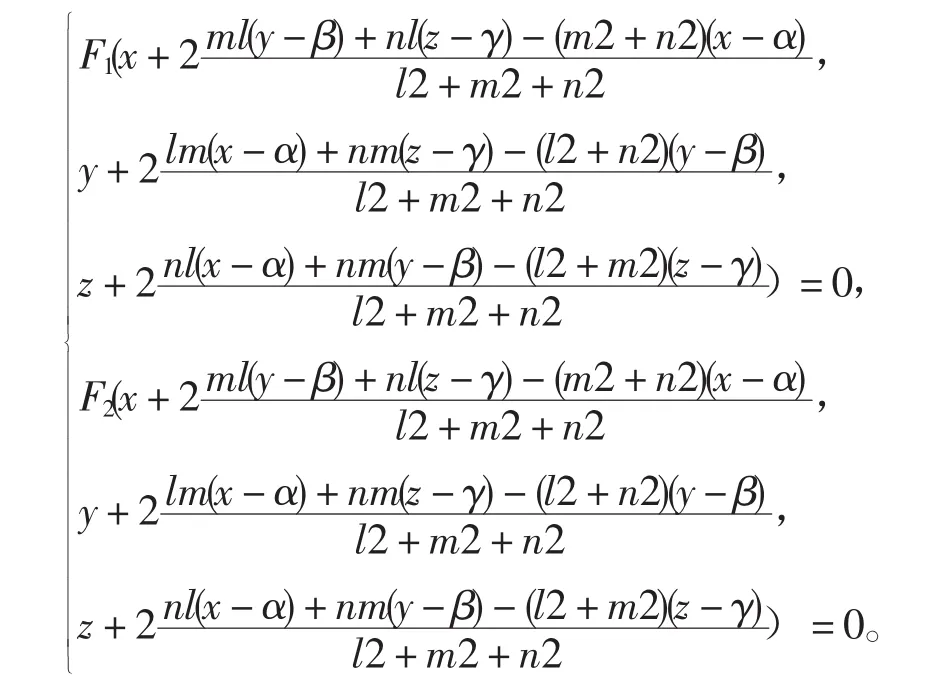
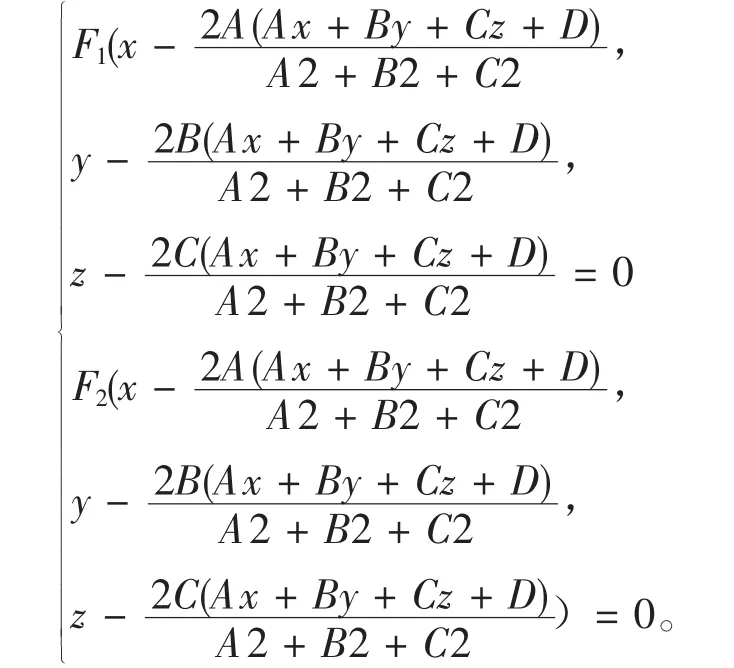
特殊情形 空间曲线 关于坐标轴x，y，z轴的对称曲线是

关于坐标平面xoy，yoz，zox的对称曲线分别是

3 应用举例

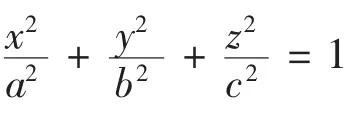
解 由定理1，3可知

所求对称椭球面方程分别是

例1 求椭球面

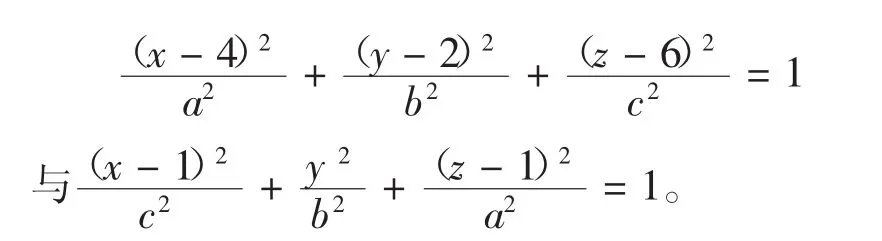
分别关于定点（0，-1，0）与平面x-y+1＝0的对称曲线方程。

解 由定理4、6得对称曲线分别是

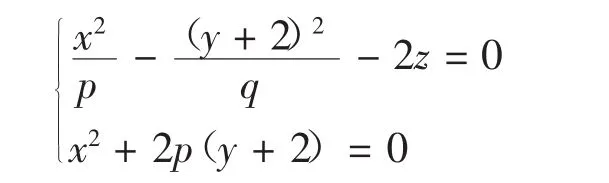
与

[1]吕林根，许子道.解析几何[M].北京：高等教育出版社，2006.

[2]同济大学数学系.高等数学（下册）[M].北京：高等教育出版社，2007.

[3]冯爱萍.曲面与曲线分别关于点、平面的对称曲面和对称曲线[J].科学技术与工程，2007，7（18）：4701-4703.

[4]郑明华.解析几何中有关对称问题的处理[J].数学教学，2006（9）：24-25.

[5]冯爱萍.曲面、曲线关于直线的对称曲面、对称曲线[J].科学技术与工程，2008，8（17）：4961-4963.

[2]方丽箐.空间中关于平面的对称问题[J].广西民族学院学报，2002，8（4）：15-17.

〔责任编辑 高海〕

Symmetry of Curved Surface and Curve in Three-Dimensional Space

ZHANG Hui-fen，WANG Lan-qing
（School ofMathematics and Computer Sciences，ShanxiDatong Universty，Datong Shanxi，037009）

This paper gives themethod to find out symmetrical curved surface，symmetrical curve of curved surface and curve，and then illustrate s the use of themethod.

curved surface；curve；symmetry

O182.2

A

1674-0874（2012）04-0001-03

2012-03-26

张慧芬（1974-），女，山西应县人，硕士，讲师，研究方向：微分方程。