含挠引力的球对称真空解

马孟森

（山西大同大学物理与电子科学学院，山西大同037009）

含挠引力的球对称真空解

马孟森

（山西大同大学物理与电子科学学院，山西大同037009）

用外尔方法计算了爱因斯坦-嘉当理论的球对称真空解。结果表明，在时空几何对称性足够高的情况下，这个方法不仅能用于纯度规引力理论（如：广义相对论）的计算，而且可推广到含挠引力理论中。

挠率；含挠引力；外尔方法

爱因斯坦（Albert Einstein）提出的广义相对论是一个纯度规理论，即只有度规作为动力学变量来描述弯曲时空与物质分布的关系。该理论基于无挠率和度规相容两个条件，联络可以完全由度规来表示，所以此时联络并非独立的动力学变量。广义相对论的真空解有很多，最著名的就是Schwarzschild解，据此可以验证广义相对论在太阳系内的正确性[1]。但是广义相对论并不是一个完善的理论，其本身存在一些不可避免的问题。宇宙大爆炸奇点、黑洞奇点的存在以及构造量子理论的困难都是广义相对论当中存在的大问题。自然地，为了解决或者缓解这些问题，我们要考虑修改广义相对论。

事实上，自从广义相对论横空出世，推广和修改该理论的工作就层出不穷，五花八门。这里我们最关心的是嘉当（E.Cartan）在1922年指出的该理论数学上的一个推广，即考虑不对称的联络 （仿射联络），引入时空挠率。嘉当引入的挠率就是仿射联络的反对称部分。此后，许多物理学家包括爱因斯坦本人都在试图阐述这个推广所包含的物理意义。这也导致之后一系列关于挠率是否存在，能否探测以及如何探测的相关问题的研究[2-8]。从数学上讲，在微分几何中时空挠率和曲率是两个地位相当的量，两者都具有相应的结构方程、Bianchi恒等式。从物理上讲，我们知道所有基本粒子可以根据庞加莱群的不可约幺正表示分类，每种粒子由一组参数（m，s）来表示，前者表示粒子质量，后者表示粒子自旋。质量与庞加莱群的平移部分相联系，自旋与庞加莱群的旋转部分联系。按照Noether定理，物理系统的每个连续对称性都对应某种守恒量。从运动学角度来说，平移不变性给出物质的能动张量，由旋转不变性则得到物质的自旋角动量。物质都是由基本粒子组成的，因此物质的性质应该由基本粒子的性质来刻画。当然，对于宏观物体来说，自旋的贡献相互抵消，导致物质的能动张量起主要贡献。一旦涉及微观物理领域，就需要考虑到物质场的自旋效应的贡献，这时广义相对论变的无能为力。因为广义相对论给出的场方程，左边是描述时空几何的量，而右边只有物质的能动张量。可见，仅从形式上也可以看出爱因斯坦广义相对论仅能用来描述宏观物理现象。研究微观物理现象时，物质场的动力学效应应该是由物质场能动张量和自旋角动量共同决定的。因此，引力场方程左边仅仅考虑时空度规的几何效应已经不够了，时空挠率的几何效应自然需要考虑进来。实际上，有质量的自旋场，如狄拉克场，一定具有不对称的能动张量形式[9]，而爱因斯坦场方程左边是对称的，这也可以从某种程度上表明广义相对论的不完备性。

在引力理论中，研究求解问题最正规的方法是首先由作用量对度规变分得到场方程，再把待定的时空度规带入场方程中，求解所得微分方程（组）即得到具体的时空度规形式。但是这个方法需要求解微分方程，而大部分引力理论的场方程都是很复杂的，所以用此方法求解往往工作量比较大。实际上，赫曼.外尔（H.Weyl）早在1951年在他的著作《space timematter》[10]中就提到可以先把待定的度规带入作用量之中，然后对这个“变形的”的作用量变分，得到简化了的微分方程并求解。尽管能大大简化计算，但是这个方法并非对任何时空、任何理论都可行。1979年，美国数学家R.Palais证明当时空满足某些对称性时（如：球对称、轴对称）外尔方法是成立的[11]。 最近S.Deser把这个方法应用到几种纯度规引力当中得到球对称和轴对称下的真空解[12-13]。

本文中我们先介绍如何用外尔方法求解广义相对论球对称真空解。在第二部分我们给出球对称分布的挠率形式，并用外尔方法讨论爱因斯坦-嘉当理论的球对称真空解。最后在结论中分析所得结果，并讨论外尔方法在求解含挠引力理论的普适性。

1 用外尔方法计算广义相对论真空解

取如下形式的球对称度规

无挠情况下，爱因斯坦-希尔伯特作用量形式为：

由待定度规可得：

式中“′”表示对r的导数，可见括号内后两项均为全微分，其积分结果对最后的场方程没有贡献。

以上作用量对两个独立的度规分量（a，b）分别变分可得：

即

求解可得这就是通常的Schwarzschild时空度规。可见外尔方法在静态球对称时空下应用于广义相对论是可行的，而且相较于常规方法计算过程大大简化了。

2 用外尔方法计算含挠引力理论的真空解

最初的含挠引力理论是爱因斯坦-嘉当理论，该理论具有完全相同的爱因斯坦-希尔伯特作用量形式，区别仅在于此时的标曲率是含挠率的。作用量对度规和联络分别变分，可得到两个独立的场方程：一个是推广的爱因斯坦场方程，另一个是联系物质场自旋流与时空挠率的代数方程。

尽管一般情况下，自旋的引力效应非常微弱，但正如T.Kibble所说，考虑到自旋效应，引力场自身会在一定条件下表现出排斥效应。由于这种排斥效应，在一定条件下就会有避免广义相对论中引力塌缩到奇点以及宇宙大爆炸奇点的可能性。从挠率满足的代数方程可以看出，在爱因斯坦-嘉当理论中，挠率的存在是依赖于物质存在的，没有物质的地方就没有挠率，此时的挠率是非动力学的。因此，不像度规场可以在时空中传播，形成引力波，挠率是不能在真空中传播形成挠率波的。如果挠率真的是以这种理论形式存在的话，那么实验上几乎不可能探测到挠率。因此，人们考虑推广爱因斯坦-嘉当理论及其作用量，并赋予引力以规范场的意义，构造出多种引力规范理论。最主要的有洛伦兹规范引力、庞加莱规范引力和德西特规范引力。除洛伦兹规范引力作用量形式比较简单，其他的规范引力理论都具有复杂的作用量，不仅含有标曲率，还包括曲率平方项和挠率平方项。这种形式的作用量在可重整性和量子化上都更有优势，但显然这种作用量的求解和理论分析也是比较复杂的。因为此时作用量中包含了曲率平方项，挠率不必依赖物质，而是可以独立于物质传播的。

这里我们研究最简单的含挠引力理论-爱因斯坦-嘉当理论[14]，其作用量可记为

其中F表示含挠的曲率标量，其定义与无挠的曲率标量定义类似，只是此时的曲率张量应记为：

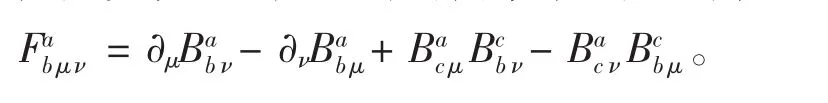
此时我们仍然讨论静态球对称时空，但为了计算方便，线元形式与上一部分略有不同：

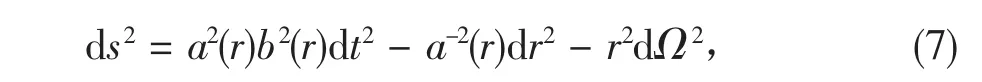
因为此时理论含有挠率，而挠率跟时空度规是独立的，所以还需要单独给定挠率的形式。我们取具有O（3）-球对称的挠率形式：

这里我们采用微分形式语言，挠率可表示为2-形式：

其中

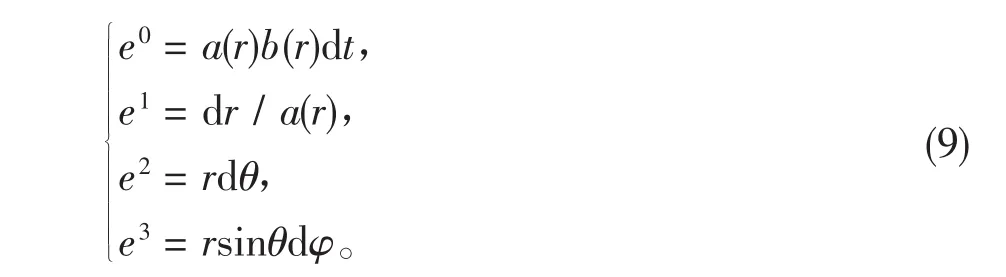
类似的，可算出拉氏密度

对两个独立的度规分量（a，b）以及4个独立的挠率分量（f，h，g，k）分别应用欧拉方程，得到这与常规方法研究所得的爱因斯坦-嘉当理论的结果是一致的，即真空情况下爱因斯坦-嘉当理论与广义相对论是等价的。

用外尔方法还可以研究一种有意思的拉氏量，其中包含挠率平方项：

我们取跟（7）（8）式相同的度规和挠率形式，代入以上作用量，得：

括号中的“…”表示与（10）式中相同的度规导数相关项，这部分的变分方程同样会给出Schwarzschild度规。我们最关心挠率项，对（f，h，g，k）分别变分得到：

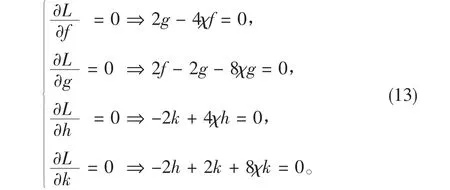
化简结果得：

求解以上两式，只有当χ＝1/4，-1/2时才有自洽的结果，分别对应

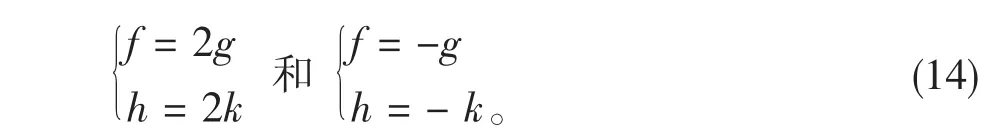
可见，此时我们不能得到挠率的具体结果，只能得到独立分量之间满足的关系，即只要（8）式中给定的挠率满足（14）式的形式，无论挠率取何值，都能给出Schwarzschild度规。

3 结论

尽管许多实验检验表明广义相对论是正确的，但是广义相对论并不是一个完善的理论，其本身还是存在不少问题。不少物理学家考虑引入时空挠率来修改广义相对论。但是含挠理论的场方程一般比较复杂，求解过程更是繁琐。

本文研究了外尔方法求解含挠引力理论真空解问题。结果表明这种方法不仅适用于纯度规引力理论，对含挠引力同样适用，计算过程大大简化。 尽管我们只研究了爱因斯坦-嘉当理论，但是这个方法应该可以用来求解更复杂的含挠引力理论。

[1]Will CM.Theory and experiment in gravitational physics[M].Cambridge Univ.Press，1993.

[2]Hehl FW.How does onemeasure torsion of space-time？[J].Phys Lett A，1971，36：225.

[3]Neville D E.Experimental bounds on the coupling strength of torsion potentials[J].Phys Rev D，1980，21：2075.

[4]Carroll G.Field，Consequences of propagating torsion in connection-dynamic theories of gravity[J].Phys Rev D，1994，50：3867.

[5]Lammerzahl C.Constraints on space-time torsion from Hughes-Drever experiments[J].Phys Lett A，1997，228：223.

[6]Belyaev A S，Shapiro IL.Torsion action and its possible observables[J].Nucl Phys B，1999，543：20.

[7]Belyaev A S，Shapiro IL，do Vale M.Torsion phenomenology at the CERN LHC[J].Phys Rev D，2007，75：034014.

[8]Mao Y，Tegmark M，Guth A，atal.Constraining torsion with gravity probe B[J].Phys Rev D，2007，76：104029.

[9]Hehl FW.On the energy tensor of spinningmassivematter in classical field theory and general relativity[J].Reports on Math Phys，1976，9：55.

[10]Weyl H.Space-time-matter[M].New York：Dover，1951.

[11]Palais R S.The Principle of Symmetric Criticality[J].Comm Math Physics，1979，69：19.

[12]Deser S，Bayram Tekin.Shortcuts to high symmetry solutions in gravitational theories[J].Class Quantum Grav，2003，20：4877.

[13]Deser S，Franklin J，Tekin B.Shortcuts to spherically symmetric solutions：a cautionary note[J].Class Quantum Grav，2004，21：5295.

[14]Hehl FW，Heyde P，Kerlick G D.General relativity with spin and torsion：Foundations and prospects[J].Rev Mod Phys，1976，48：393.

〔责任编辑 李海〕

Spherically Smmetric Vacuum Solutions for Theories of Gravity w ith Torsion

MA Meng-sen
（School of Physical Science and Electronics，ShanxiDatong University，Datong Shanxi，037009）

With the Weylmethod the static，spherically symmetric vacuum solutions are obtained in the general relativity and Einstein-Cartan theory.It is shown that Weylmethod can be employed in any theories with or without torsion on the condition of spacetime with high symmetry.

torsion；theories of gravity with torsion；Weylmethod

O174.5

A

1674-0874（2012）04-0018-04

2012-04-20

山西大同大学博士科研启动项目[2011-B-03]；国家自然科学基金项目[11075098，11175109]

马孟森（1984-），男，河北沧州人，博士，讲师，研究方向：引力理论、黑洞物理、宇宙学。