进化博弈下项目投融资双方均衡结果分析
2012-09-13王静,黄坤,陈瑶
王 静,黄 坤,陈 瑶
(西华大学建筑与土木工程学院,四川成都610039)
我国传统的项目投资融资方式在信息不对称情况下已经暴露出了渠道有限、融资不足等问题。由于工程项目建设周期长、建设耗资巨大,为达到项目预期目标,需要各参与方相互协作、相互信任和相互配合,这增加了项目实施过程的复杂性和难度,相应地会影响资金供给方的投资决心,为了防范金融市场的波动、政策的变化等风险,尽快回收投资及投资所获得的利润,资金供给方加大了监管的力度,压缩资金供给的额度,以提高资金的使用效率;而资金需求方筹集资金的渠道主要是银行信贷,获得银行借款,也因此产生债务负担,资金需求方自筹资金的能力不足,过分依赖金融机构,运用负债筹集资金,也减少了扩大再生产资金的来源。由于资金供给方和资金需求方这种投资融资的方式所带来的弊端日益显现,使得投资方和融资方各自的优势不能最大限度地发挥,双方也不会获得最好的收益。因此,文章利用进化博弈理论,探讨在有限理性条件下投资融资双方的稳定状态。
1 进化博弈在项目投融资中的应用条件
1960年,Lewontin R C,Hamilton W D为了构建他们的研究领域,如动物竞争和动物群中的性别分配以及植物生长等生物进化现象的模型,并借用了经济学家使用的博弈理论中一些基本概念[1、2]。20 世纪 70 年代,Maynard Smith J和Price G R结合生物进化的理论及经典博弈理论,在研究生态进化现象的基础上提出进化稳定策略(ESS)的均衡概念[3]。后来,Gilboa J,Matsui A,Boyland R T等吸收了以上这些研究成果,把生物进化博弈的模型推广到了一般经济行为领域[4、5]。进化博弈理论是现代博弈理论最重要的研究领域之一,被广泛应用于生态学、经济学、心理学和社会学等领域,以研究群体行为的演化过程及其结果,它为经济学的研究提供了一个崭新的分析方法,并且较好地克服了新古典经济学中以及经典博弈理论中的理性假定和多重均衡的困难[6]。
进化博弈理论之中最核心的概念是进化稳定策略(Evolutionary StableStrategy,ESS)和复制动态(Replicator Dynamics,RD)。进化稳定策略表示的是一个种群抵抗变异策略进入的一种稳定状态;复制动态方程表示的是描述一个种群采用某一特定策略的频数或频率的动态微分方程。其表达式分别如下:[4]
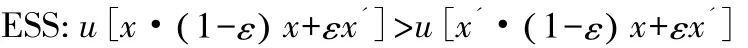

其中:xk为一个种群中采用策略x的比例;u(k,s)为采用策略k时的适应度;u(s,s)为平均适应度。
针对我国项目投资融资方式存在的问题,已有部分学者运用传统经典博弈理论分析项目投资融资双方的行为过程,但由于经典博弈理论是假设博弈局中人为完全理性的,具有对自然的完全信息,并忽略了博弈过程中的学习行为及调整演化,因此对项目投资融资双方博弈过程进行分析存在着一定的不足。而在项目投资和融资的实际过程中,双方均是具有有限理性的主体,他们对事件有一定统计分析的能力,对不同策略效果有事后判断和辨析的能力,但没有预测和预见的能力,对于这种有限理性的群体,可以用进化博弈理论来进行分析。
2 投资方和融资方对一个项目投融资的进化博弈
2.1 博弈条件及收益矩阵
2.1.1 博弈条件
(1)博弈主体:在投融资博弈过程中,文章在该类型下设为投资方和融资方,针对一个确定的项目。
(2)博弈次数:一次性博弈,不进行多次重复博弈。
(3)策略空间:任何一个融资方的选择有融资、不融资,任何一个投资方的选择有投资、不投资,因此,策略空间为(融资,投资),(融资,不投资),(不融资,投资),(不融资,不投资)。
(4)效益函数:融资方选择融资所得收益为R,融资所需成本为C1(R>C1>0);假定C1全部为支付投资方投资所获收益,则投资方投资所得收益为C1;融资方选择不融资,则所得收益为0;投资方选择不投资,则所得收益为0。
(5)概率:设融资方选择“融资”策略的概率为p,选择“不融资”策略的概率为1-p;同时投资方选择“投资”策略的概率为q,选择“不投资”策略的概率为1-q。
2.1.2 收益矩阵
由以上博弈条件可以得出项目投资方和融资方在博弈中的收益矩阵如表1所示。

表1 博弈的收益矩阵
2.2 均衡结果分析
融资方选择“融资”、“不融资”的期望得益U1、U2及融
-资方的平均得益U 分别为:
U1=q(R-C1), U2=0, U
-=pq(R-C1)
投资方选择“投资”、“不投资”的期望得益V1、V2及投
-资方的平均得益V 分别为:

3 投资方和融资方对多个项目投融资的进化博弈
3.1 博弈条件及收益矩阵
3.1.1 博弈条件
(1)博弈主体:在投融资博弈过程中,文章在该类型下设为投资方和融资方,针对多个项目。
(2)博弈次数:一次性博弈,不进行多次重复博弈。
(3)策略空间:(融资,投资),(融资,不投资),(不融资,投资),(不融资,不投资)。
(4)效益函数:投资方选择不投资,则融资方选择融资其他项目,所得收益为R,所需成本为C2(R>C2>0);融资方选择不融资,则投资方只能选择投资其他项目,收益为C3(C3>0);融资方选择不融资,则所得收益为0;投资方选择不投资,则所得收益为0。
3.1.2 收益矩阵
由以上博弈条件可以得出项目投资方和融资方在企业融资博弈中的收益矩阵如表2所示。
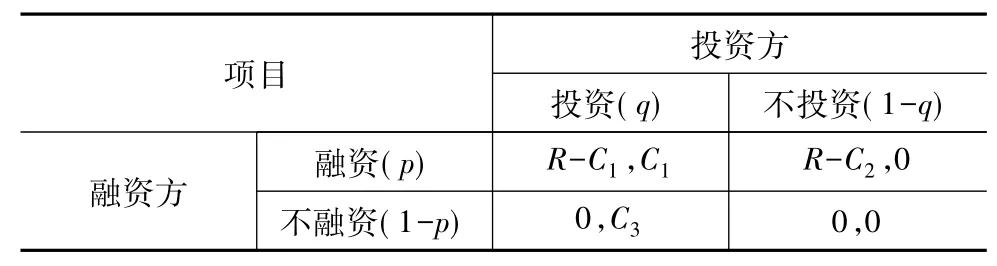
表2 博弈的收益矩阵
3.2 均衡结果分析

4 小结
文章在探讨有限理性条件下投资融资双方稳定状态的过程中,考虑了两个进化博弈理论模型,并通过复制动态方程的稳定点进而得出进化博弈均衡结果,无论投资方和融资方针对一个项目投融资的进化博弈还是针对多个项目投融资的进化博弈,最终进化稳定策略结果均为(融资,投资)。依据前面博弈过程分析可得出,项目融资成功与否与两个因素有关,一是融资所产生的成本(C1或C2),成本越大,被分割的利润(R)也就越大,说明项目融资时,投资方的利润水平对项目有较大影响;二是融资方和投资方选择融资和投资的即时概率(p或q),概率越大,双方所获得的收益相对较好,因此,为了保证概率的可靠性,必须加大融资项目的相关信息的透明度,以此使投资方和融资方发挥各自最大限度的优势,获得双赢甚至多赢。
[1] Lewontin R C.Evolution and the Theory of Games[J],Journal of Theoretical Biology,1961(1):382-403
[2] Hamilton W D.The genetically evolution of social behaviors,I and II[J].Journal of theoretical biology,1964,7(1):17-32
[3] SMITH J M,PRICE G R.The logic of animal conflicts[J].Nature,1973,246:15-18
[4] GILBOA I,MATSUI A.Social stability and equilibrium[J].Econometrica,1991,59(3):859-867
[5] BOYLAND R T.Laws of large numbers for dynamical systems,with randomlymatched individuals[J].Journal of economic theory,1992,57(4):473-504
[6] 何红霞.股票市场中投资者行为的进化博弈分析[J].科技信息,2010(30):148-149
