基于DEM的中国地形起伏度适宜计算尺度研究

张 伟，李爱农

（1.中国科学院水利部成都山地灾害与环境研究所，四川成都610041；2.中国科学院研究生院，北京100039）

基于DEM的中国地形起伏度适宜计算尺度研究

张 伟1，2，李爱农1＊

（1.中国科学院水利部成都山地灾害与环境研究所，四川成都610041；2.中国科学院研究生院，北京100039）

基于SRTM和ASTER DEM数据，在全国范围内选取13个实验区，在渐变尺度下计算平均起伏度变化曲线的“突变点”，据此确定中国地形起伏度的适宜计算尺度；结合山地界定标准计算各实验区山地面积，并采用人工解译的山地范围对计算结果进行检验。研究结果表明：1）地形起伏度适宜计算尺度与所采用的DEM数据有关，DEM分辨率越小，地形起伏度适宜计算尺度越大；2）针对同一分辨率DEM数据，中国境内的地形起伏度适宜计算尺度随地貌特征变化而变化，但总体变化幅度不大；3）针对SRTM和ASTER DEM两种常用数据源，分别选择4.72 km2和3.20 km2作为地形起伏度适宜计算尺度是合理的，山地界定精度达90%以上。

山地；地形起伏度；计算尺度；DEM

地形起伏度亦称相对高度，为“一定范围内海拔的变化”，但“一定范围”具有很大的不确定性和明显的尺度效应，科学认识地形起伏度的计算尺度是基于数字地形模型（DEM）界定山地范围的重要前提［1－4］。《欧洲1∶250万地貌图》采用16 km2作为地形起伏度计算尺度［5］；陈志明等在编制《中国及毗邻地区1∶400万地貌图》时，采用21 km2作为地形起伏度的计算尺度［5］；涂汉明等认为中国存在2 km2、10 km2、16 km2、20 km2、22 km25种计算尺度，而21 km2具有全国普适性，其对应的比例尺为1∶100万［6，7］；郎玲玲等采用1∶25万和1∶10万两种DEM数据，得出适宜计算尺度分别为4.41 km2和0.4 km2［8］。可见，地形起伏度计算尺度并不一致，存在以下争议：对于同一种数据，地形起伏度计算尺度与地形、地貌是否存在关联？地形起伏度计算尺度的选择与DEM数据的分辨率是否有关？本文针对以上问题，分别选择85.6 m和30 m两种分辨率的DEM数据，在全国范围内选取13个不同地貌类型的实验区，通过计算渐变尺度下平均起伏度变化曲线的“突变点”确定地形起伏度计算尺度，并对计算结果进行分析和验证，为我国山地范围界定和山地面积计算提供科学依据。

1 实验区与数据

我国地貌分布的基本规律是西高东低，自西向东形成三大阶梯。第一级阶梯是青藏高原，海拔多在4 000～5 000 m，相对高度为1 500～3 000 m；第二级阶梯是青藏高原的北缘与东缘到大兴安岭、太行山、巫山之间，海拔多在1 000～2 000 m，相对高度为500～1 500 m；第三级阶梯是更东的低山丘陵和大平原，山丘海拔多在千米以下，平原一般不超过200 m，大部分地区的相对高度为200～500 m［9］。根据此地貌特征，本文在全国范围内选取13个大小相同的实验区，每个实验区的面积为5 040 km2（70 km×72 km）。实验区涵盖了各种一级地貌类型，其中，高原实验区涉及青藏高原、黄土高原、云贵高原、蒙古高原，山地实验区涉及新疆山地、重庆山地、长白山，丘陵实验区涉及东南丘陵区，平原实验区涉及成都平原、东部平原、新疆平原和东北平原。本研究采用空间分辨率为85.6 m的SRTM（Shuttle Radar Topography Mission）DEM和30 m的ASTER DEM数据。SRTM数据覆盖了北纬60°～南纬56°之间的所有区域，绝对高程精度为±16 m，绝对平面精度为±20 m［3］；ASTER数据覆盖范围为北纬83°～南纬83°之间的所有陆地区域，绝对高程精度是±20 m，绝对平面精度是±30 m［3］。

2 地形起伏度适宜计算尺度研究

2.1 我国山地界定标准

目前，山地的定义包含定性、定量及介于二者之间3种方式。定量的山地定义便于计算机的自动计算，可以提高山地范围界定的效率和准确性，山地界定标准正是通过完全数字化方式对山地进行定义。在我国，关于地貌类型面积的统计一般将部分丘陵和高原（青藏高原）作为特殊的山地计入山地范围，称之为广义的山地或“大山地”，“我国山地面积占国土面积的2／3以上”正是基于这一原则得出［10－16］。本文也是基于这一原则，并对国际、国内研究结果进行归纳，以地貌分类为目的提出我国山地的界定标准：海拔在500 m以下，相对高度在50 m以上的区域；海拔在500～2 500 m，相对高度在100 m以上或坡度在25°以上的区域；海拔大于2 500 m的所有地区。

2.2 地形起伏度计算

本文采用窗口分析法提取实验区的地形起伏度，计算公式为：

式中：LERi表示以第i个栅格为中心的窗口内的相对高差值，Emax、Emin分别表示该窗口内的最大、最小高程值。窗口分析法的基本原理是：对栅格数据系统中的一个栅格开辟具有固定分析半径的窗口，并在窗口内进行一系列统计计算，窗口在栅格数据矩阵中连续移动完成整个区域的计算。

鉴于朗玲玲采用的数据和本研究采用的数据比例尺相近，得出的适宜尺度为4 km2和0.4 km2［8］，所以本研究在试验中开辟了最大为20 km2的分析窗口。以目标栅格为中心，对SRTM数据分别开辟3×3、5×5、7×7、…、51×51（20 km2）的矩形窗口，对ASTER数据分别开辟3×3、7×7、11×11、…、147×147（19.4 km2）的矩形窗口，通过式（1）求取分析窗口内的高差，作为目标栅格的起伏度值。以DEM上每个栅格作为目标栅格，求得地形起伏度的栅格数字矩阵；对每个栅格的起伏度值求和为S，栅格总数为N，分别求取每个分析窗口内的起伏度平均值M，公式如下：

M值反映出实验区在每个分析窗口下的平均起伏状况，并且以渐变窗口为横坐标、以对应窗口下的起伏度平均值为纵坐标绘制起伏度变化曲线。

2.3 适宜计算尺度确定

现有研究表明，以某一山体上任意一点为地形起伏度的计算中心，随着计算尺度的扩大，相对高差不断增加，起伏度的变化率不断减小，地形起伏度的变化由陡变缓，起伏度变化曲线呈对数曲线［6，7，17］。按照地形起伏度理论及地貌发育理论［6，7，18］，上述曲线必定存在一个高差变化率由大变小（亦即曲线由陡变缓）的点，而且该点是唯一的，地形起伏度的适宜计算尺度就是该“变点”所对应的窗口值。为了更准确地得出该点的值，本研究采用对恰有一个变点的检验最为有效的均值变点分析法［19］求取每个实验区地形起伏度变化曲线的“变点”：设｛Xt，t＝1，2，…，n｝为非线性系统的输出，系统模型或输出序列在某未知时刻突然变化，该时刻即为变点。根据先验知识，地形起伏度变化曲线存在“变点”且唯一，所以“变点”的简单计算步骤为：

（1）将实验区渐变窗口下的平均起伏度值作为均值变点分析法的非线性系统的输出数据，即｛Xt，t＝1，2，…，n｝。令i＝2，…，n，对每个i将样本分为两段：X1，X2，…，Xi－1和Xi，Xi＋1，…，Xn，计算每段样本的算术平均值Xi1、Xi2及统计量Si：

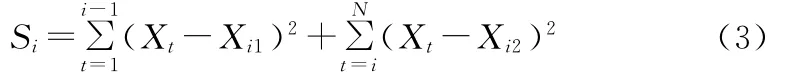
（2）计算统计量X和S：

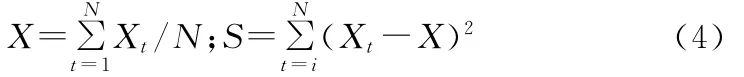
（3）计算S－Si的值Ti，对其进行归一化处理：

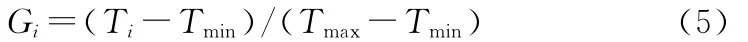
其中：Gi为归一化值，Tmax和Tmin分别为Ti序列中的最大值和最小值。本文建立Gi和地形起伏度渐变窗口之间的对应关系，变点的存在会使Gi增大，即S和Si的最大差值所对应的尺度值即为地形起伏度适宜计算尺度。各个实验区的适宜计算尺度可能不尽相同，本文用离散系数来反映所有实验区的地形起伏度适宜计算尺度的离散程度。统计所有实验区的适宜计算尺度，其离散程度的计算公式如下：

其中：LS为离散系数，SD和AVER分别为所有实验区适宜计算尺度的标准差和算术平均值。离散系数距离零点越远，数据的离散程度越大。

由表1可见，我国境内不同区域的地形起伏度适宜计算尺度略有差异，根据式（6），SRTM数据和ASTER数据实验区适宜计算尺度的离散系数分别为0.168和0.119。SRTM数据的适宜计算尺度介于1.97×1.97～2.48×2.48 km2（3.88～6.16 km2），平均值为4.72 km2；ASTER数据的适宜计算尺度介于1.65×1.65～1.89×1.89 km2（2.72～3.57 km2），平均值为3.20 km2。

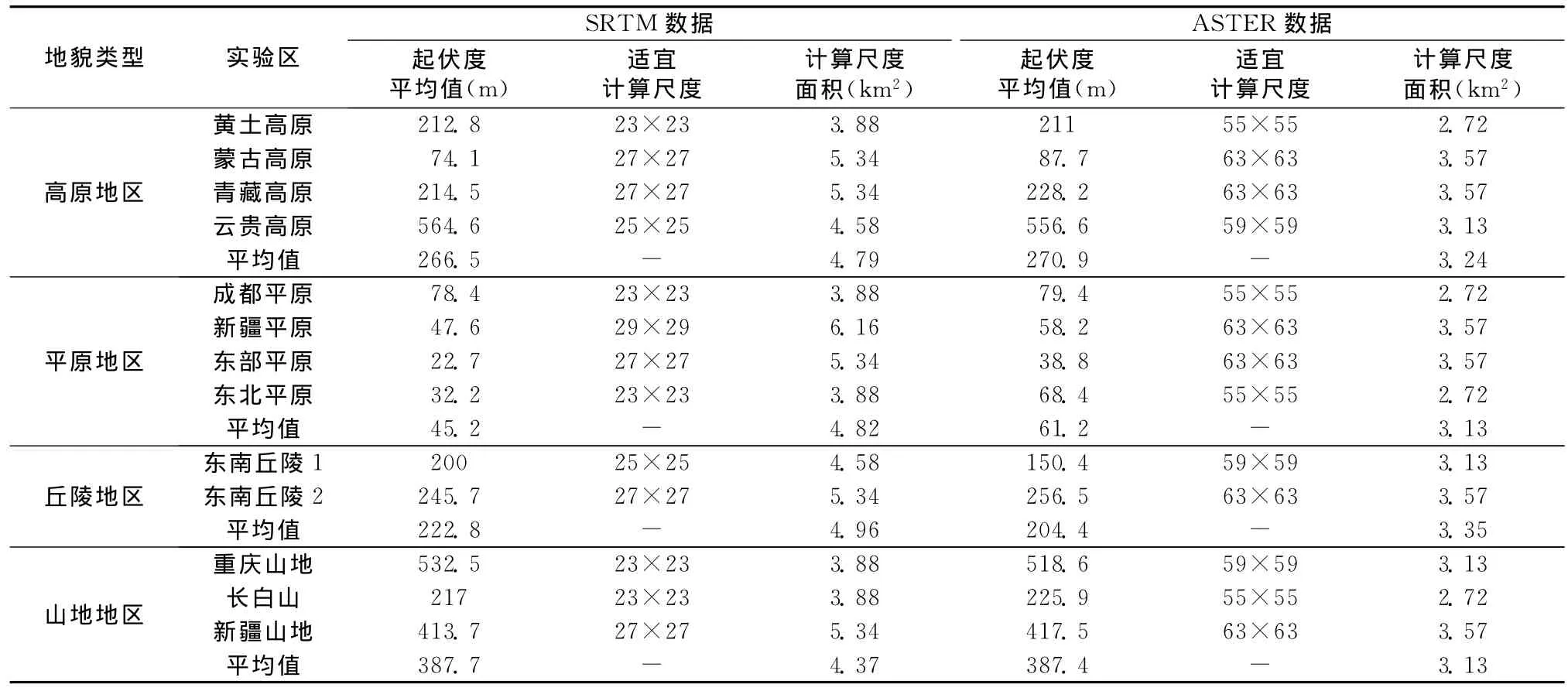
表1 SRTM和ASTER DEM数据实验区“变点”计算结果Table 1 SRTM and ASTER DEM calculation result of experimental area change point

3 适宜计算尺度与DEM尺度及地貌类型的关系

地形起伏度适宜计算尺度的计算结果表明，在相同的区域，如果选用不同的数据源会出现不同的适宜计算尺度。本文采用两种不同比例尺的数据，每个实验区均出现两种地形起伏度计算尺度，而且基于SRTM数据所得的适宜计算尺度均大于基于ASTER数据所得的适宜计算尺度，平均值分别为4.72 km2和3.20 km2（图1）。因此初步认为，DEM数据分辨率越小，选择的地形起伏度适宜计算尺度越大。比例尺为1∶400万、1∶250万、1∶25万、1∶10万的数据分别对应的适宜计算尺度为21 km2、16 km2、4.41 km2和0.4 km2［5－7］。可见，不同比例尺的数据存在不同的适宜计算尺度，比例尺越小，计算尺度越大，本文的研究结果同样证实了这个规律。

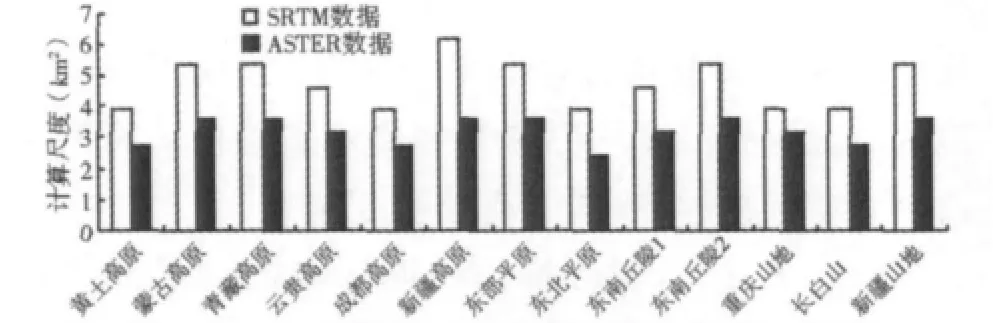
图1 SRTM数据和ASTER数据适宜计算尺度对比Fig.1 The comparison of the optimal calculation scale of SRTM and ASTER data

地形起伏度平均值的计算结果表明，不同的地貌类型具有不同的适宜计算尺度（图2）。根据计算结果将4种地貌类型按地形起伏度从小到大排列为平原、高原、丘陵、山地（表1），其对应的SRTM数据的适宜计算尺度平均值分别为4.83 km2、4.97 km2、 4.79 km2、4.38 km2，ASTER数据的适宜计算尺度平均值分别为3.13 km2、3.35 km2、3.24 km2、3.13 km2。总体上，两种数据的地形起伏度适宜计算尺度与地貌类型呈较为一致的相关。对于同一地貌类型，不同实验区的适宜计算尺度也存在少许差异，这可能与地貌发育的随机性有关［17，18］。

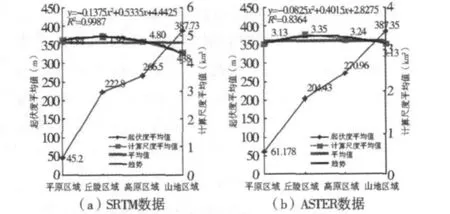
图2 地形起伏度与适宜计算尺度的关联Fig.2 The relation between relief amplitude and the optimal calculation scale for SRTM and ASTER

4 结果验证

对各实验区适宜计算尺度的平均值是否在全国范围内具有普适性进行验证，具体方法如下：在13个实验区中选择3个实验区（黄土高原实验区、新疆山地实验区、东南丘陵实验区），采用本文提出的山地界定标准并结合渐变的计算尺度计算各实验区的山地面积；人工解译出每个实验区的山地范围并得出其面积，将计算结果与解译结果对比并分析绝对误差和相对误差。绝对误差是计算值a与真值A之间差异的绝对值，相对误差R表示为绝对误差与真值的比值（以百分数表示），公式如下：

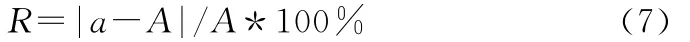
地形起伏度与地貌类型具有一定的关联，但是如果地形起伏度适宜尺度不确定，随地形任意变化，将对区域性乃至全国山地界定带来难以克服的困难。本文所有实验区适宜计算尺度分布较为集中，离散系数很小（分别为0.168和0.119），可以采用样区适宜计算尺度的平均值作为全国尺度上的统一计算尺度，但需要对这个结论进行严格的验证。

分别采用SRTM数据和ASTER数据的地形起伏度计算尺度的平均值4.72 km2（25×25）和3.20 km2（59×59）并结合山地定量界定标准，计算两种不同尺度数据的实验区山地面积。人工解译实验区的山地范围并计算其面积，将计算结果和解译结果叠加（图3），分析计算结果的绝对误差和相对误差。从图3可看出，两种不同的DEM数据源采用各自的平均尺度计算的结果都与人工解译的山地范围比较一致；采用最小窗口（3×3）计算的山地范围远小于解译结果，与实际情况严重不符；采用各自的最大窗口（51×51和147×147）计算的山地范围扩大，将部分非山地计入了山地。可见，针对同一种数据，计算尺度的选择对于界定山地范围有明显的影响，这也反映了适宜计算尺度的选择对山地范围界定的重要性甚至大于所选用的DEM数据源尺度。

图3 新疆山地实验区SRTM和ASTER数据山地面积计算及解译结果Fig.3 The calculation and interpretation result of Xinjiang mountain experimental area based on SRTM and ASTER data

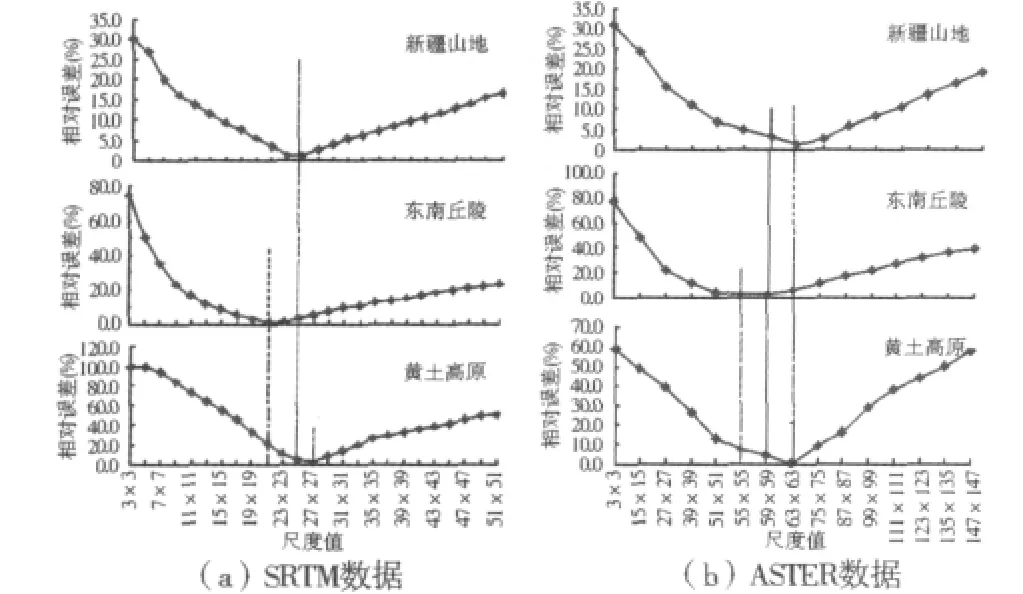
图4 SRTM和ASTER数据山地面积计算结果误差变化Fig.4 Error change of mountain area calculation result based on SRTM and ASTER data

由图4可知，随着计算尺度的增加，山地面积计算结果的误差值呈“U”形变化趋势，说明针对某一实验区存在“最佳”计算尺度。根据这个“最佳”尺度，利用SRTM数据计算新疆山地实验区、东南丘陵实验区、黄土高原实验区的山地范围，与人工解译结果分别相差1.0%、0.5%和2.4%，对应的尺度值分别为25×25、21×21和27×27；利用适宜计算尺度（25×25）估算3个实验区的山地范围与人工解译结果分别相差1.0%、3.4%和4.3%。利用ASTER数据计算新疆山地实验区、东南丘陵实验区、黄土高原实验区的山地范围，与人工解译结果分别相差1.5%、1.5%和0.1%，对应的尺度值分别为63× 63、55×55和63×63；利用适宜计算尺度（59×59）估算3个实验区的山地范围，与人工解译结果分别相差3.2%、2.4%和7.3%。利用适宜计算尺度的计算结果和作为真值的解译结果对比表明，界定山地范围的精度在90%以上。因此，将4.72 km2和3.20 km2分别作为SRTM数据和ASTER数据的地形起伏度统一计算尺度是合理的，且该计算尺度具有全国范围内的普适性。

5 结论与讨论

本文通过实验和分析，得出以下结论：1）地形起伏度计算尺度是山地范围界定和面积计算的重要前提，基于SRTM和ASTER DEM数据，全国范围内的地形起伏度适宜计算尺度分别为4.72 km2和3.20 km2；2）不同尺度的数据源具有不同的地形起伏度适宜计算尺度，DEM尺度越大，地形起伏度适宜计算尺度越大；3）我国境内的地形起伏度适宜计算尺度与地貌类型具有一定的关联，但离散系数很小（分别为0.168和0.119），本文提出的适宜计算尺度适合于全国范围的山地界定。

我国东西地势差异巨大是造成无法统一山地定义的重要原因。赵松乔关于山地的定义［16］：1）有较大的海拔高度，一般在500 m以上，如超过3 000 m一律划为山地；2）有一定的相对高度，如超过500 m即为山地。东部地区相对高程超过500 m的山地很少，按照此定义东部地区基本上“无山”［9］。笔者认为，山地界定标准应该按照我国的特殊地势分段分别进行定义，如海拔在500 m以下的区域、500～2 500 m的区域以及2 500 m以上的区域，这样才能体现我国山地的分布规律，至于在各海拔区间内其他指标以及具体值的设置是否合理，还需要根据具体的应用目的进一步研究。按照本文确定的适宜计算尺度，笔者还估算了我国山地范围，其面积为658.81万km2，与很多文献中“我国山地面积占国土面积2／3”非常接近。

地貌分类的应用目的和所采用的数据源尺度是一切山地界定研究的前提和基础，不同的应用目的对应的山地界定标准不同［14］，相应地也会导致界定的山地范围及面积出现不同。山地地貌形成过程复杂，形态各异，无论是哪种山地界定标准，数据尺度都是不能回避的问题。山地界定标准中所用的相对高度乃至坡度等指标，都反映了尺度的概念，不同尺度的数据源会导致估算结果不同。从这个意义上，本文针对不同尺度数字高程数据源研究全国范围内地形起伏度的适宜计算尺度，是科学界定山地的重要前提。然而，本文仅采用景观尺度的SRTM和ASTER数据，今后需对其他尺度的数据进行相关研究。

中国科学院·水利部成都山地灾害与环境研究所陈国阶先生对本文给予了指导，此致谢忱！

［1］ LIU W，SUN H.Determination of complexity factor and its relationship with accuracy of representation for DEM terrain［J］.Geo－Spatial Information Science，2010，13（4）：249－256.

［2］ PRIMA O D A.Supervised landform classification of Northeast Honshu from DEM－derived thematic maps［J］.Geomorphology，2006，78（3－4）：373－386.

［3］ ZEVENBERGEN L W，THORNE C R.Quantitative analysis of land surface topography［J］.Earth Surface Processes and Landforms，1987，12（1）：47－56.

［4］ 江晓波.中国山地范围界定的初步意见［J］.山地学报，2008（2）：129－136.

［5］ 唐飞，陈曦，程维明.基于DEM的准噶尔盆地及其西北山区地势起伏度研究［J］.干旱区地理，2006（3）：388－392.

［6］ 涂汉明，刘振东.中国地势起伏度适宜统计单元的求证［J］.湖北大学学报（自然科学版），1990（3）：266－271.

［7］ 涂汉明，刘振东.中国地势起伏度研究［J］.测绘学报，1991（4）：311－319.

［8］ 郎玲玲，程维明，朱启疆，等.多尺度DEM提取地势起伏度的对比分析——以福建低山丘陵区为例［J］.地球信息科学，2007（6）：135－136.

［9］ 中国科学院成都山地灾害与环境研究所.山地学概论与中国山地研究［M］.成都：四川科技出版社，2000.

［10］ 钟祥浩，熊尚发.中国山地生态安全屏障保护与建设［J］.山地学报，2008（1）：2－11.

［11］ 钟祥浩，熊尚发.山地环境系统研究新框架［J］.山地学报，2010（4）：385－391.

［12］ 陈国阶.2003中国山区发展报告［M］.北京：商务出版社，2004.

［13］ 程鸿.我国山地资源的开发［J］.山地研究，1983（2）：1－7.

［14］ 丁锡祉，郑远昌.初论山地学［J］.山地研究，1986（3）：179－186.

［15］ 丁锡祉，郑远昌.再论山地学［J］.山地研究，1996（2）：83－88.

［16］ 赵松乔.我国山地环境的自然特点及开发利用［J］.山地研究，1983（3）：1－9.

［17］ 王玲，同小娟.基于变点分析的地形起伏度研究［J］.地理与地理信息科学，2007（6）：65－67.

［18］ 刘新华，杨勤科，汤国安.中国地形起伏度的提取及在水土流失定量评价中的应用［J］.水土保持通报，2001（1）：57－59.

［19］ 项静恬，史久恩.非线性系统中数据处理的统计方法［M］.北京：科学出版社，2000.

Abstract：On the base of SRTM and ASTER DEM data，13 experimental areas across China are selected.Through computing the“change point”of average relief amplitude curve with the gradient scale，the optimal calculation scale of relief amplitude in China is acquired.Based on the previous work，the mountain area of every experimental area can be calculated with mountain definition standard.Then，the calculation results are tested by the way of manual interpretation mountain range.The result show that，firstly，relationship exits between the optimal calculation scale of relief amplitude and DEM data，the DEM data scale greater，the optimal calculation scale of relief amplitude greater；secondly，relationship exits between the optimal calculation scale of relief amplitude and landscape；thirdly，for the SRTM and ASTER DEM，selecting 4.72 km2and 3.20 km2as the optimal calculation scale of relief amplitude is reasonable and testing accuracy is greater than 90%.The study provides a feasible method and reference for calculating the optimal calculation scale of relief amplitude and determining the range of mountain in China.

Key words：mountain；relief amplitude；scale；DEM

Study on the Optimal Scale for Calculating the Relief Amplitude in China Based on DEM

ZHANG Wei1，2，LI Ai－nong1
（1.Institute of Mountain Hazards and Environment，CAS，Chengdu 610041；2.Graduate University of the Chinese Academy of Sciences，Beijing 100039，China）

P208

A

1672－0504（2012）04－0008－05

2012－01－17；

2012－03－15

中国科学院“百人计划”项目（Y1R2130130）；中国科学院知识创新方向性项目（KZCX2－YW－QN313）；中国科学院战略性先导科技专项（XDA05050105）

张伟（1987－），男，硕士研究生，主要从事数字山地与GIS应用研究。＊通讯作者E－mail：ainongli＠imde.ac.cn