一种基于矢量地图特征点和分块的零水印算法

孙鸿睿，朱建军，尹鹏程，施永胜

（1.中南大学地球科学与信息物理学院，湖南长沙410083；2.常德市国土资源规划测绘院，湖南常德415000；3.中国矿业大学环境与测绘学院，江苏徐州221008；4.徐州市国土资源局，江苏徐州221006）

一种基于矢量地图特征点和分块的零水印算法

孙鸿睿1，2，朱建军1，尹鹏程3＊，施永胜2

（1.中南大学地球科学与信息物理学院，湖南长沙410083；2.常德市国土资源规划测绘院，湖南常德415000；3.中国矿业大学环境与测绘学院，江苏徐州221008；4.徐州市国土资源局，江苏徐州221006）

近几年，数字水印作为版权保护的关键技术被用于矢量地图。目前，矢量图形水印算法主要分为空域算法和频域算法［1］，但这两种算法在完成数字水印嵌入的同时，均修改了矢量地图数据，会影响地图精度，而且数字水印容易擦除。针对这一问题，温泉等首先提出了零水印方案，并成功将其应用于数字图像中［2］。零水印是指不修改原始作品的内容，利用原始作品的重要特征构造水印，能解决水印鲁棒性和不可见性之间的矛盾。本文在前人研究的基础上，设计了一种基于矢量地图特征点和分块的零水印算法，可以有效提高数据压缩、顶点增加（删除）以及数据裁剪等操作的鲁棒性。

1 基于矢量地图特征点的零水印构造方案

尽管矢量地图冗余数据相对较少，但在不影响精度的情况下，允许线（面）状数据压缩［3］。为使算法能对抗数据压缩，在水印嵌入前先对原始地图做压缩处理，提取特征点，本文选择矢量数据压缩算法中比较经典的道格拉斯压缩算法；为使地图能对抗裁剪，可对地图进行分块处理，保证每一矩形网格内至少能嵌入一次水印，也可嵌入尽可能多的水印，保证裁剪后图形仍保留完整的水印信息。

1.1 零水印构造方案

可以利用地图分块后每一子块内相邻特征点所在直线的夹角值所对应的二进制序列与置乱后水印图像所对应的二进制序列来构造零水印，本文是对二者进行逻辑运算，实现零水印的构造模式。在地图分块时，为保证每一分块内都能完整地嵌入一次水印，需要预先计算水印信息的比特数；对于给定的水印图像，能够预先知道其水印信息容量，可以据此对地图进行分块。零水印构造流程如图1。

图1 零水印构造流程

1.2 特征点提取

本文选择矢量数据压缩算法中比较经典的道格拉斯压缩算法，其基本思想是［4］：将线划上的第一点作为固定点，最后一点作为浮动点，这两点确定一条直线。计算线划上所有中间点到直线的距离，将距离最大者与事先给定的阈值相比较，如果最大距离小于给定的阈值，则所有中间点均舍去；否则，保留线划上具有最大距离的点，并以此点为基准将整条线划一分为二。重复上述过程，直至没有多余的点可被舍去为止。

1.3 地图分块

假定某一分块内包含相邻特征点所在直线间夹角s个，水印信息比特数为a，因为每个角度值b都可以表示为8位二进制数b′，因此这一分块内能够完整地嵌入一次水印的条件可表示为：8s≥a。依据上述规则，将给定的矢量地图分成n个（可构造零水印的最大数）矩形块。

1.4 水印图像的置乱

为了增强水印的安全性，通常在嵌入水印前对水印进行置乱操作，本文采用Arnold变换［5］，又称“猫脸”变换。对于一幅大小为M＊M的图像，Arnold变换可以表达为：

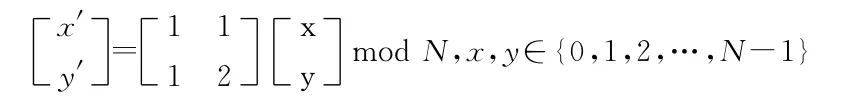
Arnold变换具有周期性，即对图像进行一定次数的Arnold变换后，能够重新得到原始图像。例如，原始水印图像（图2a）尺寸为40＊40，图2b－图2d分别给出了变换1次、10次、30次的置乱结果。当Arnold变换30次后，水印图像将恢复成原始图像，即该图像的置乱周期为30次。

图2 Arnold置乱示例

2 零水印的提取

水印提取为上述水印构造的逆过程，将构造的n个零水印与Li子块内相邻特征点直线夹角所构成的二进制序列Bi′（i＝1，2，…，n；n为分块数）进行二进制按位异或运算，得到置乱后的水印图像，再对该图像进行还原，即可得到n个含有版权信息的原始水印图像。零水印提取流程如图3。

图3 零水印提取流程

3 实验分析

3.1 零水印构造实验

为验证所提算法的可行性和正确性，以1∶500的等高线图为原始地图，以40＊40的水印图像为负载，在Matalab7.0平台上实现本文所提算法。原始地图顶点数为60 251，利用道格拉斯压缩算法提取特征点，本文取阈值0.7，明显高于地图数据所允许的压缩程度，用于提高地图抗简化能力。数据压缩后提取特征点为7 339个，压缩率为88%。

按照上述分块规则对地图进行分块处理，每一分块内至少需要特征点组成角度值40＊40／8＝200个，可将地图分成16块，即可构造16个零水印。

按照上述方法提取出特征点后，计算每一子块内相邻特征点直线夹角Bi（i＝1，2，…，200），并转换成二进制序列Bi′（i＝1，2，…，1 600），与置乱后的水印二进制序列进行按位异或运算，可得到16个零水印。

3.2 零水印的鲁棒性测试

为了检验本文算法的鲁棒性，对矢量数字地图进行平移、旋转、放大（缩小）、顶点删除（增加）及地图裁剪等操作。由于矢量数字地图本身的特性以及本算法采用相邻特征点间直线的夹角构造水印，进行平移、旋转或者缩放均不会影响特征点间直线的夹角，所以前3种操作对水印信息的检测没有影响。

用NC系数作为检测水印与原水印相似性程度的客观度量，对其他攻击的鲁棒性进行测试。水印相似度检验的通用公式为：

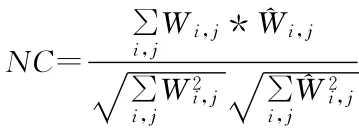
各种处理方式下水印提取效果如表1。

4 结语

本文设计了一种基于矢量地图特征点和分块的零水印算法，利用地图分块后每一子块内相邻特征点所在直线的夹角构成的二进制序列，与置乱后的水印图像进行二进制位异或运算来构造零水印。通过仿真实验分析，该算法可有效对抗地图几何变换（平移、旋转、缩放等），在数据压缩、顶点删除（增加）以及数据裁剪方面具有更强的鲁棒性。需要指出的是，构造的零水印需要送版权注册管理中心（IPR）注册，当版权发生纠纷时，通过公开检测算法提取版权标识才能达到版权保护的目的。

［1］ 闵连权.一种鲁棒的矢量地图数据的数字水印［J］.测绘学报，2008，37（2）：262－267.

［2］ 温泉，孙锬锋，王树勋.零水印的概念与应用［J］.电子学，2003，31（2）：214－216.

［3］ 朱长青，杨成松，李中原.一种抗数据压缩的矢量地图数据数字水印算法［J］.测绘科学技术学报，2006，23（4）：281－283.

［4］ 华一新.地理信息系统原理与技术［M］.郑州：中国人民解放军测绘学院，1999.

［5］ ARNOLD V I，AVEZ A.Ergodic problems of classical mechanics［A］.Mathematical Physics Monograph Series［C］.New York：W A Benjamin，Inc，1968.

2012－02－07；

2012－03－12

湖南省科技计划项目（2009SK3053）；湖南省教育厅重点实验室项目（09K006）

孙鸿睿（1980－），女，博士，研究方向为空间数据数字水印等。＊通讯作者E－mail：cumtyinpc＠163.com