基于动态测量模型的圆度误差分离方法研究*

刘 飞，梁 霖，徐光华，2，针 钊，黄付中

(1.西安交通大学机械工程学院，西安 710049;2.西安交通大学机械制造系统工程国家重点实验室，西安 710054;3.大连机床(数控)股份有限公司技术中心，辽宁 大连 116620)

基于动态测量模型的圆度误差分离方法研究*

刘 飞1，梁 霖1，徐光华1，2，针 钊1，黄付中3

(1.西安交通大学机械工程学院，西安 710049;2.西安交通大学机械制造系统工程国家重点实验室，西安 710054;3.大连机床(数控)股份有限公司技术中心，辽宁 大连 116620)

针对精密加工过程中影响圆度误差分离精度的问题，在轴截面的测量坐标系中，根据传感器和轴截面的运动关系建立起传感器输出的动态测量模型，通过对圆度误差分离算法的推导来研究其近似条件，并分析讨论了角度参数及周期采样点数对误差分离的影响;在此基础上，提出了一种提高分离精度的误差分离方法，并通过实例验证了误差分离的有效性。

圆度误差;误差分离;动态模型

0 引言

圆度误差作为评价圆柱体零件的一个重要指标，在机械产品制造、航空航天和自动化检测领域中起着非常重要的作用。对于精密回转体加工来说，如何有效的控制加工截面的圆度误差将成为保障零件成形质量的基本要求，而误差分离技术可以准确的获得圆度误差值。

从日本学者首次提出三点法圆度误差分离技术(EST)以来，国内外已经有许多学者对圆度误差分离技术进行了大的研究［1-8］，并取得了可喜的研究成果。圆度误差分离技术一般分为反向法、多步法和多点法。由于反向法利用重复定位，获得测量值样本数有限，故不能保障测量精度的一致性;多步法的操作相对复杂，主要用于回转轴重复精度较高的离线测量;而多点法只需零件在传感器的测量范围内做回转运动，不需要对传感器进行转位操作，适合在机测量。为此，许多学者又对圆度误差分离方法进行了进一步的研究。但是，目前的研究缺乏对三点法原理进行深入分析研究及适用条件，这就限制了在机精密圆度误差的检测应用。

本文通过对传感器和轴截面的运动关系，建立起动态测量模型，对三点法误差分离的推导来研究其适用条件，并分析讨论了角度参数及周期采样点数对误差分离的影响;在此基础上，提出了一种提高分离精度的误差分离方法，并通过实例验证了分离的有效性。

1 圆度误差分离的动态测量模型

1.1 三点法圆度误差分离的算法

圆度测量三点法基本原理为:围绕主轴的测量截面上布置交于一点的三个传感器S1、S2和S3，如图1所示，且此三个传感器与水平位置的夹角分别为0°、α 和 β。

图1 三点法传感器布置示意图

那么，以三支传感器的交点为坐标原点建立测量坐标系，那么传感器得到的测量数据分别为:

式中:Sm(θ)为第m个传感器的测量值(m=1、2、3);r(θ)、r(θ+α)和r(θ+β)分别为第m个传感器对应的的圆度误差;δx(θ)和δy(θ)分别为回转误差在X轴和Y轴上的分量。将式(1)中的三组测量值分别乘以权系数a、b、c并相加得到如式(2)所示的组合信号S(θ):

若要分离出圆度误差r(θ)，则需要a+bcosα+ccosβ =0和bsinα +csinβ =0。当取a=1时，求解出a、b、c，并代入式(2)化简可得 S(θ)=ar(θ)+br(θ+α)+cr(θ+β)，其离散化形式为S(i)=ar(i)+br(i+p)+cr(i+q)，其中 i= θN/2π，p= αN/2π，q=βN/2π。根据离散化的傅里叶变换及时延相移特性可得 Sf(k)=rf(k)(1+bej2πpk/N+cej2πqk/N)，其 k=0，1，2，…，N-1，令g(k)=1+bej2πpk/N+cej2πqk/N，则:

其中g(k)为权函数;对其进行傅里叶反变换，可得分离的圆度误差r(i):

1.2 三点法测量的动态模型

上述算法强调的是基本原理，而在测量过程中，由于轴截面的运动，其传感器的输出为动态信号，那么其动态测量模型可以表示如下，仍以三个传感器测量轴线的交点o为坐标原点，建立测量坐标系xoy，某时刻轴截面在测量坐标系中的位置如图2所示。

图中o'为被测截面的回转中心，被测截面的转动角θ= ωt，设∠o'ox=.Ω，r(θ)为被测截面在θ处，截面圆轮廓的回转中心到截面圆轮廓的距离，反映的是圆轮廓信息，δ(θ)为测量截面在转动角度θ后oo'之间的距离，测量时传感器固定，被测对象的运动方向为顺时针旋转，可以看出三个传感器的感知距离分别为oA、oB和oC，根据几何关系三个传感器的输出表达式为:

图2 传感器输出的几何原理

展开得到:

式中:Si(θ)为第 i个传感器的感知量(i=1、2、3);δx(θ)为回转运动误差δ(θ)在测量坐标系xoy中x轴上的分量;δy(θ)为回转运动误差 δ(θ)在测量坐标系xoy中y轴上的分量;r(θ+φi+τi)是和传感器实际数据相关的二乘心到对应截面轮廓的距离(i=1、2、3);Ω是oo'与x轴的夹角，其随着o'位置的不同而变化。而上式中 r(θ+ φi+ τi)的τi(i=1、2、3)为未知变动量，无法得到它与r(θ+φi)之间的关系，因此，当回转误差较小时可用r(θ+φi)代替r(θ+φi+τi)，因为:

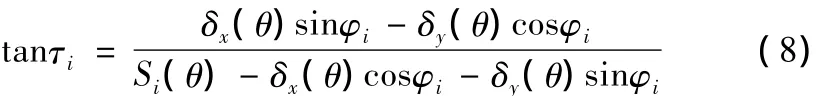
通常Si(θ)和r(θ+φi+τi)为相同数量级，而δ(θ)则要小一个数量级，那么，当 δ(θ)足够小时，τi趋近于0，则上式可化简为:

当各个传感器与水平位置的夹角取φ1=0，φ2= α+φ1=α，φ3=β+φ1=β时，即为式(1)所示的基本方程。

通过上述推导可见，考虑到轴截面的动态运行过程，三点法误差分离方法实际上是圆度误差的近似计算，那么，在实际应用中需要满足上述近似条件才能取得较好的结果。

2 圆度误差分离的影响因素分析

从基本方程可知，若测量参数选择不当也会使圆度误差分离结果失真。而从应用角度来说，传感器角度和周期采样点数无疑是两个重要影响因素。

2.1 角度误差因素影响

由式(3)可以看出，当权函数g(k)=0时，此式是一个不定式，在此情况下使r(k)=0，即圆度误差中第k阶谐波被抑制，便会导致分离结果失真。容易证明总有g(1)=0，即第1阶谐波总是被抑制的，而恰好消除了安装偏心的影响。而当p，q和N具有大于1的公因数w时下式成立。

式中，m为任意整数。因此，只要选择合适的p和q，使得p、q、N三个数有大于1的最大公因数时，就可以使除k=1以外的所有g(k)≠0，从而避免除一阶以外的谐波被抑制掉。而p和q实际反映的是传感器角度α和β，则不同参数选取将影响分离效果。

设截面圆轮廓形状为椭圆，被测对象径向截面的周期采样点数N为256，α =70.3°、β =180°。在此参数设置条件下，其误差分离结果如图3所示，其中黑色曲线为原始圆轮廓，红色圆圈为分离的圆轮廓。由图中的对比可见:分离的圆度轮廓信号并不是很理想，原始和分离的圆轮廓相关系数仅为0.546，分离结果比较差。图4为原始圆轮廓和分离的圆轮廓的频谱对比图，从可以看出:分离出来的圆度轮廓没有完全的包含原来的圆度轮廓信息中所包含的主要频率信息。

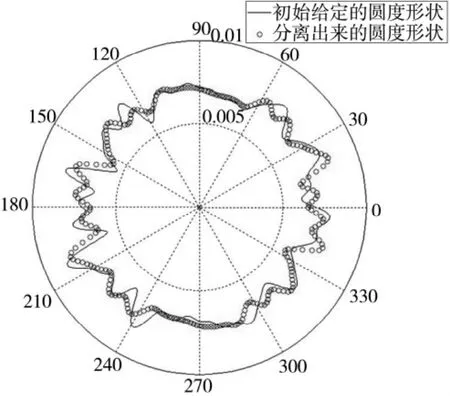
图3 圆轮廓的对比

图4 轮廓的频谱图像对比

用最小二乘圆法对圆度误差进行评定:原始圆轮廓的圆度误差为3.233μm;分离的圆轮廓圆度误差为2.497μm。两个评定结果偏差较大，分离结果失真。

图5所示为该角度参数下对权函数模|g(k)|的影响，其中权函数的模|g(k)|有64个零值，使得圆度轮廓信号中的主要奇次谐波被抑制，因此造成了圆度误差分离的失真。

图5 角度参数对权函数模的变化

若α不变而β=171.6°时，那么它对权函数模的影响如图6所示，由此可见，权函数模|g(k)|的取值很少为零，因此，在此角度参数下权函数不产生谐波抑制，可以提取出理想的圆度误差。

图6 角度参数对权函数模的变化

通过以上分析可知，在实际应用中，需要对角度参数的选取有一个全局性的把握，以避免实际测量时的盲目性。

2.2 周期采样点数误差因素

在实际测量中，机床主轴旋转时往往存在速度波动，即造成周期采样点数存在误差，那么会对谐波一致产生影响。

设定实际周期采样点数N为2048点，而周期点数变化范围为［2020，2070］，即偏差大概在实际点数的百分之一范围内，图7为周期采样点数的误差对误差分离精度的影响变化曲线，图中曲线为分离的圆轮廓和原始圆轮廓的相关系数取值。

由此可见，当计算所用的周期采样点数和实际的周期采样点数都为2048点时，相关系数为0.9929，相似程度较高，误差分离的精度很高，而当使用的周期采样点数大于或小于实际点数时，相关系数都呈现下降趋势，即精度损失呈变大趋势。

图7 周期采样点数误差对分离结果的影响

3 提高分离精度的测量算法

考虑到传感器角度和周期采样点数对分离结果的较大影响，在结合动态测量模型，本文提出了一种提高分离精度的圆度误差分离方法，其基本思想就是在被测件截面上贴装一个磁性金属标记作为测量基准(如图8所示)，以此基准来准确测量周期采样点数和角度值，在此基础上，结合三点法误差分离，可实现圆度误差的有效分离，具体步骤如下:

图8 角度测量示意图

(1)通过数据采集获得时间序列Xi，并对数据波形中的突变点按式(11)计算出被测对象的周期采样点数，其中M为突变点的个数;

(2)分别在传感器S1、S2和S3所采集到的数据中确定突变点A的中心位置。采用式(12)、(13)便可以计算出角度参数pA和qA。

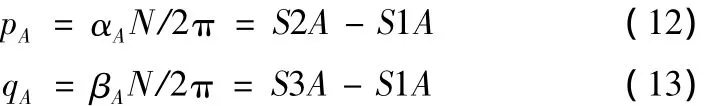
式(12)和(13)中，S1A、S2A和S3A分别为传感器信号中突变点A的中心位置;αA、βA分别为用突变点A确定的传感器S1与S2、S3之间的夹角;pA、qA分别为用突变点A确定的传感器S1与S2、S3之间的夹角参数;

(4)在精确获得传感器角度参数后，根据三点法误差分离方法，计算权函数，并通过傅里叶反变换分离出圆度误差。

4 实验测试分析

为了验证误差分离方法的可行性，现对一直径为40mm的圆柱形棒料进行了实验测试。传感器及安装支架的定位如图9所示，标定好传感器的测量基准，并在被测件上贴上角度标记，机床转速为200 rpm，采样频率为2000Hz。

图9 传感器及保持支架的安装

图10所示为传感器测量波形，其中突变点A为角度标记点，计算得到角度精确的P和Q，进而换算成角度值，即S1与S2之间的夹角.α=118.21°，S1与S3之间的夹角β=241.58°。

图10 传感器夹角的精确测量

对测量的角度参数进行谐波抑制验证，若产生谐波抑制严重，则放弃此角度参数，重新选择传感器安装位置，直到满足测量要求为止。图11所示为测量的角度参数的权函数变化波形，可以看出权函数的模 |g(k)|除了k=1外没有零点，即不会产生谐波抑制作用，所以此角度参数符合测量要求。

最后，通过误差分离计算得到被测件的圆轮廓并将其叠加在测试基圆上，如图12所示。用最小二乘法评定分离出来的圆度误差为41.85μm，为了验证分离结果的可靠性，将此被测对象用圆度仪进行了测量，测量结果为41.37μm，两次测量值偏差为0.5μm。由于传感器分辨率以及传感器安装同心误差的影响，可认为结果基本一致。由此可见，基于三点法圆度误差可实现圆度误差的在机测量。

图11 角度参数谐波抑制检验

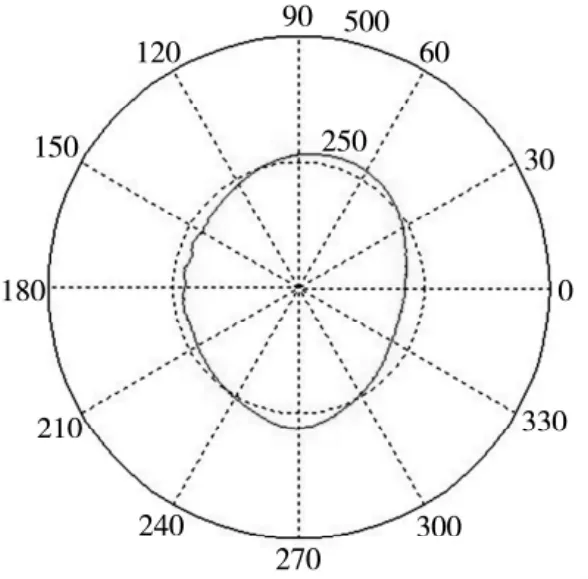
图12 误差分离得到的圆度轮廓

5 结论

对三点法圆度误差分离技术在应用中存在的问题进行了研究与探讨，提出了一种误差分离的模拟与分析方法。并分析讨论了角度参数和周期采样点数对误差分离精度的影响，最后通过实例验证了误差分离的有效性。

［1］Grejda Robert，Marsh Eric，Vallance Ryan.Techniques for calibrating spindleswith nanometer error motion ［J］.Precision Engineering，2005，29(1):113-123.

［2］洪迈生，蔡萍.多步法误差分离技术的比较分析［J］.上海交通大学学报，2004，38(6):877-881.

［3］任东旭，王桂霞，李雪丽.多周法回转误差分离的应用研究［J］. 工具技术，2010，44(5):96-99.

［4］张镭，赵莹，张玉.三测头法误差分离技术的理论与试验［J］. 机械工程学报，2009，45(6):256-261.

［5］刘蜀，韬杨平，康海燕.基于三点法的主轴回转误差二次分离技术［J］.制造技术与机床，2008(2):112-115.

［6］绳飘，张振华.误差分离技术在主轴回转误差检测中的应用［J］. 制造业自动化，2009，31(4):73-74.

［7］丁曙光，李浩，桂贵生.三点法圆度误差分离技术在轴类零件测量中的应用研究［J］.机床与液压，2008，36(2):116-118.

［8］张玉梅，左春柽，李春芳.基于IRM和小波变换的圆度误差在线检测技术［J］.农业机械学报，2009，20(7):212-216.

Study of Roundness Error Separation based on Dynamic Measuring Model

LIU Fei1，LIANG Lin1，Xu Guang-hua1，2，ZHEN Zhao1，HANG Fu-zhong3
(1.School of Mechanical Engineering，Xi’an Jiaotong University，Xi’an 710049，China;2.The State Key Laboratory for Manufacturing Systems Engineering，Xi’an Jiaotong University，Xi’an 710054，China)

Aiming at the accuracy of roundness error separation in precision machining，according to the relationship between axisymmetric body and sensors，the dynamic measuring model for motion of axisymmetric body cross section is built，meanwhile the mathematic expression of sensors output is deduced to analyze the approximate condition of error separation.Then，the effect factors of angular error and periodic sampling error which effect error separation result are discussed.Thus a method of roundness error separation which improving accuracy of separation is proposed，and test results show that the modeling study is very effective for roundness error separation and suppressing effects of errors in workpiece machining.

roundness error;error separation;dynamic model

TH165.3

A

1001-2265(2012)12-0092-04

2012-02-13;

2012-04-12

机床重大专项项目资助(2009ZX04001-051)

刘飞(1979—)，男，河北隆尧人，西安交通大学机械工程学院博士研究生，主要研究方向为机械故障诊断、精密测量技术，(E-mail)lf.7902@stu.xjtu.edu.cn。

(编辑 赵蓉)