声振系统中高频能量流分析法研究进展

游 进，孟 光，李鸿光

(1.中国空间技术研究院 载人航天总体部，北京 100094;2.上海交通大学 机械系统与振动国家重点实验室，上海 200240)

出于经济性要求和减重的考虑，很多产品结构(如汽车、船舶、航空航天器等)采用很多轻薄构件，使得这类结构的中高频减振降噪问题显得较为突出。目前广泛应用于预测复杂结构声振响应的成熟手段主要包括以力和位移为基本变量的有限元/边界元法［1－2］，以及以能量为研究变量的统计能量分析法［3－6］(Statistical Energy Analysis，SEA)。对于传统的有限元/边界元法，由于结构在中高频上的模态波长很小，声振响应建模分析需要划分非常细密的网格，造成计算成本过高。此外，中高频上，结构参数、边界条件及载荷的细微变化均会对结构的位移响应造成显著影响，传统的有限元/边界元法作为一种确定性方法，其计算结果只能视为声振系统所有可能动力响应集合的一个样本，这进一步反映出有限元/边界元在中高频应用上的局限性。SEA法基于结构动力分析的模态方法提出，以耦合结构子系统的空间及频率平均总能量为基本研究变量，并从能量存储、传递和耗散的角度来描述结构的动力行为。SEA采用集总参数模型，所建立的模型规模较小，对于复杂结构，只需用一组线性代数方程便可反映耦合子系统间的能量平衡关系，求解方程便可得到所有子系统的稳态振动能量，因而方法的计算效率很高。经典SEA法的不足之处在于其引入的假设过于苛刻，因此一直以来都有学者质疑其合理性［7－9］，同时这些假设也将SEA法的适用范围限制在高频区域。

为克服现有动力响应预测方法的局限性，学者们基于结构动力分析的波动方法提出了能量流分析法(Energy Flow Analysis，EFA)。能量流分析法基于对结构内传播波功率流传递特性的认识，以在时间和波长距离上平均的能量密度及功率流作为其基本研究变量。通过利用三个基本关系，即:① 简化的功率流－能量密度关系;② 损耗功率－能量密度关系;③ 微元体的能量守恒，可以导出能量流分析法的控制微分方程。能量流分析法以能量密度为变量，因此可以反映动力响应在耦合子系统空间上的分布情况，这与SEA作为集总参数方法只能提供子系统的平均总能量相比，具有很大的优越性。从应用的角度，能量流分析法可以方便地利用有限元法基于声振系统的几何模型对能量密度场进行建模求解，相比于SEA不关注子系统的几何模型细节及载荷位置等信息，能量流分析法可充分地反映几何特征及载荷位置等对声振系统动响应的影响。由于能量流分析法实用上有很大的优点且方法引入的假设条件较少，因此受到很大的关注，提出至今获得了很大的发展，本文基于能量流分析法理论及应用研究的相关文献，系统回顾能量流分析法的发展过程，提炼该方法的理论框架并说明其研究进展。

1 基本能量流分析方程的发展

俄罗斯的一些学者最早从考虑能量密度和功率流在结构内分布的角度来研究结构的动响应问题［10－14］。在这些有关结构内能量流传递特性的早期研究中，结构中不同类型的传播波被假定为互不相干且它们的能量可以叠加，从而导出了类似于热传导的描述结构内能量流分布的微分方程:

Wohlever等［16］针对纵向振动杆和横向振动梁进一步研究了稳态振动结构内的能量传递特性与热传导问题的类比性，并揭示了导出能量流分析微分方程所做近似假设的物理含义。假定杆内存在相向传播的纵波，在小阻尼条件下，由振动位移解导出的相向传播波的功率流和能量密度的解析式表明，功率流与能量密度的梯度成正比，能量由高能量密度区域流向低能量密度区域，即:

式中，q表示同时存在正负向传播波的杆内功率流。式(2)在杆上任意一点均成立，不需做任何假设。对于梁的弯曲振动，由位移解导出的功率流与能量密度解析式表明，类似于式(2)的规律在任意点上并不准确成立，只有忽略了弯曲振动的近场项并将功率流与能量密度在一个波长的局部空间范围上进行平均，才可得到如式(2)的功率传递特性表达式。在波长距离上对解析能量密度和功率流进行平均是一种重要的概念，因为经过空间周期平均后，相同频率的相向传播波的能量密度和功率流等能量变量可以进行叠加，从而使得从能量角度来理解振动问题变得简单。由于这种空间上的周期平均不涉及其它前提假设，因而实质上反映了结构远场传播波稳态功率传递特性的一般规律。

基于对结构内功率流传递基本规律的认识，Bouthier等［17－20］求得了板弯曲振动和张紧膜在时间及波长距离上平均的功率流及能量密度表达式，同时也导出了相应的能量微分方程:

式中:cg为二维结构相应传播波的群速，x为二维结构任意点的位置矢量。上式的导出利用了二维结构内相向平面弯曲波及压缩波的如下简化功率流传递特性:

式中，q为二维结构内的功率流矢量。板的弯曲振动及张紧膜的能量方程均通过与从结构运动方程出发用模态分析法解得的能量响应精确解进行了对比，从而验证了能量流分析法的有效性。在Bouthier等相关研究的基础上，Ichchou［21］对考虑柱面波、球面波和平面波时的能量传递模型进行了一般性总结。

Zhang等［22－23］提出了一种新的推导结构能量流分析微分方程的方法，这种方法视结构中任意方向上的传播波为在两个垂直方向上传播的波的叠加，合成波的能量密度及功率流均由传播方向互相垂直的两个波的能量密度及功率流叠加而成，因而可单独对传播方向垂直的两个波的能量传递特性进行分析，这样做简化了能量流分析微分方程的推导。

Lase等［24］期望提供从能量角度出发描述结构振动的一般性认识，提出了通用能量动力学方法(General Energetic Method，GEM)。这种方法指出结构内分别存在两种能量密度和功率流，其中一种对应于结构的总能量密度和主动能量流(active energy flow)，反映结构内传播波的能量特性，另一种对应于Lagrangian能量密度和被动能量流(reactive energy flow)，反映结构的模态能量特性。两种不同类型的能量密度和能量流均存在控制微分方程，而当忽略近场效应和在波长距离上平均，即可由GEM中描述总能量和主动能量流的方程导出经典的能量流微分方程式(1)。

薄板结构面内纵波和剪切波的能量微分方程由Park等导出［25］，其形式与式(3)一致。由于纵波和剪切波的位移在运动方程中相互耦合，因此，与确立弯曲波的能量传递模型相比，面内波能量传递模型的确立较为复杂。通过引入两个势函数使运动方程所描述的纵向运动和剪切运动解耦，分别导出纵波和剪切波的能量密度和功率流表达式并在一个波长的空间距离进行局部平均，仍可以得到与式(4)一致的简化功率流传递特性。

解妙霞等［26］导出了圆柱壳在轴对称激励下的弯曲振动能量微分方程，由于激励的对称性，所考虑的圆柱壳弯曲运动属一维问题，因而相应的能量微分方程的形式和梁的弯曲振动能量微分方程一致。

对于在垂直方向上具有不同刚度的正交各向异性板，Park等［27］导出了其弯曲波场的能量流分析方程:

式中:cgx和cgy为相互垂直方向上的弯曲波群速。当考虑板为各向同性时，能量方程式(5)简化为式(3)。正交各向异性板的功率流与能量密度关系为:

可见功率流与能量密度的梯度并不直接相关。

薄板弯曲波场能量方程式(3)是基于经典的Kirchhoff板理论导出的，Kirchhoff板理论只用板中面的挠度描述板的运动状态，而在高频上弯曲板的剪切变形和转动惯量的效应非常显著，需用Mindlin板理论对其动力状态进行描述，基于此，Park等［28］导出了均匀Mindlin板的弯曲振动能量流分析方程。在Mindlin板的临界频率以下，板的弯曲振动以挠曲效应为主，其能量方程式与式(3)一致。在Mindlin板的临界频率以上，弯曲振动板包含三种传播波，即面外剪切波(Outof-plane shear wave)，挠曲主导弯曲波(Bending dominant flexural wave)和剪切主导弯曲波(Shear dominant flexural wave)，利用能量流分析理论的空间局部平均的思想，对这三种波场均可导出与式(3)形式一致的能量方程。

Yan［29］研究了能量流分析法在复合层板上的应用，复合层板由多层正交各向异性板以不定向角度层叠而成。由于复合层板为各向异性，传播波的群速呈现各向不同的特点，在假定结构波场为平面波散射波场后，Yan导出了复合层板的弯曲、纵向及剪切波场的能量微分方程:

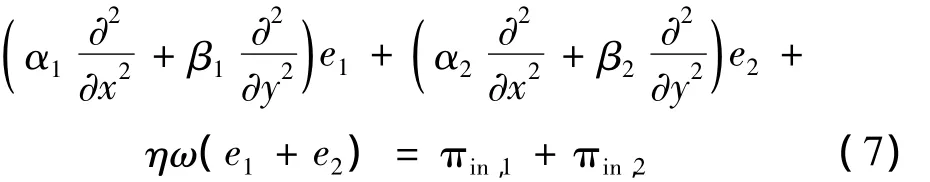
式中:α1，α2，β1和 β2与结构刚度、频率及波数有关。式(7)中，复合层板结构的波场能量为两部分能量之和，对其中的单一能量组分，均存在与之对应的功率流组分，两者间符合与式(4)一致的能量传递关系。

一般地，各种波场的能量流微分方程均利用有限元法求解，很多文献把能量流分析方程的有限元求解方法称为能量有限元分析(Energy finite element analysis，EFEA)。为简化计算，Wang 等［30－32］提出用有限体元法求解能量流分析的基本方程，并称之为零阶能量有限元分析(EFEA0)。该方法的思路是用有限体元对连续能量场进行离散，在单个体元空间上对能量方程进行积分，同时用相邻体元能量的差分代替能量对位置的导数，得到单个体元的能量平衡方程，这一过程消除了原方程中能量变量对位置的二阶微分。Santos［77，78］等采用谱元法求解基本能量流分析方程，提出了能量谱有限元法(Energy spectral element method，ESEM)，该方法可给出能量分析方程的解析解，但适用性有限，很难用于几何非均匀结构和任意边界条件等一般性问题。

2 耦合形式下能量流分析的应用

工程实际中需进行中高频动响应分析的声振系统一般都是较为复杂的耦合系统，可能包含不同子结构间，或结构与流体间的复杂耦合形式。在基本构件的能量微分方程提出后，能量流分析法首先被用于一般的耦合结构上，后又被用于处理结构与流体(包括声场与液体)间的耦合和其它更为复杂的结构耦合形式上。

能量流分析法的基本变量是经空间局部平均的能量密度，因而在耦合结构交界面两边的能量密度不连续。能量流分析法提出后遇到的首要问题是不能将其有效地应用于一般耦合结构，在其发展初期的大多数应用都只针对共线耦合梁等简单耦合情况［16，24，33－34］。要将能量流分析法用于求解一般耦合结构，关键性问题将连接处的功率流传递特性与能量流分析的基本理论进行结合。考虑结构间的耦合关系并将能量流分析法应用于一般耦合结构的方法由Cho等人提出［35－38］，具体过程就是将连接处各波场的能量密度和功率流均视为正负向传播波的能量密度之和和功率流之差，再结合半无限耦合连接的功率传递系数，将连接处各耦合波场的能量密度与功率流联系起来，从而使结构耦合问题得以解决。

Bernhard等［39］总结了将能量流分析应用于一般耦合结构的具体方法，对一个复杂耦合板结构的能量响应进行计算以展示这种方法在处理实际复杂问题上的可行性。Vlahopoulos等［40］基于能量流分析法对复杂船体结构的中高频响应进行了预测。Klos对一个由不同材料组成的共面耦合板的能量响应进行了计算［41］。Borlase等［42］基于能量流分析法对大型复杂结构的阻尼分布进行优化，以达到控制结构某一部分振动能量的目的。Park等［25］对两块耦合矩形板的能量响应进行求解，计算中考虑了面内纵波、剪切波与弯曲波的相互耦合，结果表明，当阻尼很大且分析频率很高时，面内波的能量响应水平与弯曲波的能量响应水平相当。Zhang等［22－23］利用能量流分析法对一个潜艇结构以及小型渔船的能量响应进行了计算，并将结果与用致密有限元网格模型计算的响应以及SEA的计算结果进行了比较，对于分析结构的一些构件，能量流分析法的结果与其它方法的预测结果比较吻合。曾勤谦等［43］利用能量流分析法对一个平面框架结构进行响应预测。孙丽萍等［44－45］将能量流分析法用于船体基座的动响应计算。吴轶钢基于零阶能量有限元分析对加筋板的能量响应进行了求解［46］。

Cho等［35－38］提出的处理耦合结构的方法虽然主要针对由相同结构件组成的耦合系统(如仅由梁或板组成的耦合系统)，但其反映了能量流分析法处理不同波场间耦合问题的一般原理，在其基础上，很多学者作了不同方面的研究，以将能量流分析法的应用拓展至更为一般的耦合形式。Seo等［47］研究了能量流分析法在通过梁连接的耦合板结构上的应用，并对一个含等距排列加强筋的矩形板的能量响应进行求解，与位移解的对比验证了方法的正确性。Vlahopoulos［48－50］将能量流分析法与周期结构理论相结合，对用周期布置的加强筋强化的潜艇结构的动力响应进行了求解并与试验结果进行了对比。

为基于能量流分析法处理声振耦合问题，Bitsie［51］首先导出了声场的能量流分析方程，并在其基础上导出了结构与声场间的耦合关系。声场的能量流分析方程与式(1)式(3)的形式相同，只是其位置矢量为空间三维矢量，声场的功率流也相应地为空间三维矢量。对于弯曲振动平板与声场间的耦合问题，当频率低于板的临界声辐射频率时，结构－声场的耦合关系对平板的作用表现为板上的有效面质量和声辐射阻尼因子，其中声辐射阻尼因子是考虑到有限板的边界声辐射而引入的修正项;当频率高于板的临界声辐射频率时，该耦合关系对平板的作用表现为板上的辐射阻尼因子。考虑了结构－声场耦合关系的结构能量微分方程为:

式中，cg为板中弯曲波的群速，当频率低于临界声辐射频率时，其值受到等效面质量的影响，ηrad为结构－声场间的耦合作用导致的辐射阻尼因子，其表达式为:

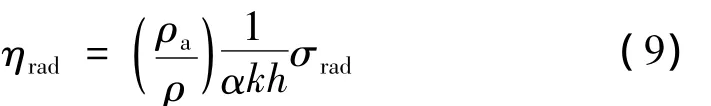
结构－声场间的耦合问题还可利用基于能量流分析与能量边界元分析的混合方法进行处理［54－55］，对于由噪声源引起的结构高频振动，可以通过能量边界元法的计算结果得到噪声源作用于结构的激励，并由此根据能量流分析法计算结构响应。Dong等［56］基于该方法对声振系统的振动及噪声对设计参数的敏感度进行研究，并在其基础上进行优化设计，相关方法被用于汽车及船舶的结构设计，以使结构的高频噪声达到最小。

Zhang等［22，57］研究了能量流分析法在与液体接触的弯曲振动板结构上的应用，与该方法在结构－声场耦合情况下的应用相似，液体与结构间的耦合作用也是根据频率的不同以等效面质量或等效辐射阻尼因子的方式对板的动力特性产生影响，此种情况下，板的能量方程与式(8)相似。由于液体与板间的耦合作用会表现为板结构上的等效面质量，因此与板接触的液体也会改变耦合板结构连接的功率传递特性。此外，他们进一步地将考虑了接触流体作用的能量流分析法应用在一些更复杂的耦合结构上，即还同时考虑了周期排布加强筋或多块板通过公共梁耦合的情况［58－59］，并将其用于预测与流体接触的潜艇外壳的动力响应。

在一定的频率范围内，实际耦合结构的一部分子结构可能只包含少数几个波长(这些结构件称为短件或刚件)，而另一部分子结构可能包含大量波长(这些结构件称为长件或柔件)。考虑到这类结构中的短件适合用基于位移的传统有限元法求解，为预测整个耦合结构的响应，Vlahopoulos等［60－62］提出了结合能量流分析与传统有限元法的混合方法。该方法的主要思路是用动力缩聚得到短件在边界自由度上位移与力间的关系，再考虑力和位移的连续性条件将短件与长件进行耦合。这种方法主要被用来对由短梁连接的两根长梁这一共线耦合梁结构的动力特性进行研究［60－61］。当外载荷作用在长件上时，可以根据短件的动力缩聚模型及边界适应性条件计算出连接短件的功率传递特性，依此功率传递特性用能量流分析法计算长件的能量响应分布并由此确定短件边界上的响应，最后再计算短件的位移响应。当有激励作用在短件上时［62］，短件自身的响应会影响其所代表的连接的功率传递特性，因此需要根据边界适应性条件通过迭代来确定连接特性。这种方法后来被进一步推广应用到平面复杂耦合梁结构上［63］，并考虑了梁连接处弯曲波与纵波间的耦合。由于在计算短件连接的功率流传递特性需利用长件中传播波的解析式，而实际中无法假定具有一般几何特征的长件中传播波的解析式，因此Vlahopoulos等人提出的这种方法局限于应用在平面梁、杆耦合结构上。

为解决一般的刚、柔件耦合结构的响应预测问题，利用模糊结构理论的基本思想［64－66］，Hong 等［67］提出了另一种能量流分析/有限元混合方法。该方法以附加阻尼的方式反映柔件对刚件动响应的影响，其数值基于柔件在连接处的阻抗获得。该方法具体过程是首先通过基于位移的传统有限元法计算刚件的动响应并计算消耗在附加等效阻尼上的功率，以此作为柔件的输入功率，再利用能量流分析法计算柔件上的能量密度分布。利用该方法，Hong等人对多个梁板组合结构的动响应进行了计算。与Vlahopoulos等先前提出的混合方法相比［60－62］，这种方法具有更广泛的适用性。

3 结构的随机能量流分析

能量流分析法提出后在很多实际问题中得到了应用，但是大部分的研究及应用都是针对结构受单频激励的情形，这与能量流分析法的基本原理有关。在推导各种基本结构件及声场的能量流分析基本方程的过程中，均是在假定单频激励激发起单频传播波的情况下，得到了各波场的时间—空间平均功率流与能量密度间的简明关系。实际结构在中高频上所受的激励在很多情况下都是宽带随机激励的形式，对于随机激励下结构的响应预测过去，能量流分析法的应用方式主要有两种:① 按单频激励形式计算结构在分析带宽内多个频率点处的能量响应再对响应进行频率平均;②只在激励带宽的中心频率上预测结构的动力响应。然而，以上两种有关能量流分析法处理随机激励情形的应用在实质上并没有求解结构在随机激励下的响应，其计算结果并不反映结构在随机激励下的绝对响应能量水平。

对于随机激励下能量流分析法的应用，Han等［68－69］曾进行过相关研究。他们导出了单根梁及单块板在随机激励下能量密度的模态分析解析解，同时基于传统的能量流分析法计算结构响应，通过谱积分的方式得到平均能量密度，并主要对结构在较低频的一个频段内的结构能量响应进行分析。Han等所给出的方法应用属于半经验性质，未经严格的推导及证明，很少有后续相关研究及应用。

通过考虑随机激励下结构能量方程中输入功率的表达形式，游进等［70－74］针对梁及板结构系统提出了能量流分析在随机激励下的应用方法，并称之为随机能量流分析(Random energy flow analysis，REFA)。以弯曲振动板为例，稳态随机激励下，板的随机能量流分析方程为:

式中，Πin(x，ω)为稳态随机激励的输入功率谱，E的物理意义为结构能量密度响应谱的空间局部平均值［74］。相应的平均能量密度及功率流分别按以下两式计算:

随机能量流分析方程(10)建立了结构在随机激励下的能量密度响应谱与激励输入功率谱间的关系，其相应的平均能量密度及功率流均需通过对谱进行积分得到(即式(11)、式(12))，这是其应用上与传统能量流分析法处理单频激励情形的不同之处。此外，由于随机激励下的结构响应是非确定性响应，因此随机能量流分析法的计算结果反映的是结构随机能量响应的统计平均值。

随机能量流分析法提出后被用于计算受随机激励的平面框架结构［70］、空间框架结构［71］及耦合板结构［72－73］的能量响应及功率流。游进等［75］将随机能量流分析法用于计算受随机激励的单根梁的能量密度和功率流，并通过与模态分析精确解进行对比，表明分析频带所包含的模态数而非常宽是影响该方法预测精度的重要因素，在分析频带模态数足够大的情况下，该方法可以在广阔的频率范围上有效预测单系统的能量密度及功率流。

能量流分析和SEA都是基于能量的动力响应预测方法，两种方法间必然存在一定的联系。SEA由于采用的是受独立噪声激励的线性保守耦合振子的功率传递模型［3］，且由于其所采用的基本假设的关系，适于求解受非相关随机激励的耦合结构的动响应［4］，其求解结果反映的是耦合结构随机激励下的稳态响应。传统的能量流分析法主要用于计算单频激励下的动力响应，因此在过去的研究中，两种方法间并未建立起直接联系，两种方法计算结果的对比从未直接针对子系统的能量响应，而是间接地针对不同子系统响应能量的比值［23，40，57，76］。考虑到随机能量流分析可计算耦合结构在随机激励下的能量响应，游进等［74］以耦合梁结构为模型建立了随机能量流分析与SEA间关于能量和功率流变量间的直接关系。

随机能量流分析与SEA虽分别从波及模态的角度定义各自的子系统，但它们所定义的子系统从本质上是一致的，若用两种方法对同一耦合结构进行分析，则对相同的子系统，两种方法预测的子系统总能量应近似相等，即:

随机能量流分析与SEA所描述的子系统间功率流的不同点体现在两点上:① SEA是集总参数方法，其计算的功率流为集总参数，随机能量流分析建立分布式模型，可以预测功率流在子系统内的分布，而只有子系统边界上的功率流直接反映了耦合子系统间的功率传递作用;② SEA与随机能量流描述的子系统间功率流的方式有所不同:SEA处理的是任意一对耦合子系统间的功率流，随机能量流分析只给出流入或流出某个子系统的功率流而不区分流入功率的来源和流出功率流的接受源。

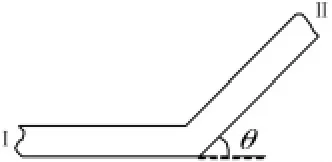
图1 平面耦合梁结构Fig.1 Planar beam junction

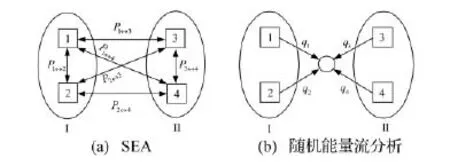
图2 功率流模型Fig.2 Energy flow models

随机能量流分析与SEA间关于功率流变量间的关系可以平面耦合梁(如图1)为模型进行说明。该耦合结构包含弯曲波与纵波间的耦合，以子系统1和2代表梁I的弯曲波和纵波子系统，以子系统3和4代表梁II的弯曲波和纵波子系统，则随机能量流分析和SEA所采用的功率流模型如图2所示。图中Pi↔j是SEA计算的子系统i与j间功率流的大小。qi是随机能量流分析法预测的子系统i在其与其它子系统耦合边界上的功率流。根据图2，可得到两种方法预测的子系统间功率流的关系为:

式(13)、式(14)反映了随机能量流分析和SEA所定义的响应能量及功率流变量的不同点，同时也建立了两种方法关于能量和功率流变量间的直接关系，实质上是将两种方法从研究变量的角度进行统一。基于此，对于任意受随机激励的耦合结构，可对两种方法计算的能量响应和功率流进行直接对比分析。

此外，文献［71］针对一维结构的功率流特性指出，随机能量流分析反映的弯曲波场功率流特性与SEA中的耦合振子间的功率流特性是相似的，而前者所反映的纵波场及扭转波场的功率流特性则无法由后者所采用的耦合振子功率流特性表达。

4 结论

经过二十多年的发展，能量流分析的相关研究获得了较大进展。基本结构件及一些复合结构的各种波场及声场的能量流分析基本方程已被建立起来。对于声振耦合系统，能量流分析法不仅可用于存在不同波场间耦合的复杂耦合结构上，而且可以预测结构－流体耦合系统的动力响应，还可与其它方法相结合以处理一些具体的复杂耦合问题，体现出能量流分析法良好的适用性。此外，随机能量流分析法解决了随机激励下声振系统能量密度响应及功率流的计算问题，同时，随机能量流分析与经典SEA间的区别和理论关联也在一定程度上得到确认。目前，能量流分析理论的一个不足是方法特性研究还不够深入完善，需要进一步系统研究影响方法使用范围和预测精度的各种因素，以便于方法的广泛应用。

［1］ Banerjee P K，Butterfield R.Boundary Element Methods in Engineering Science［M］.UK:McGraw-Hill Book Company，1981.

［2］Zienkiewicz O C，Taylor R L.The finite element method volume 1: the basis［M］. Boston: Butterworth-Heinemann，2000.

［3］Lyon R H，DeJong R G.Theory and application of statistical energy analysis ［M］. Boston: Butterworth-Heinemann，1995.

［4］ Fahy F J.Statistical energy analysis:a critical overview［J］.Philosophical Transactions of the Royal Society:Physical and Engineering Sciences，1994，346(1681):431 －447.

［5］ Heckl M，Lewit M.Statistical energy analysis as a tool for quantifying sound and vibration transmission paths［J］.Philosophical Transactions of the Royal Society:Physical and Engineering Sciences，1994，346(1681):449－464.

［6］ Heron K H.Advanced statistical energy analysis［J］.Philosophical Transactions of the Royal Society:Physical and Engineering Sciences，1994，346(1681):501－510.

［7］ Mace B R.On the statistical energy analysis hypothesis of coupling power proportionality and some implications of its failure［J］.Journal of Sound and Vibration，1994，178(1):95－112.

［8］ Fahy F J.Statistical energy analysis:a wolf in sheep＇s clothing［C］. Proceedings of the Internoise. Leuven，Belgium，1993.

［9］Culla A，Sestieri A.Is it possible to treat confidentially SEA the wolf in sheep＇s clothing［J］.Mechanical Systems and Signal Processing，2006，20(6):1372－1399.

［10］Belov V D，Rybak S A.Applicability of the transport equation in the one-dimensional wave-propagation problem［J］.Journal of Soviet Physics Acoustics，1975，21(2):110－114.

［11］Belov V D，Rybak S A，Tartakovskii B D.Propagation of vibrational energy in absorbing structures［J］.Journal of Soviet Physics Acoustics，1977，23(2):115 －119.

［12］ Buvailo L E，Ionov A V.Application of the finite element method to the investigation of the vibroacoustical characteristics of structures at high frequency［J］.Journal of Soviet Physics Acoustics，1980，26(4):277 －279.

［13］ Butlitskaya I A，Vyalyshev A I，Tartakovskii B D.Propagation of vibrational and acoustic energy along a structure with losses［J］.Journal of Soviet Physics Acoustics，1983，29(4):333－334.

［14］ Nikiforov A S.Estimating the intensity of structure-borne noise in ribbed structures［C］.Proceedings of the 3rd international congress on intensity techniques， Senlis，France，1990.

［15］ Nefske D J，Sung S H.Power flow finite element analysis of dynamic systems:Basic theory and application to beams［J］.Journal of Vibration，Acoustics，Stress，and Reliability in Design，1989，111(1):94－100.

［16］ Wohlever J C，Bernhard R J.Mechanical energy flow models of rods and beams［J］.Journal of Sound and Vibration，1992，153(1):1－19.

［17］ Bouthier O M，Bernhard R J.Simple models of energy flow in vibrating membranes［J］.Journal of Sound and Vibration，1995，182(1):129－147.

［18］ Bouthier O M，Bernhard R J.Simple models of the energetics of transversely vibrating plates［J］.Journal of Sound and Vibration，1995，182(1):149－164.

［19］ Bouthier O M.Energetics of vibrating systems［D］.Purdue University，1992.

［20］ Bouthier O M，Bernhard R J.Models of space-averaged energetics of plates［J］.AIAA Journal，1992，30(3):616 －623.

［21］ Ichchou M N，Jezequel L.Comments on simple models of the energy flow in vibrating membranes and on simple models of the energetics of transversly vibrating plates［J］.Journal of Sound and Vibration，1996，195(4):679－685.

［22］Zhang W.Energy finite element method for vibration analysis of stiffened plates under fluid loading［D］.University of Michigan，2003.

［23］Zhang W，Wang A，Vlahopoulos N.An alternative energy finite element formulation based on incoherent orthogonal waves and its validation for marine structures［J］.Finite Elements in Analysis and Design，2002，38(12):1095－1113.

［24］Lase Y，Ichchou M N，Jezequel L.Energy flow analysis of bars and beams:theoretical formulations［J］.Journal of Sound and Vibration，1996，192(1):281－305.

［25］ Park D H，Hong S Y，Kil H G，et al.Power flow model and analysis of in-plane waves in finite coupled thin plates［J］.Journal of Sound and Vibration，2001，244(4):651 －668.

［26］解妙霞，陈花玲，吴九汇.圆柱壳高频弯曲振动的能量有限元分析［J］.西安交通大学学报，2008，42(9):1113－1116.

［27］Park D H，Hong S Y，Kil H G.Vibrational energy flow models of finite orthotropic plates［J］.Shock and Vibration，2003，10(2):97－113.

［28］ Park Y H，Hong S Y.Vibrational power flow models for transversely vibrating finite Mindlin plate［J］.Journal of Sound and Vibration，2008，317(3－5):800－840.

［29］ Yan X.Energy finite element analysis developments for high frequency vibration analysis of composite structures［D］.The University of Michigan，2008.

［30］ Wang S.High frequency energy flow analysis methods:Numerical implementation，applications，and verification［D］.Purdue University，2000.

［31］ Wang S，Bernhard R J.Theory and applications of a simplified energy finite element method and its similarity to SEA［J］.Noise Control Engineering Journal，2002，50(2):63 －72.

［32］ Marburg S，Nolte B.Computational acoustics of noise propagation in fluids-finite and boundary element methods［J］.Germany:Springer Berlin Heidelberg，2008.

［33］ Stiehl A L.Power flow analysis of beam members with multiple wave types［J］.Finite Elements in Analysis and Design，1996，21(4):253－264.

［34］ Nefske D J，Sung S H.Power flow finite element analysis of dynamic systems:basic theory and application to beams［J］.Journal of Vibration，Acoustics，Stress，and Reliability in Design，1989，111(1):94－100.

［35］ Cho P E.Energy flow analysis of coupled structures［D］.Purdue University，1993.

［36］ Cho P E，Bernhard R J.A simple method for predicting energy flow distribution in frame structures［C］.in Proceedings of the 4th International Congress on Intensity Techniques.Senlis，France，1993.

［37］ Cho P E，Bernhard R J.Energy finite element method for coupled structures［J］.Yokohama，Japan，1994.

［38］ Cho P E，Bernhard R J.Energy flow analysis of coupled beams［J］.Journal of Sound and Vibration，1998，211(4):593－605.

［39］ Bernhard R J，Huff J E.Structural-acoustic design at high frequency using the energy finite element method［J］.Journal of Vibration and Acoustics，Transactions of the ASME，1999，121(3):295－301.

［40］Vlahopoulos N，Garza-Rios L O，Mollo C.Numerical implementation，validation，and marine applications of an energy finite element formulation［J］.Journal of Ship Research，1999，43(3):143－156.

［41］ Klos J.Modeling point excited plates using an energy finite element method［C］.The 2004 National Conference on Noise Control Engineering［J］.Baltimore，Maryland，2004.

［42］Borlase G A，Vlahopoulos N.Energy finite element optimization process for reducing high-frequency vibration in largescale structures［J］.Finite Elements in Analysis and Design，2000，36(1):51－67.

［43］曾勤谦，华宏星，韩祖舜.耦合结构中的功率流有限元法［J］.上海交通大学学报，2000，34(4):503－506.

［44］孙丽萍，聂 武.能量有限元法在船舶结构中的应用［J］.哈尔滨工业大学学报，2008，40(9):1491－1494.

［45］孙丽萍.能量有限元法研究及其应用［D］.哈尔滨:哈尔滨工程大学，2004.

［46］吴轶钢.零阶能量有限元方法及其在船舶结构声辐射中的应用研究［D］.武汉:武汉理工大学，2008.

［47］Seo S H，Hong S Y，Kil H G.Power flow analysis of reinforced beam-plate coupled structures［J］.Journal of Sound and Vibration，2003，259(5):1109－1129.

［48］ Vlahopoulos N.Energy finite element analysis for computing the high frequency vibration of the aluminum testbed cylinder and correlating the results to test data［J］.NASA/CR-2005－213760，2005.

［49］ Vlahopoulos N，Wang A，Wu K.An EFEA formulation for computing structural response of complex structures［C］.Proceedings of ASME 2005 International Mechanical Engineering Congress and Exposition.Orlando，USA，2005.

［50］Zhang G，Vlahopoulos N.Validation of an EFEA formulation for computing the vibrational response of complex structures［C］.Proceedings of 2007 SAE Noise and Vibration Conference.Traverse city，USA，2007.

［51］ Bitsie F.The structural-acoustic energy finite-element method and energy boundary-element method［D］.Purdue University，1996.

［52］ Dong J，Choi K K，Wang A，et al.Parametric design sensitivity analysis of high-frequency structural-acoustic problems using energy finite element method［J］.International Journal for Numerical Methods in Engineering，2003，62(1):83－121.

［53］ Moens I，Vandepitte D，Sas P.Vibro-acoustic energy flow models implemented by finite elements［M］.Leuven，Belgium，1998.

［54］Vlahopoulos N，Zhang G，He J.Combining an energy boundary element with an energy finite element analysis for airborne noise simulations［C］.Proceedings of 2007 SAE Noise and Vibration Conference.Traverse City，USA，2007.

［55］Vlahopoulos N，Li S，Sun J.Combining energy boundary element and energy finite element simulations for airborne noise analysis［J］.Proceedings of 2006 ASME International Mechanical Engineering Congress and Exposition.Chicago，Illinois，USA，2006.

［56］ Dong J，Choi K K，Vlahopoulos N，et al.Sensitivity analysis and optimization using energy finite element and boundary element methods［J］.AIAA Journal，2007，45(6):1187 －1198.

［57］ Zhang W，Wang A，Vlahopoulos N，et al.High-frequency vibration analysis of thin elastic plates under heavy fluid loading by an energy finite element formulation［J］.Journal of Sound and Vibration，2003，263(1):21－46.

［58］ Zhang W，Wang A，Vlahopoulos N，et al.A vibration analysis of stiffened plates under heavy fluid loading by an energy finite element analysis formulation［J］.Finite Elements in A-nalysis and Design，2005，41(11－12):1056－1078.

［59］ Zhang W，Vlahopoulos N，Wu K.An energy finite element formulation for high-frequency vibration analysis of externally fluid-loaded cylindrical shells with periodic circumferential stiffeners subjected to axi-symmetric excitation［J］.Journal of Sound and Vibration，2005，282(3－5):679－700.

［60］ Vlahopoulos N，Zhao X.Basic development of hybrid finite element method for midfrequency structural vibrations［J］.AIAA Journal，1999，37(11):1495 －1505.

［61］Vlahopoulos N，Zhao X.An investigation of power flow in the mid-frequency range for systems of co-linear beams based on a hybrid finite element formulation［J］.Journal of Sound and Vibration，2001，242(3):445－473.

［62］Zhao X，Vlahopoulos N.A hybrid finite element formulation for mid-frequency analysis of systems with excitation applied on short members［J］.Journal of Sound and Vibration，2000，237(2):181－202.

［63］ Zhao X，Vlahopoulos N.A basic hybrid finite element formulation for mid-frequency analysis of beams connected at an arbitrary angle［J］.Journal of Sound and Vibration，2004，269(1－2):135－164.

［64］ Soize C.A model and numerical method in the medium frequency range for vibroacoustic predictions using the theory of structural fuzzy［J］.Journal of the Acoustical Society of A-merica，1993，94(2):849 －865.

［65］ Soize C.Reduced models in the medium-frequency range for general external structural-acoustic systems［J］.Journal of the Acoustical Society of America，1998，103(3):3393－3406.

［66］ Soize C，Bjaoui K.Estimation of fuzzy structure parameters for continuous junctions［J］.Journal of the Acoustical Society of America，2000，107(4):2011－2020.

［67］Hong S B，Wang A，Vlahopoulos N.A hybrid finite element formulation for a beam-plate system［J］.Journal of Sound and Vibration，2006，298(1－2):233－256.

［68］ Han F，Bernhard R J，Mongeau L G.Energy flow analysis of vibrating beams and plates for discrete random excitations［J］.Journal of Sound and Vibration，1997，208(5):841－859.

［69］ Han F，Mongeau L G，Bernhard R J.Energy flow analysis of beams and plates for random distributed loading［J］.Journal of Fluids and Structures，1998，12(3):315 －333.

［70］游 进，孟 光，李鸿光，等.随机激励下框架梁结构能量有限元分析［J］.上海交通大学学报，2009，43(10):1632－1635.

［71］游 进，孟 光，李鸿光.三维框架结构随机能量流分析［J］.上海交通大学学报，2010，44(8):1150－1154.

［72］游 进，李鸿光，孟 光.耦合板结构随机能量有限元分析［J］.振动与冲击，2009，28(11):43－46.

［73］游 进，孟 光，李鸿光.L型耦合板相关激励下高频随机能量流分析［J］.振动工程学报，2010，23(1):60－63.

［74］ You J，Meng G，Li H G.Random energy flow analysis of coupled beam structures and its correlation with SEA［J］.Archive of Applied Mechanics，2011，81(1):37－50.

［75］You J，Li H G，Meng G.Validity investigation of random energy flow analysis for beam structures［J］.Shock and Vibration，2011，18(1－2):269－280.

［76］ Vlahopoulos N，Zhang W.Validation of the EFEA method through correlation with conventional FEA and SEA results［J］.Proceedings of 2001 SAE Noise and Vibration Conference.Grand Traverse，USA，2001.

［77］Santos E R O.High frequency vibration analysis by energy methods［D］.State University of Campinas，2006.

［78］ Santos E R O，Arruda J R F，Dos Santos J M C.Modeling of coupled structural systems by an energy spectral method［J］.Journal of Sound and Vibration，2008，316(1－5):1－24.