新型近等强度高阻尼航天载荷隔振器研究

张针粒，李世其，朱文革，胡线会，祁 宙，马天阳，王 跃，，刘志敏

(1.华中科技大学 机械科学与工程学院，武汉 430074;2.北京空间机电研究所，北京 100076)

航天载荷在运送至预定轨道的过程中，振动环境相当恶劣，受到多种静态和动态载荷。从频谱的分布来看，振动载荷包含几十赫兹，到几千赫兹的低中高频振动与冲击。航天载荷故障约45%正是由发射过程中的振动造成的［1］。采用减振技术，改善航天载荷的振动环境，可降低设计难度与风险、减少成本。

航天载荷隔振一般通过两种途径实现:

(1)替换原适配器为具有隔振性能的适配器［4］。这种方法不需要改变原有接口，但设计范围限制在阻尼材料的贴附形式。

(2)在星箭之间安装隔振器。这类隔振器按是否包含有源控制可分为主动隔振器和被动隔振器。主动隔振器隔振效果显著，但在承载能力、功率、可靠性等方面存在着不足，未见针对发射阶段隔振的实际应用案例［5］;被动隔振器结构形式简单可靠，开发周期短，成本低。国内外已有很多研究与成功应用的报道［5－6］。国外被动隔振器的典型代表如美国CSA公司SoftRide UniFlex/MultiFlex［6］整星隔振器，已多次在实际发射中使用，取得了显著的隔振、缓冲效果。国内的如由张军等［7］设计的整星隔振器，通过有限元分析与振动试验表明，该隔振器可有效地隔离卫星在宽频带上横向和纵向振动。

经研究发现以上提到的典型整星隔振器主要有以下不足:

(1)隔振器支架水平部分的等厚度设计存在应力分布不均现象，安全系数有明显提高空间，由于发射振动环境带有随机性，这种提高对航天发射的高可靠性要求显得尤为必要。

(2)隔振器阻尼耗能较小。以张军等［7］设计的整星隔振器为例，其阻尼比约为0.05。美国CSA公司［8］SoftRide MultiFlex整星隔振器结构与张军等设计的整星隔振器结构相当接近，因此阻尼比应比较接近。由于发射振动环境的幅值高、频率范围宽，当激起共振时阻尼比小的隔振器不能有效地抑制共振峰，即使没有发生失效，其安全裕度也较小。同时，适当提高阻尼比也有利于冲击衰减［9］。从抑制共振提高安全裕度和衰减冲击的角度看隔振器阻尼比需提高。

文中首先分析了航天发射环境对隔振器的设计要求，所设计新型隔振器特点。然后针对隔振器的支架设计，引入了等强度理论，设计了变厚度隔振器支架，对比分析了改进前后支架应力状态。针对隔振器阻尼材料的设计，应用阻尼材料能量耗散理论及Rongong修正模态应变能方法，设计了新颖的梳状剪切型阻尼结构，仿真分析了所达到的阻尼效果。最后，通过由30个隔振器组成的隔振系统的正弦扫频与随机振动试验验证了隔振器性能。

1 新型近等强度高阻尼隔振器简介

根据航天领域应用的特殊性与发射阶段振动环境的特点，分析航天载荷隔振器设计需求，可归纳为:

(1)发射阶段振动力学环境存在不确定性，为此，隔振器应具有高安全系数，航天机械结构一般要求安全系数4以上，愈高愈好;

(2)发射阶段振动力学环境所含频率范围宽广，尤其在低频段模态分布密集，容易激起共振，隔振器应具有较高阻尼，以抑制共振;

(3)在中高频段，有效降低加速度响应均方值，以达到良好的衰减振动的作用;

(4)发动机点火、级间分离等事件伴随有冲击载荷，考虑到高可靠性要求，隔振器应设计冲击保护机制。

考虑到以上航天载荷隔振器设计要求，所设计的新型隔振器(发明专利号:101392808)见图1、图2。隔振器支架由钛合金TC4经慢走丝线切割整体式一次加工而成。自研以丁基为主的高阻尼材料硫化粘结在隔振器支架上。与前文提到的典型隔振器相比，主要具有以下特点:

(1)隔振器金属支架基于等强度理论的变厚度设计(详见第二节)，安全系数明显提高;

(2)新颖的梳状剪切型阻尼结构设计，隔振器等效阻尼比大幅提高;

(3)硬弹簧特性冲击保护设计。当隔振器受冲击压缩变形超过5 mm时，冲击保护槽开始发挥作用，变形愈大，阻尼材料的超弹性限位力愈显著，具有硬弹簧特性，既发挥了冲击保护的功能，又避免了金属支架间的刚性碰撞(刚性碰撞可能使支架产生潜在裂纹甚至破坏);

(4)无缝硫化设计。约束阻尼型隔振器或类似结构存在一个工艺方面需要解决的难点，即确保在反复的振动循环中，阻尼材料与金属支架保持牢固粘结。所设计新型隔振器由整体式模具在高温高压下压注阻尼材料硫化而成，消除了主要剪切耗能阻尼材料与金属支架梳状齿之间的接缝。同时，金属支架硫化表面喷砂处理。经此改进后的试验再没观察到阻尼材料剥离现象。

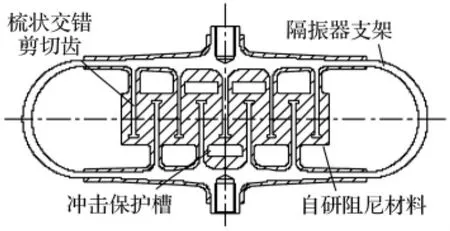
图1 新型航天载荷隔振器剖视图Fig.1 Sectional view of new spacecraft payload isolator

图2 新型航天载荷隔振器实物图Fig.2 Photo of new spacecraft payload isolator

2 隔振器支架近等强度优化

前文提到的典型整星隔振器支架结构，都非常相似，由钛合金材料制作成矩形空心隔振器支架，支架上下水平部分贴敷约束阻尼层，钛合金支架水平部分的弯曲变形带动阻尼层变形，形成阻尼作用。依此建立的隔振器支架组合梁简化模型如图3所示。

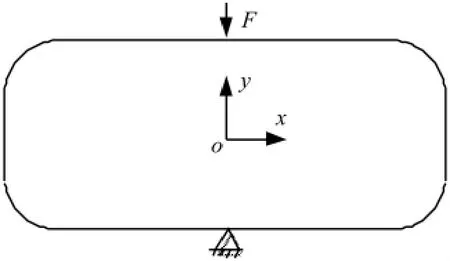
图3 隔振器支架组合梁模型Fig.3 Composite beam model of isolator’s bracket

注意到梁模型的对称性，可以只研究其四分之一模型，如图4所示。

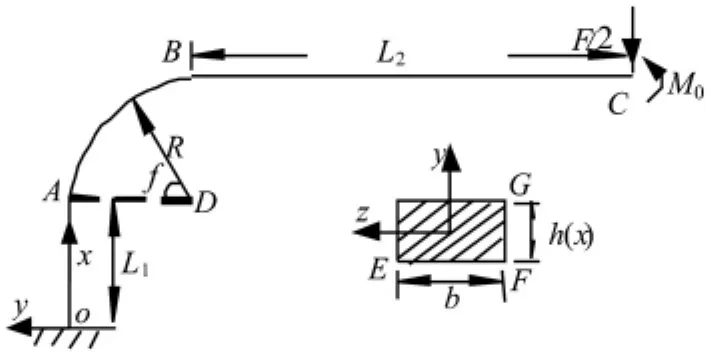
图4 隔振器支架组合梁四分之一模型Fig.4 Composite beam model of isolator’s quarter bracket

等强度设计先针对隔振器的纵向(y向)载荷。横向(x或z向)载荷对隔振器的作用不仅与单个隔振器有关，还与整个隔振系统的布局形式有关，通常是先根据纵向载荷设计隔振器参数，再整体验证隔振系统横向特性(见隔振系统试验)。由隔振器支架尺寸比例知，纵向载荷对隔振器支架的主要作用是弯曲正应力，剪应力远小于正应力，可先依据正应力要求设计隔振器支架，然后校验剪应力强度要求。理想的隔振器支架等强度设计应使支架截面上最大弯曲正应力满足:

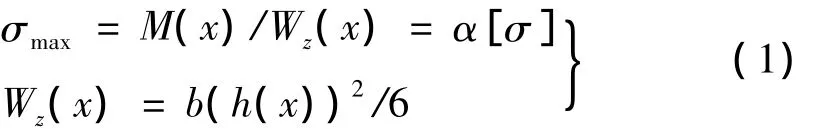
式中，σmax为截面最大弯曲正应力;M(x)为弯矩方程;Wz(x)为矩形抗弯截面系数;［σ］为材料许用正应力;α为安全系数。

由材料力学知，在小变形假设及忽略轴力的情况下梁的扰度微分方程为［10］:

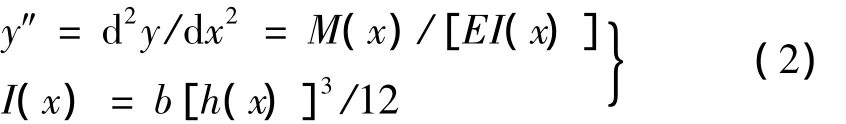
式中，y(x)为扰度方程;E为材料弹性模量;I(x)为梁截面惯性矩。

固有频率是隔振器设计恰当与否的关键，过低固有频率将导致相行程增大，可能造成干涉，同时火箭要求载荷的固有频率不能低于某一下限;过高固有频率不能取得期望的隔振效果。分析图4所示模型，可依固有频率公式［11］推得:

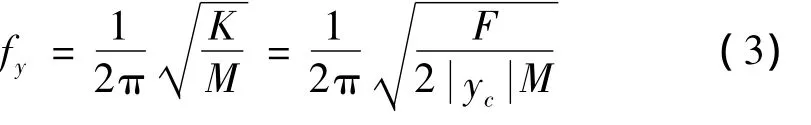
式中，fy为纵向固有频率;K为隔振器纵向刚度;M为单个隔振器额定载荷质量;F为某一施加在C点的载荷;yc为由载荷F引起的C点纵向位移。

联立式(1)～式(3)即可解得等强度厚度方程h(x)关于设计参数 L1，R，L2，b，α，［σ］，f，M 的方程。为防止截面厚度为零的情况出现，有必要进一步依式(4)校核最大剪应力强度条件，对h(x)进行修正。

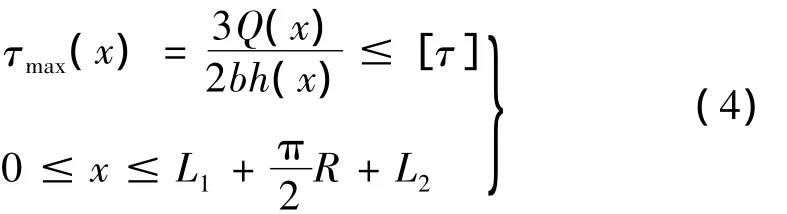
式中，τmax(x)为x处最大剪应力;Q(x)为 x处剪力;［τ］为材料许用剪应力。

为验证所提的隔振器支架等强度设计方法及达到的效果，设计了非等强度与等强度隔振器支架结构。为具有对比性，已使隔振器支架的性能参数保持一致(见表1)。非等强度与等强度隔振器支架示例结构有限元模型如图5、图6。

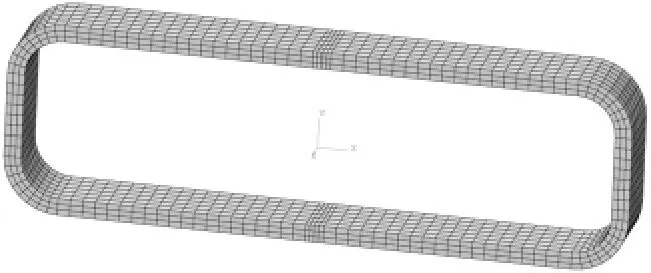
图5 非等强度隔振器支架示例结构有限元模型Fig.5 FEM model of traditional isolator’s bracket

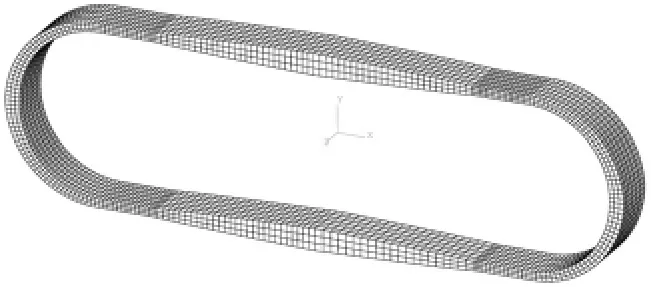
图6 等强度隔振器支架示例结构有限元模型Fig.6 FEM model of equal strength isolator’s bracket

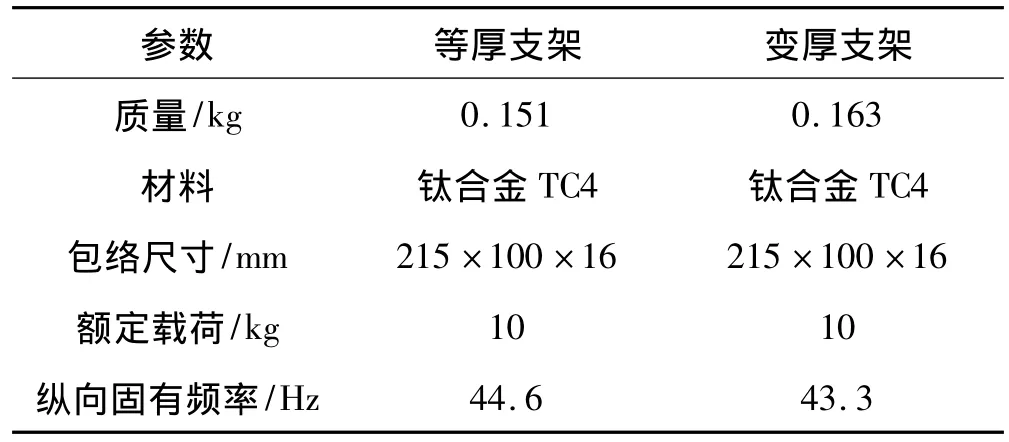
表1 两种隔振器支架的参数Tab.1 Parameters of two isolators’brackets

非等强度与等强度隔振器支架截面最大应力在图4所示曲线坐标系下的分布如图7、图8所示，从中可以得出以下结论:

(1)传统非等强度隔振器支架应力不均，材料强度没有充分挥发作用;

(2)应用等强度设计方法的预测结果与有限元分析的结果比较一致，有限元分析的等强度结构在h(x)=0附近应力有一个下凹的尖峰，这是因为实际等强度结构在h(x)=0附近做了圆整处理;

(3)应用等强度设计方法后，除h(x)=0附近外基本实现了应力均匀分布;

(4)有限元分析表明，等强度设计方法的应用使隔振器支架应力峰值降低了28.9%，即安全系数在原有基础上提高了0.4倍。

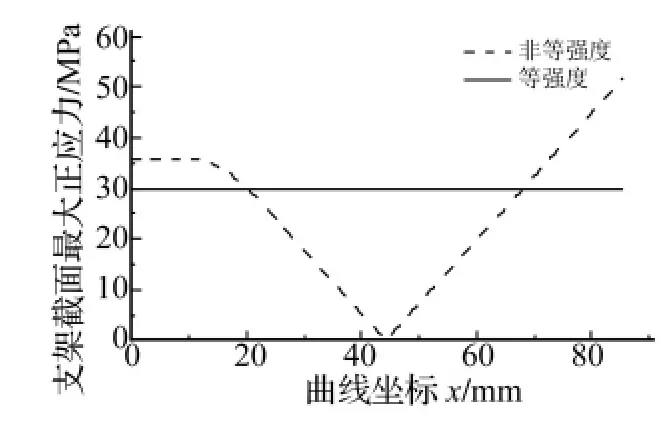
图7 非等与等强度隔振器截面应力对比(力学模型预测)Fig.7 Sectional stress of two isolators’brackets(by mathematic model)

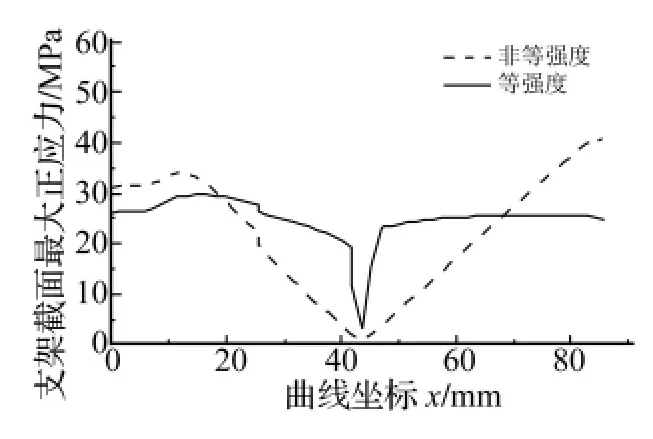
图8 非等与等强度隔振器截面应力对比(有限元分析)Fig.8 Sectional stress of two isolators’brackets(by FEA)

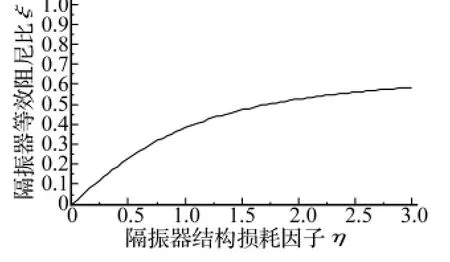
图9 隔振器等效阻尼比与结构损耗因子关系曲线Fig.9 Equivalent damping ratio vs loss factor of isolator

3 隔振器高阻尼比优化

在设计具有高阻尼的隔振器时，应用阻尼比约为损耗因子一半的近似关系的会导致误差过大，所以采取式(5)计算等效阻尼比［12］:

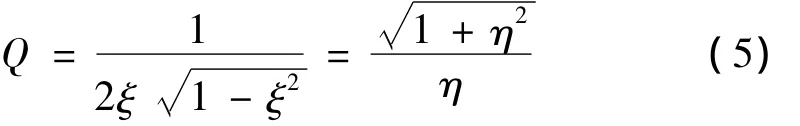
式中，Q为品质因子;ξ为隔振器等效阻尼比;η为隔振器损耗因子。

由式(5)可得隔振器等效阻尼比关于结构损耗因子的关系曲线如图9，为单调递增关系，但递增速率逐渐减缓。

从图9可以看出，隔振器等效阻尼比的提高需增大结构损耗因子。损耗因子可用模态应变能方法方便地计算获得，当损耗因子较大时，传统的模态应变能方法方误差增大。Torvik等［13］通过对比研究发现，Rongong的修正方法是同类修正方法中最精确的，损耗因子计算式为［14］:

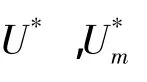
由式(6)可知，提高隔振器损耗因子有两个途径:提高材料损耗因子以及阻尼材料应变能比例。前者由阻尼材料参数决定，后者由选材及隔振器结构设计决定，所设计的新型隔振器在这两方面均做了改进。

首先，在阻尼材料设计方面，自行配制并优选了以丁基为主的高阻尼材料，其50 Hz下动态机械分析(DMA)扫温曲线见图10，在6℃ ～60℃范围内损耗因子高于0.5，30.5℃下达到峰值 0.87，与隔振器工作温度范围20℃ ～40℃相当吻合，使阻尼材料耗能特性得

到充分利用。

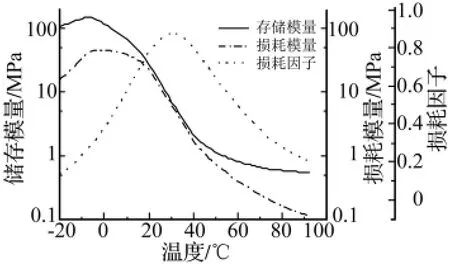
图10 阻尼材料50Hz下DMA测试曲线Fig.10 DMA test of damping material under excitation with 50 Hz

然后，在隔振器阻尼结构设计方面，由简谐激励下阻尼材料每周期耗能公式(7)知，阻尼耗能效果除了与材料参数Gl(ω)有关外，还与阻尼材料的剪应变幅值及产生应变的材料体积有关。

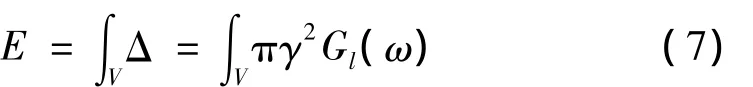
式中，E是每周期阻尼材料损耗能量;Δ是单位体积每周期损耗能量;V是阻尼材料体积;γ是剪应变幅值;Gl(ω)是阻尼材料在频率 ω下的损耗模量，是材料参数。

根据式(7)，在隔振器近等强度支架上，设计了梳状剪切齿(见图1)，该结构可使纵向振动转化为阻尼材料以剪应变为主的变形。同时，与约束薄层阻尼结构相比，大幅增加了阻尼材料用量。

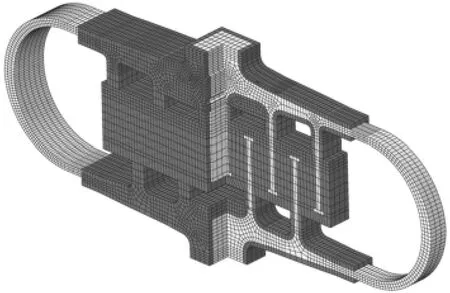
图11 隔振器有限元模型剖视图Fig.11 Profile view of isolator’s FEM

为验证以上在阻尼材料和结构形式方面的优化实现的效果，对隔振器进行仿真分析，有限元模型如图11、图12所示，其中隔振系统由30个均匀圆周布局的隔振器与有效载荷组成。应用Rongong修正的模态应变能方法计算的相关参数与结果见表2。从表2中可以看出，隔振器在阻尼材料与阻尼结构设计方面的改进发挥了显著作用，等效阻尼比达到 0.294，可有效抑制共振。同时，所设计的隔振器等效阻尼比值正好具有最佳的衰减冲击的效果［9，15］。

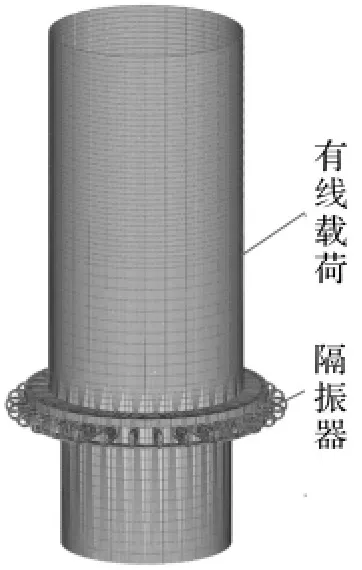
图12 隔振系统有限元模型Fig.12 FEM of vibration isolation system

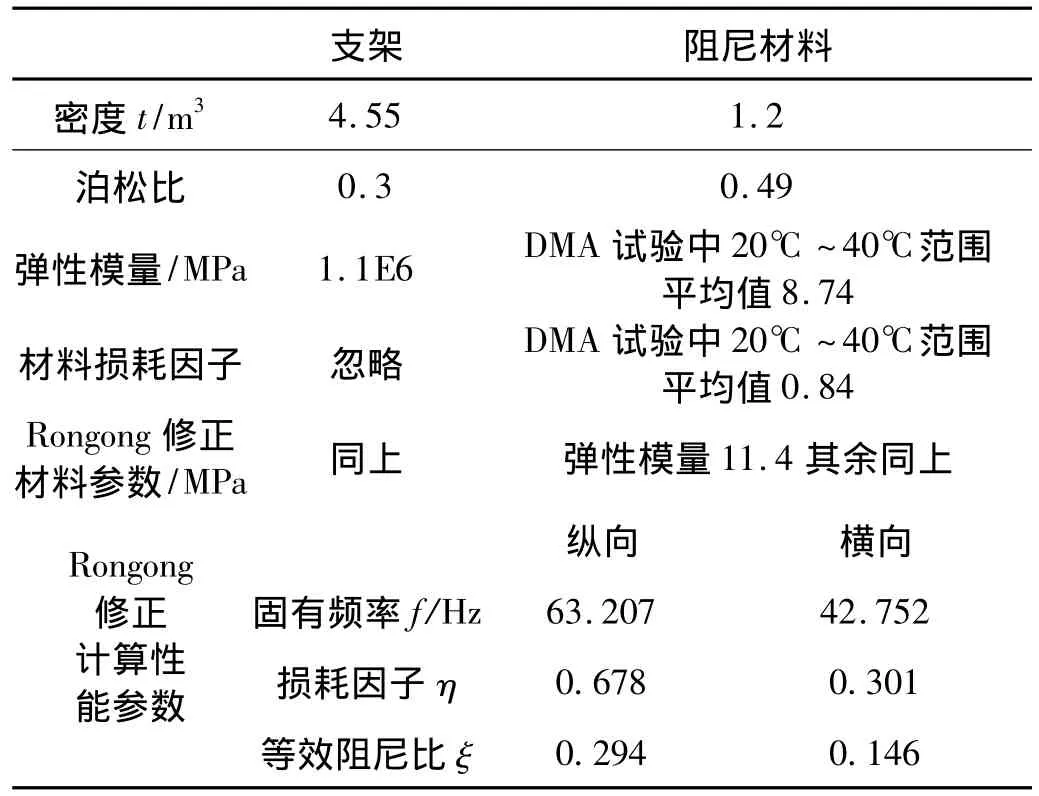
表2 隔振系统仿真分析参数及结果Tab.2 Performance parameters of isolator by simulation

4 隔振系统试验

根据航天载荷质量及隔振器额定载荷，隔振系统由30个隔振器组成，均匀圆周布局。为进行隔振系统试验，设计了在质量、重心、尺寸、惯性矩方面相似的试验模型代替真实载荷。隔振器上部接试验模型的法兰，下部接工装底座，工装底座固联于振动台上。试验设备为702所30 t推力振动试验系统。试验系统组成见图13，传感器测点布局见图14，x与y轴均为横向，z轴为纵向。传感器共设计7个测点，每个测点安装三个方向的加速度传感器。总共21个测量通道除了检测隔振器的直接输入输出外，还有考察测量一致性，检测远离质心振动的作用。正弦振动与随机振动试验条件见表3。

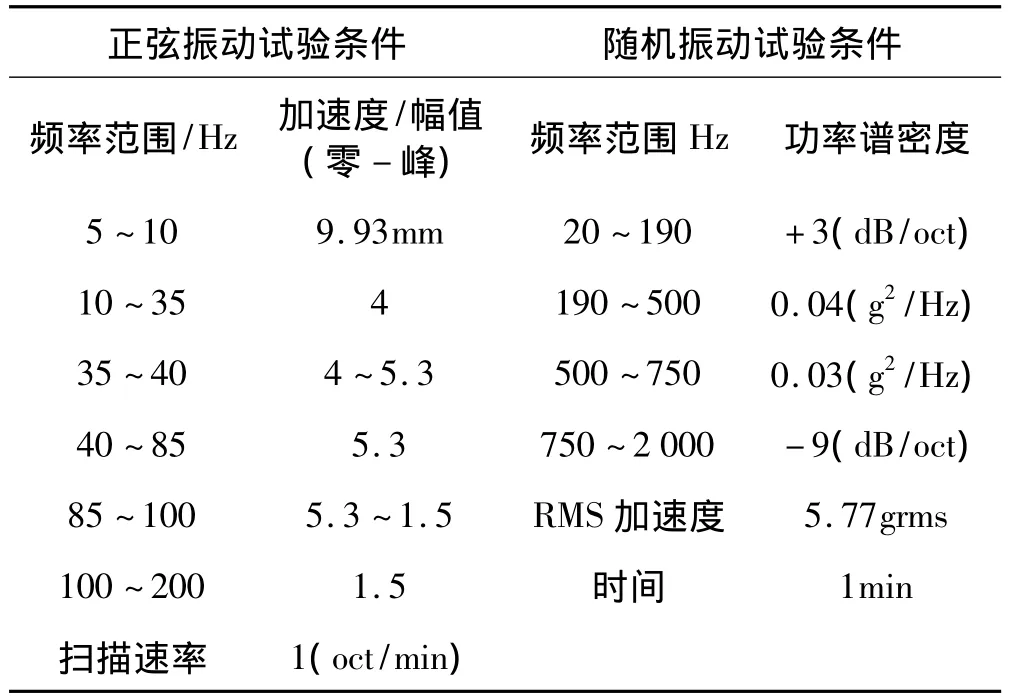
表3 隔振系统正弦与随机振动试验条件Tab.3 Sinusoidal and random experimental conditions for vibration isolation system

简明起见，下文正弦与随机试验结果均指4号测点的响应，代表隔振器最直接的性能。隔振系统正弦振动与随机振动试验结果见图15～图18。隔振系统性能参数见表4，可见，隔振系统具有相当高的等效阻尼比，实现了中低频有效抑制共振，宽频范围内有效衰减加速度RMS值的目标。同时，从表4中还可以看出，纵向试验结果与仿真分析结果相当接近，误差约在10%以内。

图13 试验系统组成Fig.13 Experiment configuration of vibration isolation system

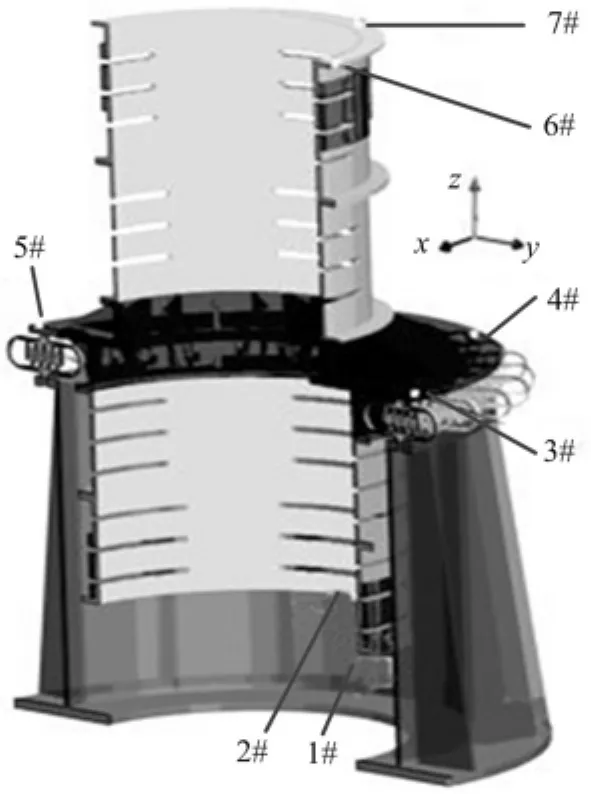
图14 传感器测点布局Fig.14 Sensors layout for vibration isolation system

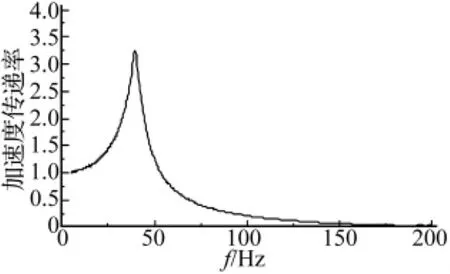
图15 横向正弦扫频试验曲线Fig.15 Sinusoidal response of horizontal experiment

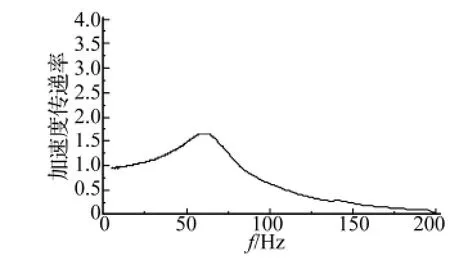
图16 纵向正弦扫频试验曲线Fig.16 Sinusoidal response of vertical experiment

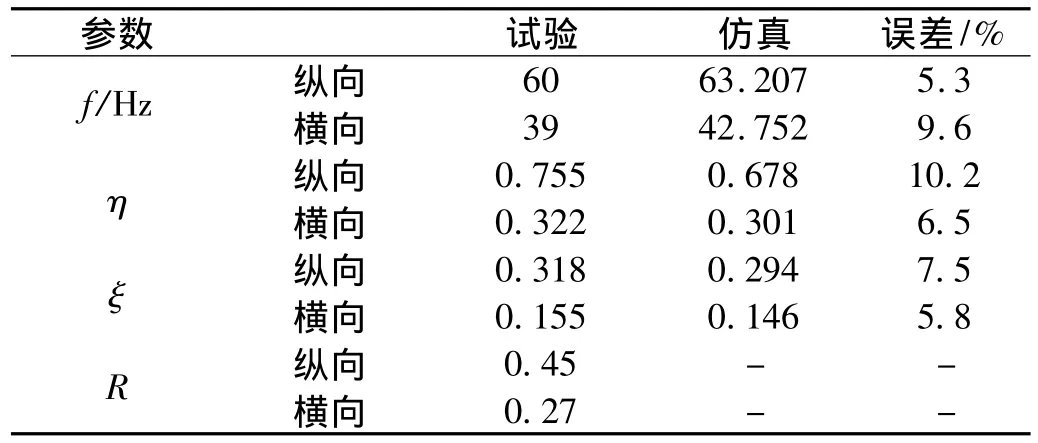
表4 隔振系统试验性能参数Tab.4 Performance parameters of vibration isolation system

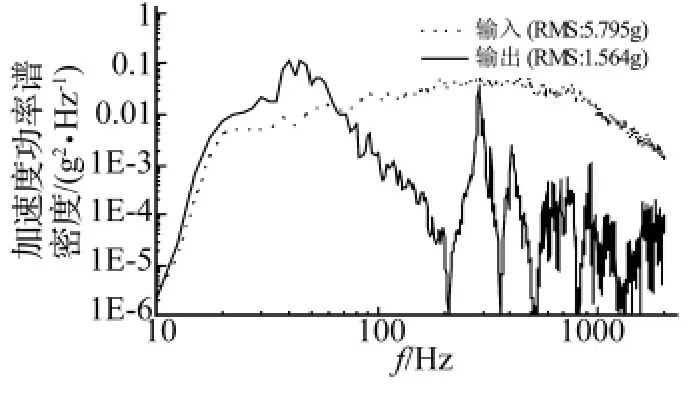
图17 横向随机振动试验曲线Fig.17 Random response of horizontal experiment

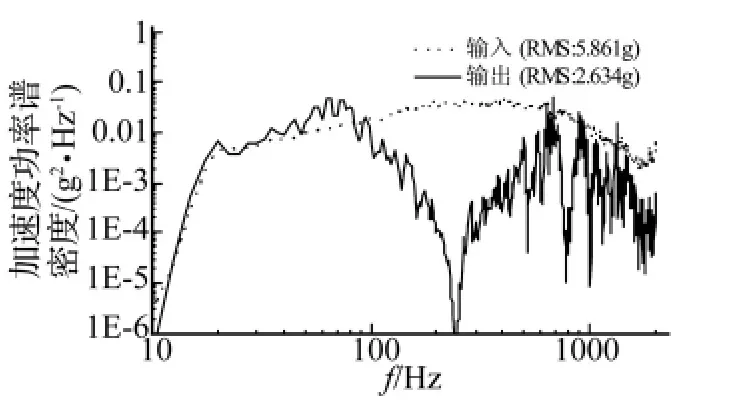
图18 纵向随机振动试验曲线Fig.18 Random response of vertical experiment

表中，R为加速度RMS输出与输入的比率;其余符号含义同表2。

5 结论

(1)针对某航天载荷，设计出一种新型的具有近等强度、高阻尼、兼顾冲击保护、阻尼材料粘结牢固等特点的航天载荷隔振器;

(2)在隔振器支架的设计中，由引入了等强度理论，设计了变厚度隔振器支架，对比分析表明，在基本不改变质量，体积，刚度的前提下安全系数提高了0.4倍;

(3)在隔振器阻尼材料的设计中，应用阻尼材料能量耗散理论及Rongong修正模态应变能方法设计了新颖的梳状剪切型阻尼结构，使隔振器具有高等效阻尼比;

(4)所设计的隔振器等效阻尼比具有良好的冲击衰减性能;

(5)由30个隔振器组成的隔振系统的正弦扫频与随机振动试验验证了隔振器能有效抑制中低频共振(等效阻尼比:纵向0.318，横向0.155)与衰减宽频带上随机振动(加速度RMS输出与输入的比率:纵向0.45，横向 0.27)。

［1］ Liu L K，Zheng G T.Parameter analysis of PAF for wholespacecraft vibration isolation［J］.Aerospace Science and Technology，2007，11(6):464 －472.

［2］马兴瑞，于登云，韩增尧，等.星箭力学环境分析与试验技术研究进展［J］.宇航学报，2006，3:323－331.

［3］ Chen Y，Fang B，Yang T，et al.Study of whole-spacecraft vibration isolators based on reliability method［J］.Chinese Journal of Aeronautics，2009，22(2):153 －159.

［4］王跃宇，冷力强，李 志，等.星箭适配器(PAF)隔振技术的进展［J］.航天器环境工程，2007，1:43－46.

［5］张 军，谌 勇，骆 剑，等.整星隔振技术的研究现状和发展［J］.航空学报，2005，2:179－183.

［6］Wilke P S，Johnson C D.Recent launches using the SoftRide whole-spacecraft vibration isolation system［A］.The AIAA Space Conference［C］.Albuquerque，USA，2001:4708－4717.

［7］张 军，谌 勇，张志谊，等.一种整星隔振器的研制［J］.振动与冲击，2005，24(5):35－38.

［8］夏益霖，吴家驹.航天发射的低频振动环境及其模拟［J］.强度与环境，1998，1:1 －8.

［9］屈维德.机械振动手册［M］.北京:机械工业出版，1992.

［10］张少实.新编材料力学(第2版)［M］.北京:机械工业出版社，2010.

［11］闻邦椿.振动机械理论、技术及其应用［M］.北京:科学出版社，2010.

［12］刘棣华.粘弹阻尼减振降噪应用技术［M］.北京:宇航出版社，1990.

［13］Torvik P J，Runyon B.Modifications to the method of modal strain energy for improved estimates of loss factors for damped structures［J］.Shock and Vibration，2007，14(5):339－353.

［14］ Rongong J A.Reducing vibration levels using‘Smart Joint’concepts［A］.Proceedings of IMSA 25，Noise and Vibration Engineering［C］.Leuven，Belgium，2000:817 －824.

［15］辛 勇，何成宏，杨国泰.冲击机械隔振中阻尼的应用研究［J］.振动与冲击，1999，18(2):45－49.