国际干散货远期运费市场套期保值效率研究＊

朱意秋 任仙玲 吕令颖

（中国海洋大学经济学院，山东青岛266100）

国际干散货远期运费市场套期保值效率研究＊

朱意秋 任仙玲 吕令颖

（中国海洋大学经济学院，山东青岛266100）

本文用四种模型计算了四条国际干散货航线的远期运费套期保值比率并对其效率进行比较。样本内OLS效率最高，样本外时变G－DVEC效率最高，样本内外向量自回归模型的效率均居中。与中国铁矿石进口运输相关的C3和C5航线的套保效率比较高，样本内可以达到60%，样本外可以达到30%，既高于传统航线C4和CTC，也高于我国某些商品期货市场的套保效率。本研究认为，G－DVEC模型可以有效规避航运现货市场的价格波动风险，而OLS模型不宜用于套期保值操作。

FFA；套保比率；套保效率

一、引言

国际干散货运输通常是不定期船，受运力供求、金融市场波动，甚至中国经济形势等众多因素的影响，干散货运输费率极不稳定，且变动幅度很大。为规避运价波动的风险，国际航运界先后创设过多种运费衍生工具，远期运费协议（Forward Freight A－greements，简称FFA）是1992年在伦敦创设且至今最为活跃的一种。协议由当事人双方直接或者在经纪人撮合下成交，协议中规定具体的船型、航线、合约价格、数量和到期月等，规定在到期月月底收取或支付结算价格与合约价格的差额①具体地说，程租航线由每月最后七个交易日的平均价构成，期租船由每月所有交易日的平均价构成。。根据伦敦波罗的海航运交易所的市场报告，FFA交易品种包括表1所示的四种船型的10条航线，每条航线的远期运费又分当月、未来几个月、几个季度和数个年份等十几种。

表1 国际干散货FFA交易的主要航线

C3和C5是我国进口铁矿石最重要的两条运输航线，2006年以来经历了剧烈的价格波动。以C5航线为例，2008年6月飙升到50.85美元/吨，至12月又骤跌至3.87美元/吨，半年内价格剧降93%，给我国钢铁和航运业带来巨大经营风险。有些相关企业尝试通过FFA市场的套期保值操作降低实体运输市场的价格风险，但在对冲相应即期市场敞口风险的远期数量上并没有自觉意识。因此，研究FFA市场最佳的套期保值比率及其效果具有重要的实用价值。

国内外对FFA市场的套期保值功能及其操作有较多的论述性文章，但是在金融时间序列方面的实证文章不是很多。2004年Kavussanos等在伊兹密尔第14届国际海运经济协会年会上发表的“柜台交易的远期运费市场套期效率”一文研究的船型是巴拿马型船，［1］数据区间从1997年至2002年，其主要结论是：FFA在各条航线上的套期效率有较大差异，跨大西洋航线的套期效率比较理想，而跨太平洋航线的套期效率差一些，其原因是前者为比较成熟且稳定的运输市场，而跨太平洋航线是一个发展迅速且不太成熟的市场。他们还认为，相比于其他金融和商品期货市场，FFA的套期保值效率不太理想。沈吴诚等对FFA市场的套期保值比率及其有效性进行了研究，［2］航线为P2A、P3A、PT/C和CT/C，数据区间为2005年至2009年，其主要结论是：P2A和P3A的套保绩效最好，而交易最为活跃的CT/C和PT/C的套期保值绩效比较差。上海交通大学的朱剑和大连海事大学的肖贻铭分别在其研究生论文中研究了FFA市场的套期保值效率问题。

综上所述，国内外关于FFA市场的实证研究均未对我国铁矿石进口运输航线C3和C5进行过研究，本文将填补这个空白，作为C3和C5航线的对照，本文还选取了FFA交易中受到追捧的C4和CTC航线一并研究。所有航线的数据区间从2006年1月至2011年3月（分为样本内和样本外两段），数据类型为即期和一个月远期，套期保值比率的计算模型分为静态和动态两类。

二、最优套期保值计算模型

套期保值是指以回避现货价格风险为目的的期货交易行为。具体到航运市场，是指在实体租船市场租入或租出船舶的同时，在远期市场上买入或者卖出合约，以一个市场的盈利弥补另一个市场的亏损，从而达到规避价格波动风险的目的。套期保值比率是持有远期合约的数量与风险暴露资产数量之间的比率，或者说，对应于1单位的现货应该对冲的远期数量。本文将以现货和远期组合资产价格波动风险最低为目标函数，设h＊为最小方差最优套期保值比率，各种计算套期保值比率的模型如下：

（一）以OLS模型估计h＊

Ederington证明最小方差最优套期保值比率可以通过现货和期货差分序列的回归方程来进行估计。［3］在近年实证研究中，鉴于收益率序列的良好统计特性，人们更多地使用收益率序列作为最优套期保值比率的变量，本文也是如此。按照Ederington的观点，套保比率h＊正是式（1）中的回归系数β。

式中，Rst和Rft分别为现货和远期的收益率序列。

（二）以B－VAR模型估计h＊

Myers等指出，利用OLS模型估计最优套期保值比率，其回归残差具有序列相关性，而且OLS模型未能考虑历史上期货和现货价格变动对当前价格变动所产生的影响。［4］因而提出以双变量向量自回归模型（B－VAR）估计套保比率的方法，其数学表达式如下：

p表示最优滞后阶数，α、β、η和θ分别表示各变量回归系数，h＊通过式（4）求得：

式中，σsf和σff分别为通过公式（2）和（3）所求得的即期与远期协方差和远期方差。

（三）以B－VEC模型估计h＊

B－VAR模型虽然解决了OLS模型中的残差自相关问题，却依然忽略了期货与现货价格之间存在的协整关系可能对套期保值比率估计所产生的影响。Ghosh根据Granger和Engle的协整理论，［5］提出用双变量误差修正模型（B－VEC）估计套期保值比率的方法，Ghosh和Lien的研究表明，［6］如果忽略期货和现货价格之间存在的协整关系，将会得到一个偏小的最优套期保值比率。B－VEC的表达式为：

式中，误差修正项ect（－1）的表达式详见表4，k为调整系数，用以反映市场对于长期均衡的偏离会以多快的速度做出反应。利用B－VEC模型估计最优套期保值比率h＊的计算公式与（4）式相同。

以上三种模型所获得的最优套期保值比率均为常数，不随时间而改变，因而被称为静态套期保值比率。

（四）以G－DVEC模型估计h＊

实际上，金融时间序列通常存在显著的波动聚集性，基于方差为常数的假定必然会对最优套期保值比率的估计造成不利影响，提出了动态（或时变）套期保值的概念，运用多元GARCH模型的方差和协方差序列估计套期保值比率。但是，估算多元GARCH模型的矩阵元素是比较困难的，Bollerslev等将一元指数加权滑动平均GARCH推广到多元GARCH模型，并将其矩阵做了对角对称后得到的简化模型，称为G－DVEC模型。［7］

式中，m和s是非负整数，Ai和Bj是对称矩阵，表示矩阵相应元素相乘，a和a′为残差序列向量。具体到即期和远期的二元DVEC（1，1）模型中，其下三角所表示的即期条件方差方程、即期与远期协方差方程和远期条件方差方程的展开式如下：

式中，εs和εf分别为即期和远期均值方程残差序列，σsf、σff均为随时间而变化的序列，由此得到的套期保值比率h＊也是随时间变化的序列。

三、套期保值效率比较模型

套期保值效率是指进行套期保值操作比没有套期保值操作时收益率波动减少的百分比。根据Kroner和Sultan关于套保效率的衡量方法，设：Var（Rs）为现货市场上没有进行套期保值的方差，Var（H）为操作套期保值后组合资产的方差，见式（11），τ为套期保值的效率，见式（12）。［8］τ值越大说明保值效率越高。

运行Eviews 6，第一步，根据保值比率模型所得的h＊、即期和远期收益率序列，构造资产组合序列H，记算其标准差和方差；第二步，计算即期收益率序列的标准差和方差；第三步，根据式（12）计算τ值，即为实施套期保值措施后收益率波动减少的程度或百分比。

四、数据及其检验

（一）数据来源及检验

本文实证研究中使用的即期和远期价格数据均来自波罗的海航运交易所，远期数据只选取了1个月远期，样本内区间为2006年1月3日至2010年11月30日，除掉没有交易和不合要求的日期后，C3、C4、C5和CTC各获得1100天以上的有效观测值，见图1。

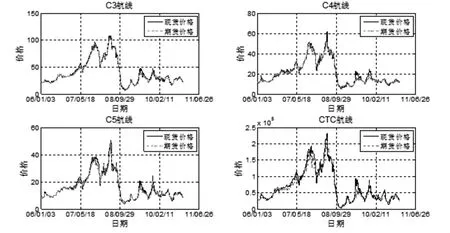
图1 各航线即期和远期价格走势图

（二）数据的描述性统计

对原始价格数据先取对数，再差分，获得了日收益率序列，RS为即期收益率，RF为远期收益率，各航线即期和远期收益率的统计性描述如表2所示。

表2 各航线即期和远期日收益率统计性描述

从表2中可以看出，5年间除了C3航线外，其他三条航线的远期市场平均是亏损的。日收益率的最大值和最小值均出现在CTC航线远期，说明该航线的远期市场比较活跃也充满了风险。各航线各期的偏度大部分为正值，峰度显著大于正态分布的3，说明大部分序列具有尖峰厚尾分布特征，符合一般金融时间序列的情况。

（三）数据检验

1、ADF平稳性检验

运用增广Dick－Fuller（ADF）检验，对原始价格序列、对数序列，以及收益率序列分别进行了平稳性检验。检验说明，各航线各期的价格序列（S和F）和对数序列（LNS和LNF）都是非平稳序列，但各个收益率序列（RS和RF）无论在l%、5%，还是10%的显著性水平下其ADF统计值显著小于各水平下的临界值。因此，收益率序列是平稳的，那么，对数序列是一阶单整序列，符合协整的前提条件。

表3 各序列水平下ADF检验的t统计量

2、协整检验

将各航线成对的对数序列进行JOHANSON协整检验，其原假设为两个序列不存在协整关系，如果迹统计值大于临界值，则否定原假设。表4中列出了协整检验的迹统计值和协整方程个数，并将标准化协整方程列在第4列，该式也是B－VEC模型中误差修正项的表达式。

表4 JOHANSON协整检验及其方程

五、套期保值比率及其检验

本文实证研究的目的有三个：第一，比较各种模型下套期保值比率和效率的差别；第二，比较各个航线套期保值比率和效率的差别；第三，比较样本内和样本外套期保值比率和效率的差别。

（一）OLS下的h＊及其检验

首先用公式（1）计算OLS模型下的套期保值比率β（也是远期的回归系数）及其t检验值，如表5所示。

表5 OLS模型下最优套期保值比率的估计及其检验

从上表5中可以看出，在OLS模型下，各航线远期收益率的回归系数的t检验都是显著的，C5套期比率最高，达到0.969，CTC的比值最小，只有0.380。

为了检验如上回归模型是否满足OLS假设，我们对各个残差序列进行了滞后12阶的Q－统计自相关检验、White异方差检验和正态分布检验。检验结果表明，残差序列均存在高阶自相关，在5%的显著性水平下，均拒绝“不存在异方差”的原假设，各残差均呈现非正态分布。由此看来，表5所列的套保比率（即回归系数）应该是不可靠的。

（二）B－VAR和B－VEC模型下的h＊

为求得双变量自回归模型下的方差和协方差值，运用eviews 6软件做了如下操作：

1、输入各航线即期和远期收益率序列，运行VAR模型，分别记录远期均值方程的方差σff和两者的协方差σsf，代入公式（4）中，计算最小方差最优套期保值比率，见表6。

2、输入各航线即期和远期对数序列，运行VEC模型，得到带有协整方程的对数差分序列（即收益率）的双向量均值方程，与VAR模型的操作一样，可以得到VEC模型下的最优套保比率，见表6。

表6 最优套期保值比率估计

（三）G－DVEC模型下的h＊

将成对的即期和远期收益率序列以system的方式打开，根据各序列的自相关阶数，确定回归变量个数②经测试，所有航线的远期序列自相关阶数皆为1，即期序列的自相关阶数除了C4外皆为2（C4的即期自相关阶数为1）。。在ARCH模型中选择diagonal VECH模型，记录均值方程中各回归变量的系数和残差序列，记录波动方程中各矩阵系数、协方差序列和远期方差序列，运用公式（4）获得G－DVEC模型下的最优套期保值比率，如图2所示。表6第5行为时变套保比率的均值。

图2 动态套期保值比率走势

从表6可以看出，相同模型下C3和C5的套保比率显著大于C4和CTC的数值，而且经常是CTC的两倍以上，譬如，在B－VAR模型下，C3为0.708，CTC为0.280。同一航线下，OLS所计算的比率最高，而G－DVEC模型下的比率最小，B－VAR和BVEC的计算结果相近，与Lien的研究结果一样，［7］带误差修正项的B－VEC所算出的最优套期保值比率要大于B－VAR的。

在表6中，各模型各航线所列的最优套期保值比率均小于1，异于套保比率恒为1的“幼稚”套保策略，说明在规避航运现货风险而套期保值时，需要套保的远期数量小于现货的。当然，买卖远期合约的数量越小其交易成本越低。

六、套期保值效率比较

本文以2010年11月底为界，将数据分为样本内和样本外两段，分别评估其套保效率。

（一）样本内套期保值效率比较

以2006年1月至2010年11月的数据计算各航线各模型下的套期保值效率，如表7所示。

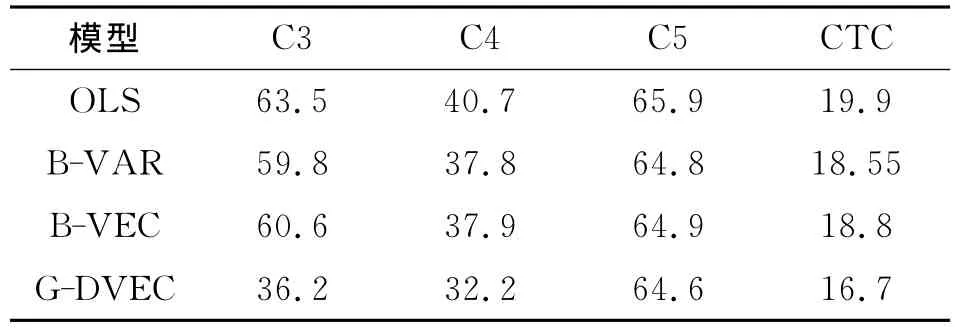
表7 样本内套期保值效率τ（%）

从表7中可以看出，不管什么模型，都是C5航线的保值效果最好，大约在65%，C3次之，C4再次之，而CTC最低，风险降低程度不到20%。实际上，FFA交易中，CTC的交易量大于C4，而C3和C5的交易量要小于C4。如此说来，与我国铁矿石运输相关的C3和C5航线保值效果比其他传统航线好很多，个中原因要么是市场效率高，要么是这两条航线的远期数据更多是专家估计的结果③作者特意为了C3和C5远期数据的确定方法询问过波罗的海航交所，其答复是，某天某航线如果有远期交易数据，根据这些数据算一个平均值公布，如果没有交易数据则由航交所的专业委员会专家根据某种规则给出一个估计值再公布。但是这个估计规则是保密的。。在同一航线下，OLS模型的保值效率最好，动态保值的最差，B－VAR和B－VEC两模型结果相近，效率居中。

（二）样本外套期保值效率比较

为了比较样本外距样本内时间长度对套期保值效率的影响，我们做了2期样本外计算，第一期只有2010年12月的数据，第二期从2010年12月初到2011年3月底，各期样本数见表8第2行。

表8 样本外套期保值效率τ（%）

在OLS、B－VAR和B－VEC模型下将表4所估算的最优保值比率代入式（11）中，得到套期保值组合序列的标准差，算成方差，再运用公式（12）计算套保效率。G－DVEC模型下样本外套保效率的计算比较复杂，在eviews软件中的操作如下：

（1）承接样本内回归系数，计算样本外真实值和估算值之间的估计误差；（2）承接样本内波动方程矩阵系数，并用上一步所得的估计误差，按式（9）和式（10）计算协方差和远期方差序列，计算套保比率序列；④为了承接样本内的协方差和方差值，样本外数据需要与样本内数据有一定的重叠，即样本内的最后三天（自相关全部是一阶时）或4天（自相关至少有一个是二阶时）的数据放到样本外数据的最前面。（3）根据式（11）计算组合资产序列的方差，计算现货序列的方差，按式（12）计算保值效率。

从表8中可以看出，样本外套保效率均比样本内的差，最佳状况也只能改善40%，最差的竟然出现了负值，此时套期操作还不如不做的好。就不同模型而言，各航线在G－DVEC下的保值效率最高（C3航线除外），OLS的效率最差，B－VAR和BVEC下的效率居中。样本外第一期的保值效率比第二期的保值效率好许多。可以推测，样本外时间越长，套保效率越差。

七、结论

利用OLS、B－VAR、B－VEC和G－DVEC四种模型均可以有效计算出各航线的套保比率和套保效率。就样本内套保效率而言，OLS下效率最高，GDVEC效率最差，B－VAR、B－VEC居中，而样本外套保效率的比较正好相反，G－DVEC最好，OLS最差，B－VAR和B－VEC依然居中。本文认为，利用历史数据计算最优套保比率，不是为了回顾过去，而是用于指导未来远期市场的套期操作。所以，样本外的效率更有实际价值。本文先是验证了OLS回归系数的无效，又在样本外套保效率比较中获得了支持，因此，OLS模型不适宜指导未来套期保值市场的操作。本文推荐套保实践中使用动态时变G－DVEC模型估计最优套期比率，并且建议样本内数据不断推进，经常更新估计参数，以确保样本外时变的套保比率保持“新鲜”。

C3和C5航线不管在样本内还是样本外其套保效率均好于传统的C4和CTC航线，样本内的套保效率约为60%，样本外采用动态模型的话约为30%。套保效率多高即可满足避险需求，尚未见有文献讨论。可以比较的是，在彭红枫，胡聪慧关于我国大豆期货保值效率研究中，样本内保值效率约为15%，样本外保值效率约为8%，认为风险明显降低。［9］肖树强，赵息研究我国钢材期货套保效率时样本内的效率也仅在3～15%之间。［10］由此可说，对我国两条重要的铁矿石运输航线进行套期保值操作其效果是比较理想的。

［1］Kavussanos M.G，Visvikis I.D.The hedging performance of over－the－counter forward shipping freight markets.Conference Proceedings，14th International Association of Maritime Economists（IAME）Conference，Izmir，30June–2July 2004.

［2］沈吴诚，王小明，曾秋根.干散货远期运费协议的套期保值有效性研究［J］.会计之友，2010，（5）：63－66.

［3］Ederington，L.H..The Hedging Performance of the New Futures Markets［J］.Journal of Finance，1979（34）：157－170.

［4］Myers R..J，Thompson S R.Generalized optimal hedge ratio estimation［J］.American Journal of Agricultural Economics，1989（71）：858－867.

［5］Ghosh A.Hedging with stock index futures：estimation and forecasting with error correction model［J］.The Journal of Futures Markets，1993（13）：743－752.

［6］Lien.The effect of the cointegration relationship on futures hedging：a note［J］.Journal of Futures Markets，1996（16）：773－780.

［7］Bollerslev，T.，Engle，R.F.，and Wooldridge，J，M..A capital－asset pricing model with time－vary corariance.Journal of Political Economy，1998（96）：116－131.

［8］Kroner K.F，Sultan J.Time－varying distributions and dynamic hedging with foreign currency futures.Journal of Financial and Quantitative Analysis，1993（28）：535－551.

［9］彭红枫，胡聪慧.中国大豆期货市场最优套期保值比率的实证研究［J］.技术经济，2009，（1）：62－66.

［10］肖树强，赵息.我国钢材期货套期保值比率与绩效实证研究［J］.价格理论与实践，2010，（7）：48－49.

Abstract：This paper estimates hedging ratios of forward freight on 4international dry lines by means of 4models，and compares their performance.The performance under model OLS is the highest by in－samples，where as model time－varying G－DVEC is the best by out－samples，and Vector Autoregressive model in the middle by both in and out－samples.C3 ＆C5，relating China＇s importing iron ore transport，have good hedging performance，reaching 60%by in－samples and 30%by out－samples，which are better than other two classic lines C4＆CTC and some Chinese commodity future markets as well.This study indicates that by means of G－DVEC should avoids price risk of shipping spot market effectively，but OLS is not suitable for hedging operations.

Key words：FFA；hedging ratio；hedging performance

责任编辑：王明舜

Study on Hedging Performance of International Dry Forward Freight

Zhu Yiqiu，Ren Xianling，Lv Lingying
（School of Economics，Ocean University of China，Qingdao 266100，China）

F224；F830.9

A

1672－335X（2012）02－0055－07

2012－02－28

国家社会科学基金项目“FFA在中国相关航线上的市场效率研究”（09BJY074），国家自然科学基金项目“Copula分位数协整理论及其在FFA市场的应用研究”（71101134）

朱意秋（1957－ ），女，山东青岛人，中国海洋大学经济学院教授，主要从事海运经济研究。