关于四元射影空间中的全实伪脐子流形

操江涛，汪兴上

（1.安徽师范大学数学计算机科学学院，安徽芜湖241000；2.安徽中医药高等专科学校学生处，安徽芜湖241000）

关于四元射影空间中的全实伪脐子流形

操江涛1，2，汪兴上1

（1.安徽师范大学数学计算机科学学院，安徽芜湖241000；2.安徽中医药高等专科学校学生处，安徽芜湖241000）

研究了四元射影空间QPnc中全实伪脐子流形问题，利用活动标架法获得了这类子流形推广的Simons型积分不等式及成为全测地子流形的刚性定理.

四元射影空间；伪脐子流形；全测地子流形

0 引 言

四元射影空间QPnc是四元截面曲率c＞0的空间形式，V是它的四元结构，M是等距浸入到QPnc的m维黎曼流形.笔者用Ts（M）和T⊥s（M）分别表示M在x点的切空间和法空间，x∈M；如果对于任意的φ∈V和任意的x∈M，均有φTs（M）⊂T⊥s（M），则称M是QPnc的全实子流形.

Shen Yibing和瞿成勤在文［1－2］中讨论了四元射影空间QPnc中的全实极小子流形.B.Y.Chen和C.S.Houh在文［3］中讨论了四元射影空间QPnc中的全实子流形.对于复射影空间中的全实伪脐子流形，已经有许多结果［4－5］.笔者将外围空间推广到四元射影空间，利用活动标架法对四元射影空间QPnc中全实伪脐子流形进行了研究，得到如下定理：

定理1 设Mn是四元射影空间QPnc中n维紧致全实伪脐紧致子流形，S为Mn的第二基本形式模长的平方，则有如下积分不等式：

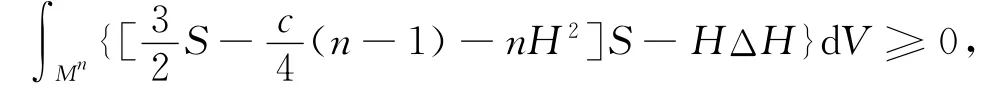
其中QPnc是具有四元截面曲率c＞0的4n维四元射影空间.

定理2 设Mn是四元射影空间QPnc中n维具有平行平均曲率向量紧致全实子流形，S为Mn的第二基本形式模长的平方，则有如下积分不等式：

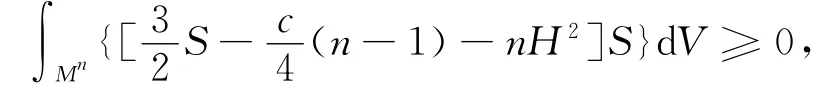
其中QPnc是具有四元截面曲率c＞0的4n维四元射影空间.

注 因为Mn是QPnc中具有平行平均曲率向量全实子流形，则平均曲率H＝C为常数.由此得如下推论：

推论1 设Mn是具有全纯截面曲率c的四元射影空间QPnc中具有平行平均曲率向量紧致全实子流形，若其第二基本形式模长的平方S满足则Mn为全实全测地子流形.

1 预备知识

设N是4n维的四元Kaehler流形，其殆四元数结构I，J，K满足

其中Id表示（1，1）型张量场.本文约定各类指标的取值范围如下：

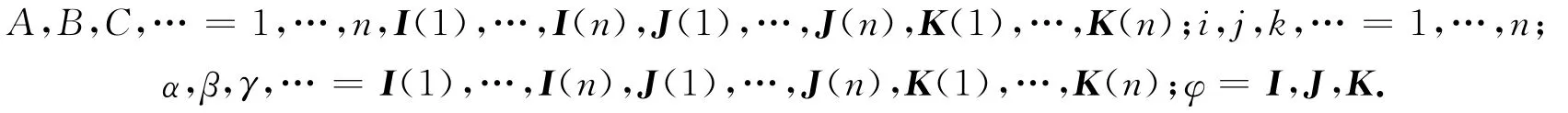
并且不特别说明∑号是对重复指标在相应范围内的求和.选取QPnc中的局部正交标架场e1，…，en，eI（1）＝Ie1，…，eI（n）＝Ien，eJ（1）＝Je1，…，eJ（n）＝Jen，eK（1）＝Ke1，…，eK（n）＝Ken，使得限制到Mn上时｛ei｝与Mn相切.在此标架下，I，J，K有如下形式：

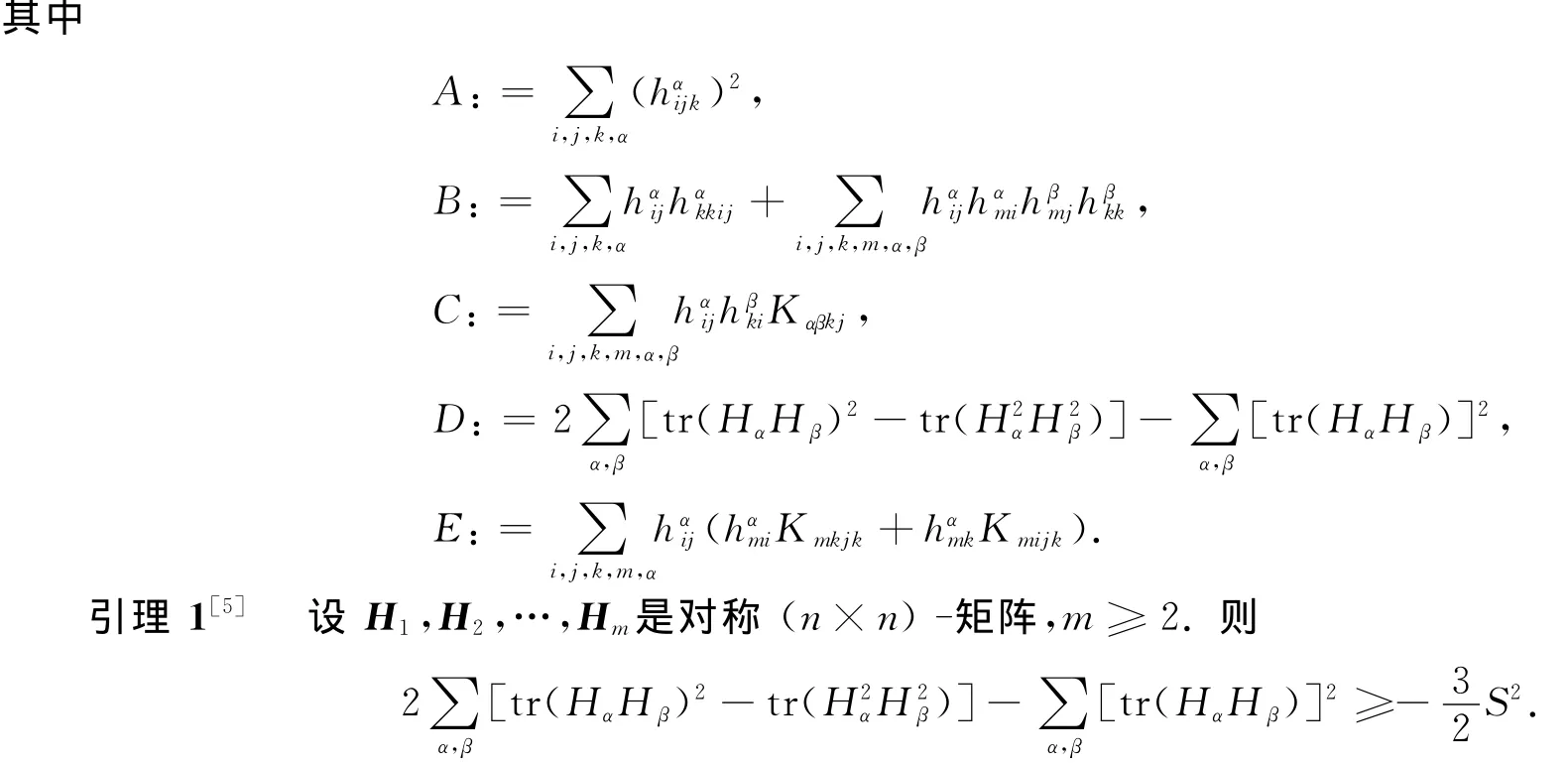
2 定理的证明

以下假设Mn是四元数射影空间QPnc中的伪脐全实子流形.

定理1的证明 显然

参考文献：

［1］Shen Yibing.Totally real minimal submanifolds in a quaternionic projective space［J］.Chin Ann Math，1993，14B（3）：297－306.

［2］瞿成勤.四元数射影空间QPnc中全实极小子流形［J］.工程数学学报，1997，14（2）：32－38.

［3］Chen B Y，Hough C S.Totally real submanifolds of quaternionic projective space［J］.Anna Math Pura ed Appl，1979，120（1）：185－199.

［4］Zhang Liang.On Totally real pseudo－umbilical submanifolds in a complex projective space［J］.Journal of Mathematical Research and Exposition，2008，28（2）：421－428.

［5］Liu Min，Song Weidong.On Complete totally real Pseudo－umbilical submanifolds in a complex projective space［J］.Journal of Mathematical Research and Exposition，2011，31（5）：946－950.

On Totally Real Pseudo－Umibilical Submanifolds in a Quaternionic Projective Space

CAO Jiang－tao1，2，WANG Xing－shang1
（1.School of Mathematics and Computer Science，Anhui Normal University，Wuhu 241000，China；2.Student Affairs Office，Anhui College of Traditional Chinese Medicine，Wuhu 241000，China）

This paper researched on the totally real pseudo－umibilical submanifolds in a quaternionic projective space，obtained a promotion of Simons'type integral inequality of compact submanifolds as well as the rigidity theorem to be the totally geodesic submanifolds by means of moving frames.

quaternionic projective space；pseudo－umibilical submanifolds；totally g eodesic submanifold

O186.16 MSC2010：53C20

A

1674－232X（2012）03－0237－04

10.3969／j.issn.1674－232X.2012.03.009

2011－11－17

安徽省高等学校优秀青年人才基金项目（2011SQRL021ZD）.

操江涛（1980—），男，硕士，主要从事微分几何研究.E－mail：wxshangsd＠163.com