Ⅰ-Ⅱ复合型裂缝应力强度因子和应变能释放率的关系
2012-09-06刘梦和王向东
刘梦和,王向东,邵 兵
(河海大学力学与材料学院,江苏 南京 210098)
断裂力学是以含裂缝构件为研究对象,分析在各种外界因素(荷载、腐蚀和温变等)作用下裂缝稳定扩展或失稳扩展的规律,研究含裂缝构件安全性的学科[1]。目前在线弹性范围内,对裂缝的安全性评估主要采用应力强度因子K和应变能释放率G两个物理量。
实际工程中,评价大坝等结构中裂缝的安全性时,K及其判据[2-3]广泛应用于裂缝的稳定性分析。邓爱民等[4]对混凝土进行拉剪断裂试验,得到了考虑断裂过程区的Ⅰ-Ⅱ复合型裂缝的断裂K判据。近十几年来,饶秋华等[5-8]一直着力于研究混凝土和岩石等多种材料的断裂参数,得到了它们的Ⅰ型、Ⅱ型和Ⅲ型裂缝的断裂韧度及相应的测试方法。
在线弹性断裂力学中,对单一型裂缝的K与G的关系已有完善的研究和相应的理论公式[9];对复合型裂缝的K与G的关系研究在国内外相关文献中很少见到。而在实际工程中,大部分裂缝都是复合型裂缝,仅将单一型裂缝的应变能释放率叠加得到复合型裂缝的G,不能很好地反映各单一型裂缝对复合型裂缝结果的影响。因此,有必要从理论上对复合型裂缝K和G的关系进行研究,并在此关系基础上建立复合型裂缝的断裂G判据,以此更好地评价工程结构中裂缝的稳定性。
Jones等[10-12]认为结构的复合型裂缝问题可简化为平面裂缝问题,有利于进行理论分析及有限元、边界元模拟分析。因此,本文采用平面板裂缝模型,从线弹性断裂力学理论的能量法入手,以单一型裂缝K与G的关系为基础,指导Ⅰ-Ⅱ复合型裂缝的K与G的关系,并应用有限元模拟计算对所得公式进行验证。
1 Ⅰ-Ⅱ复合型裂缝K与G关系公式的理论推导
Ⅰ-Ⅱ复合型裂缝的G,并不是将Ⅰ型和Ⅱ型裂缝的G简单叠加。Ⅰ-Ⅱ复合型裂缝的K与G的关系,可以按照裂缝闭合单位面积所做的功等于裂缝扩展单位面积所释放的能量的方法进行研究。
Ⅰ-Ⅱ复合型裂缝闭合单位面积所做的总功等于Ⅰ型和Ⅱ型裂缝闭合单位面积所做功的和。根据材料力学中功的互等原理,采用先加载正应力σ、再加载剪应力τ的方法计算总内力功ΔU,与采用先加载剪应力τ、再加载正应力σ的方法计算结果相同。本文采用第一种加载方式,如图1所示,假设原半长为a的裂缝,在正应力 σ的单独作用下,扩展微小长度Δa,扩展角为0°;在剪应力τ的单独作用下,扩展微小长度Δb,扩展角为 θ;在先加正应力σ、再加剪应力τ的作用下将扩展微小长度 Δc,扩展角为θ0。在线弹性情况下,Δa和Δb可合成为Δc。

图1 Ⅰ-Ⅱ复合型裂缝扩展方向
通过对Ⅰ-Ⅱ复合型裂缝的加荷载过程分析,在线弹性范围内,Ⅰ-Ⅱ复合型裂缝的总功ΔU的计算与加载顺序无关。因此可先分别计算正应力σ单独作用下裂缝扩展所做的功 ΔUⅠ及剪应力 τ单独作用下裂缝扩展所做的功ΔUⅡ,再计算Ⅰ型和Ⅱ型裂缝的应力场在Ⅱ型和Ⅰ型裂缝的位移场上所做的功ΔUⅠ,Ⅱ,三者的总和即为Ⅰ-Ⅱ复合型裂缝在正应力σ及剪应力τ共同作用下的总功ΔU。
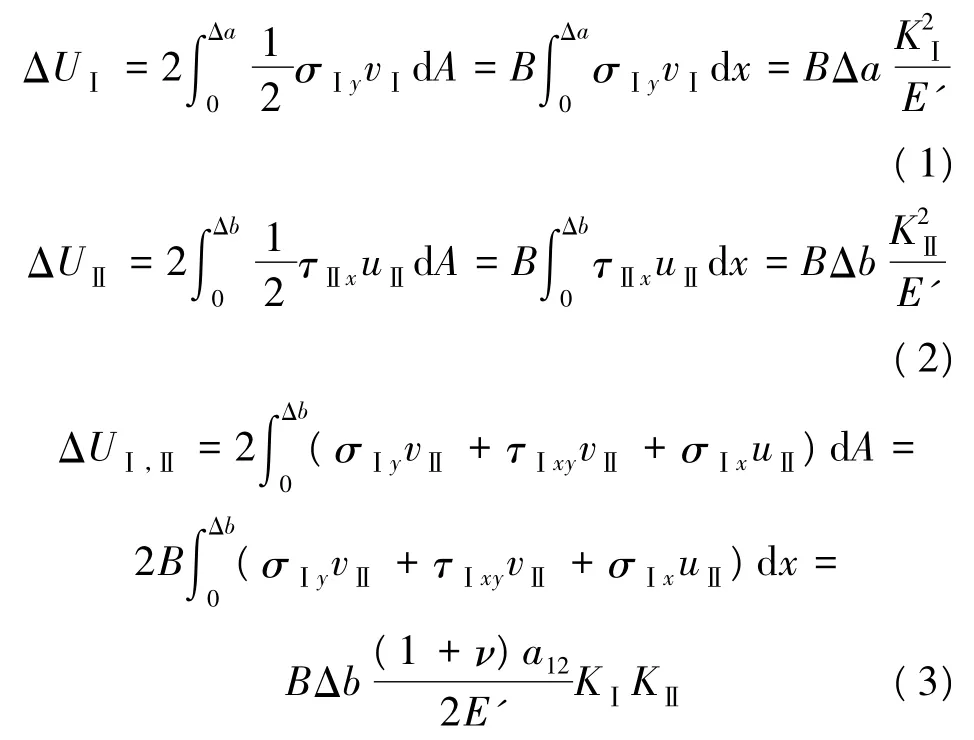
式中:B为板的厚度;u和v分别是x和y方向的位移分量;σx,σy,,τxy为应力分量;E′为弹性系数,平面应变状态时,E′=E/(1-ν2),平面应力状态时,E′=E,其中E为弹性模量,ν为泊松比;KⅠ和KⅡ分别为Ⅰ型和Ⅱ型裂缝的应力强度因子;a12为与泊松比ν有关的量。
Ⅰ-Ⅱ复合型裂缝扩展所做总功为

裂缝扩展面积ΔA=BΔc,由三角形正弦定理简化得Ⅰ-Ⅱ复合型裂缝的应变能释放率GⅠ-Ⅱ为

图2是KⅠ不同时,GⅠ-Ⅱ与KⅡ的关系。从图2中可以看出,KⅠ一定时,GⅠ-Ⅱ随着KⅡ的增大而增大,GⅠ-Ⅱ近似为KⅡ的二次函数。当KⅡ一定时,GⅠ-Ⅱ也随着KⅠ的增大而增大,GⅠ-Ⅱ也近似为KⅠ的二次函数。从式(5)可见,KⅠ和KⅡ这两个变量在公式中具有一定的对称性,即交换KⅠ和KⅡ的次序,并不影响其结果,这也能验证了G与加载次序无关的结论。

图2 不同 KⅠ时 GⅠ-Ⅱ与 KⅡ的关系
2 Ⅰ-Ⅱ复合型裂缝K与G关系公式的验证
2.1 公式的退化验证
根据最大应力准则,Ⅰ-Ⅱ复合型裂缝的扩展方向是沿周向应力最大的方向,由此可以计算出Ⅰ型和Ⅱ型裂缝的扩展角:Ⅰ型裂缝,KⅡ=0,扩展角 θ1=0°;Ⅱ型裂缝,KⅠ=0,扩展角 θ2=θ=-70.5°。由式(5)得到K与G的关系:
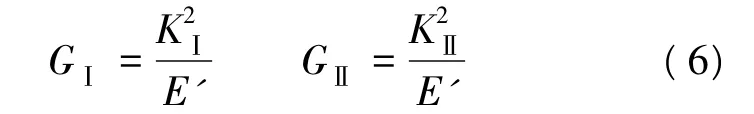
式(6)表明式(5)同样适用于单一型裂缝K与G的关系。
2.2 公式的有限元验证
以一带中裂缝的平板为研究对象,应用有限元分析软件Abaqus建立Ⅰ-Ⅱ复合型裂缝计算模型。荷载和约束情况如图3所示,板的底边x和y方向的位移均约束,在板的上表面加上正应力σ和切应力τ,两侧边加上切应力τ,σ=τ=2 MPa。图4为平板模型有限元网格,模型中裂缝的长度为平板宽度的1/14,半裂缝长a=2.3 cm,材料的弹性模量E=21 GPa,泊松比ν=0.3。图5为裂缝尖端周围区域网格的放大图,每个裂缝尖端附近都定义了16个奇异单元。=0.474 MPa·m1/2,KⅡ=0.427MPa·m1/2代入公式(5),计算得到Ⅰ-Ⅱ复合

图3 平板荷载及约束情况
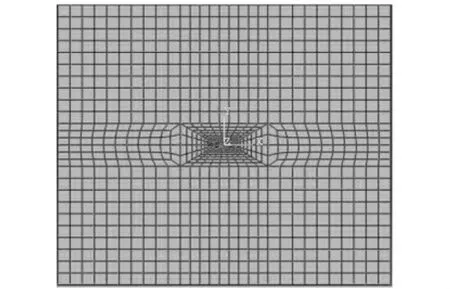
图4 平板模型有限元网格

图5 裂缝尖端周围有限元网格
将Abaqus建模计算所得KⅠ型裂缝的应变能释放率GⅠ-Ⅱ=19.9 N/m,有限元直接计算出的应变能释放率GⅠ-Ⅱ=19.4 N/m,二者的绝对误差为0.5N/m,相对误差为2.5%,小于5%,验证了所推导公式的合理性。
3 结论
a.通过线弹性断裂力学理论推导出Ⅰ-Ⅱ复合型裂缝K与G的关系公式,KⅠ和KⅡ这两个变量具有对称性;Ⅰ型和Ⅱ型裂缝产生的GⅠ和GⅡ在Ⅰ-Ⅱ复合型裂缝产生的GⅠ-Ⅱ中所占比例在公式中得以反映;此外Ⅰ型和Ⅱ型裂缝之间的相互作用产生的应变能释放率在GⅠ-Ⅱ公式中也有所体现。
b.Ⅰ-Ⅱ复合型裂缝K与G的关系式可以简化为单一型裂缝的K与G的关系式。
c.通过有限元计算得到的Ⅰ-Ⅱ复合型裂缝的应变能释放率与公式计算结果吻合较好,误差仅为2.5%,验证了推导公式的合理性。
:
[1]白二雷,许金余,姚焕忠,等.基于断裂力学的混凝土裂缝数值分析[J].空军工程大学学报:自然科学版,2004,5(2):81-84.
[2]李子阳,李季,向衍.基于三维 J积分的裂纹稳定性仿真计算[J].水利水电科技进展,2010,30(2):1-4.
[3]邵勇,王向东.基于断裂力学的高拱坝底缝稳定性分析[J].水电能源科学,2008,26(5):80-82.
[4]邓爱民,徐道远.混凝土Ⅰ-Ⅱ复合型拉剪断裂试验研究[J].河海大学学报:自然科学版,2010,38(4):428-432.
[5]RAO Qiuhua,SUN Z Q,STEPHANSSON O,et al.Shear fracture(mode Ⅱ)of brittle rock[J].International Journal of Rock Mechanics and Mining Sciences,2003,40(3):355-375.
[6]KHAN K,AI-SHAYEA N A.Effect of specimen geometry and testing method on mixed mode Ⅰ-Ⅱ fracture toughness of a limestone rock from Saudi Arabia[J].Rock Mechanics and Rock Engineering,2000,33(3):179-206.
[7]KRISHNAN G R,ZHAO X L,ZAMAN M,et al.Fracture toughness of a soft sandstone [J].International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts,1998,35(6):695-710.
[8]孙宗颀,饶秋华,王桂尧.剪切断裂韧度(KⅡC)确定的研究[J].岩石力学与工程学报,2002,21(2):199-203.
[9]王铎.断裂力学[M].哈尔滨:哈尔滨工业出版社,1989.
[10]JONES R,MOLENT L,PITT S.Study of multi-site damage of fuselage lap joints[J]. Theoretical and Applied Fracture Mechanics,1999,32(1):81-100.
[11] LUCAS F M,GONCALVES J P,OLIVEIRA F M,et al.Multiple-site damage in riveted lap-joints:experimental simulation and finite element prediction[J]. International Journal of Fatigue,2000,22(4):319-338.
[12]SHIELDS E B.Fracture prediction of hole patterns with multiple cracks using the finite element method[J].International Journal of Fatigue:Materials Structures,2001,23(1):13-20.
