再论圆管明渠均匀流正常水深的直接计算公式
2012-09-06李风玲
文 辉,李风玲
(惠州学院建筑与土木工程系,广东 惠州 516007)
圆管具有结构形式简单和力学条件好等特点,是给水排水工程和水利工程中应用最广泛的输水形式。但圆管均匀流方程和临界流方程均为超越函数方程,求解这些含三角函数的高次隐函数方程,是十分复杂和困难的,无论是采用查图、查表还是迭代试算或是编程计算都比较繁琐。为此,国内不少学者对正常水深的直接计算[1-7]和临界水深的直接计算[8-11]都作了较深入的研究,得到一些近似的直接计算公式,但存在着公式形式复杂或计算精度不高等诸多缺陷,一定程度上影响了公式的使用与推广,其中王正中的反余弦函数公式[3]最简捷,只是精度稍差,本文将以此为基础,开展进一步研究。
1 圆管明渠均匀流正常水深的基本方程
圆管明渠的正常水深采用均匀流计算公式,以曼宁公式表示的圆管明渠均匀流基本方程[12]为

式中:Q为设计流量,m3/s;i为管道坡降;A为圆管断面过水面积,m2;n为糙率;χ为湿周,m。
1.1 圆管明渠的水力要素
圆管断面如图1所示。圆管明渠的水力要素计算公式为
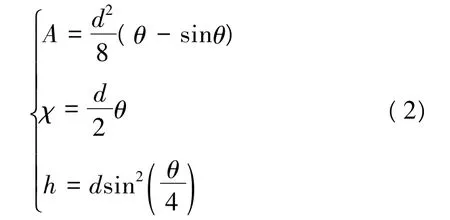
式中:d为圆管直径,m;θ为过水断面充满角,rad;h为正常水深,m。
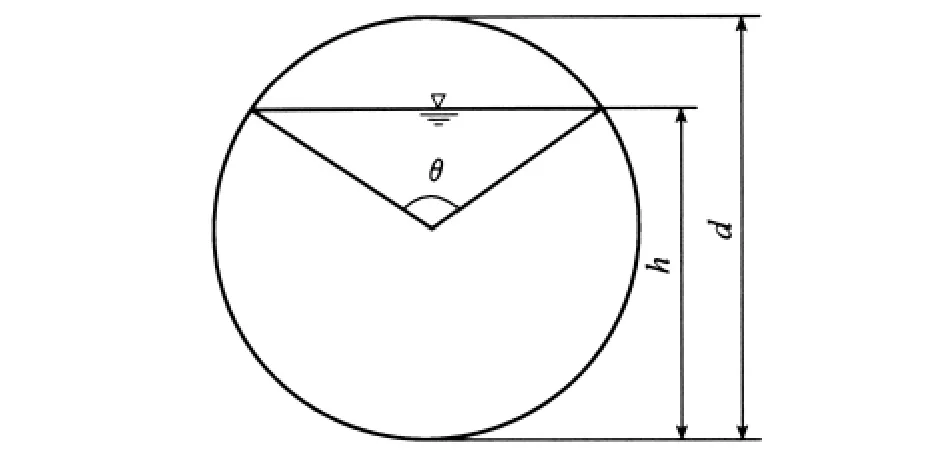
图1 圆管断面
1.2 圆管明渠均匀流正常水深的非线性方程
将式(2)代入式(1),整理便得求解圆管明渠均匀流正常水深的非线性方程:
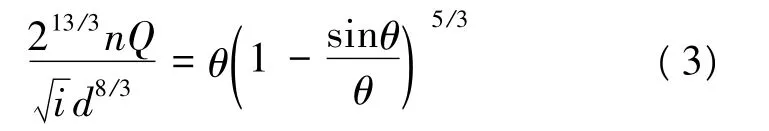
由此可知,圆管明渠均匀流正常水深的计算就是非线性方程式(3)的求根问题。公式左侧为圆管和水流的已知量,为了方便研究,令

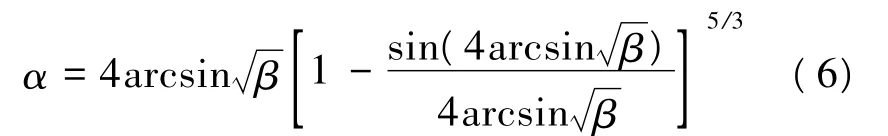
此方程为三角函数方程,无法直接求解。
1.3 圆管明渠均匀流正常水深计算公式的适用范围
理论上正常水深的适用范围应为0≤β≤1,目的是为了防止因水位的细微变化或波浪等的影响而导致明满流交替或封顶的现象发生,保证水面以上空气畅通及水流状态稳定。给水排水工程规范和水利工程规范等要求净空面积不应小于隧洞断面面积的15%,据此得出计算公式的适用上限为
式中:α为无量纲参数;β为无量纲正常水深(正常水深和圆管直径之比)。
将式(4)和式(5)代入式(3)可得:
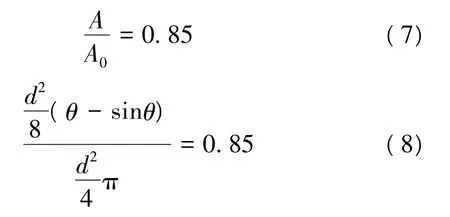
式中:A0为圆管断面面积。
公式(8)为三角超越方程,试算解得 θ=4.3917,所以h上=0.80d。
考虑到大多数工程实际应用情况,过小水深没有太大实际意义,故下限值h下=0.10d,所以正常水深计算公式的工程适用范围为0.1≤β≤0.8。
2 圆管明渠均匀流正常水深的新计算公式
公式(6)为三角函数方程,本文将以反余弦函数构造计算公式形式,通过曲线拟合和优化原理,兼顾公式简捷和结果精度,提出新的计算公式:
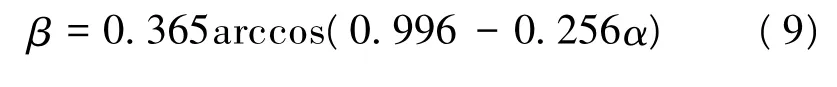
3 误差分析和公式评价
目前主要的几种圆管明渠均匀流正常水深的直接计算公式为
a. 韩会玲公式[1]:
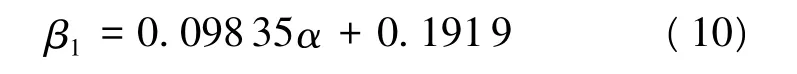
b. 陈水俤公式[2]:

c. 王正中公式[3]:

d. 文辉公式[4]:
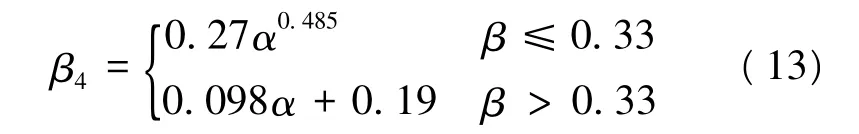
e. 赵延风公式[5]:

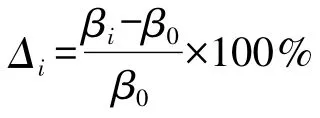
由表1可知:韩会玲公式属于线性函数形式,形式最简单,但误差最大,最大相对误差为104.80%;陈水俤公式属于分段函数形式,形式最复杂,误差很大,最大相对误差为-6.90%;王正中公式属于三角函数形式,形式简单,误差大,最大相对误差为-3.83%;文辉公式也属于分段函数形式,形式较复杂,误差较大,最大相对误差为1.26%;赵延风公式属于指数函数形式,形式较复杂,误差较小,最大相对误差为0.73%;本文公式也属于三角函数形式,形式简单且误差最小,最大相对误差为0.71%。
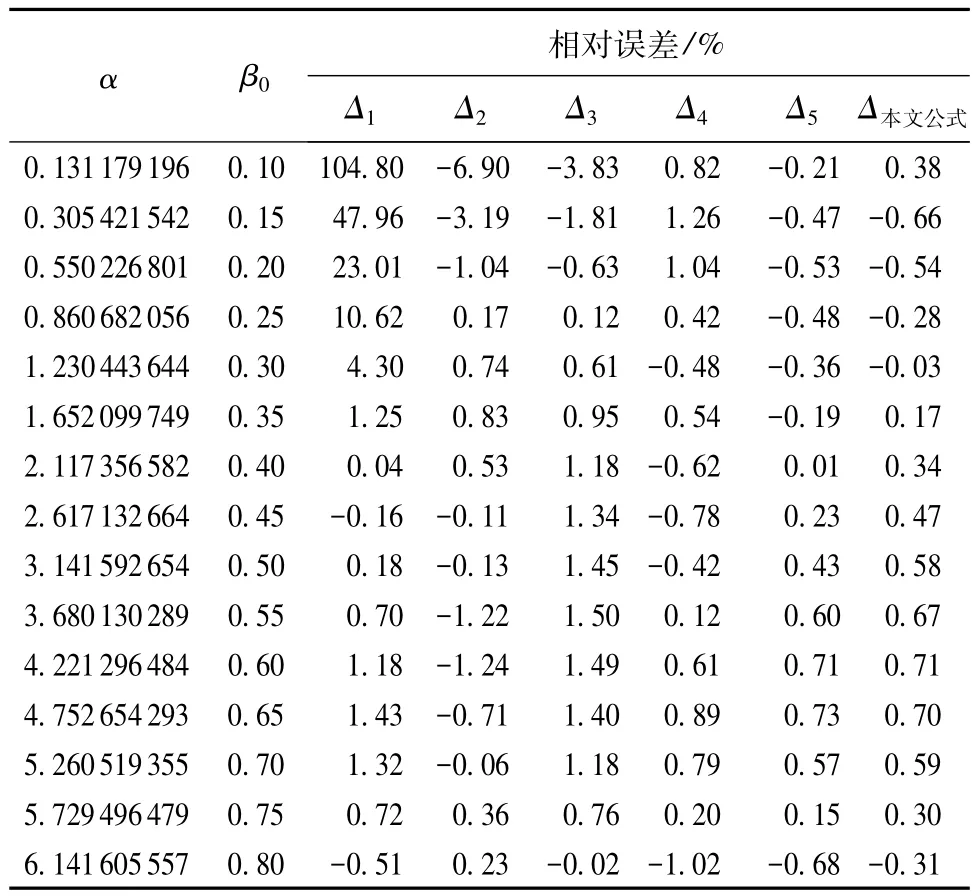
表1 误差分析
4 计算步骤及算例
4.1 计算步骤
a.根据流量Q、管道粗糙系数n、管道直径d和管道坡度i,由式(4)求参数α。b.将α代入式(9)求得无量纲正常水深β。c.将β代入式(5)求得正常水深h。
4.2 算例
某圆形输水隧洞,直径d=6.0 m,洞底坡度i=0.001,粗糙系数n=0.014,流量Q=80m3/s时的均匀流正常水深h可计算如下:
由式(4)可解得 α=6.006 36,由式(9)可解得β=0.782257,再由式(5)计算得h=βd=4.694 m,经试算得到正常水深的精确解 4.696 m,相对误差为-0.051%。
5 结语
本文提出了一个新的圆管明渠均匀流正常水深的直接计算公式,误差分析及实例计算表明,与目前相关文献的研究成果相比,该公式具有表达形式简单且误差小的特点,可极大方便工程设计人员在圆形断面水利工程设计中的直接使用。
:
[1]韩会玲,孟庆芝.非满流圆管均匀流水力计算的近似数值解法[J].给水排水,1994(10):25-26.
[2]陈水俤.排水管道纯公式水力计算[J].给水排水,1995(1):16-17.
[3]王正中,冷畅俭,娄宗科.圆管均匀流水力计算的近似公式[J].给水排水,1997(9):27-29.
[4]文辉,李风玲.圆管明渠均匀流的新近似计算公式[J].人民黄河,2006,28(2):67-69.
[5]赵延风,祝晗英,王正中.一种新的圆形过水断面正常水深近似计算公式[J].河海大学学报:自然科学版,2010,38(1):68-71.
[6]吕宏兴,把多铎,宋松柏.无压流圆形过水断面水力计算的迭代法[J].长江科学院院报,2003,20(5):15-17.
[7]赵延风,芦琴,张宽地.圆形过水断面均匀流水深的近似计算公式[J].西北农林科技大学学报:自然科学版,2008,36(5):225-228.
[8]张宽地,吕宏兴,赵延风.明流条件下圆形隧洞正常水深与临界水深的直接计算[J].农业工程学报,2009,25(3):1-5.
[9]王正中,陈涛,万斌.圆形断面临界水深的新近似计算公式[J].长江科学院院报,2004,21(2):1-2.
[10]文辉,李风玲.圆管明渠临界水深的直接近似计算公式[J].人民黄河,2007,29(4):67-69.
[11]李风玲,文辉,彭波.圆形过水断面临界流的近似水力计算 [J].人民长江,2008,39(11):77-78.
[12]吴持恭.水力学[M].北京:高等教育出版社,1982.
