天然气饱和度对岩石弹性参数影响的数值研究

姜黎明，孙建孟，刘学锋，王海涛

（1.中国石油大学地球科学与技术学院，山东青岛266555；2.中国石油大学理学院，山东青岛266555）

天然气饱和度对岩石弹性参数影响的数值研究

姜黎明1，孙建孟1，刘学锋2，王海涛1

（1.中国石油大学地球科学与技术学院，山东青岛266555；2.中国石油大学理学院，山东青岛266555）

基于三维数字岩心，对岩石的弹性模量、纵横波速度、拉梅常数、泊松比等参数随不同含气饱和度变化规律进行数值研究。研究结果表明岩石的含气饱和度对横波速度影响不大，含气饱和度的增加将引起横波速度的缓慢增加。岩石的拉梅常数、泊松比、纵波速度、弹性模量和纵横波速度比随含气饱和度的增加而减小，当含气饱和度较低时，它们随含气饱和度增加急剧降低。将各弹性参数随含气饱和度的变化率进行比较，发现对天然气饱和度变化最敏感的参数是拉梅常数，其次是泊松比、体积模量和纵横波速度比等。该研究有助于选取对天然气饱和度变化敏感的参数计算储层的含气饱和度，从而提高计算精度。

三维数字岩心；弹性参数；有限元方法；Gassmann－Wood理论；横波速度；拉梅常数

0 引 言

地球物理资料的定性解释需要了解岩石物理性质和岩石微观结构的关系。随着计算机技术的发展，可以根据岩石微观结构信息重建反映岩石真实孔隙空间的三维数字岩心，通过在三维数字岩心上进行岩石物理实验模拟，从而计算岩石的宏观物理性质（如弹性模量、电导率等）。这种方法被称为数字岩石物理或计算岩石物理，可以用于模拟孔隙结构、裂缝和流体对岩石声学性质和电学性质的影响［1－3］。

多孔岩石的弹性性质主要受岩石的孔隙结构、固体相以及流体性质的影响。岩石孔隙中的流体及其变化对岩石的弹性性质产生一定的影响。定量研究岩石弹性力学性质随所含流体变化的特征对于深入了解岩石物理性质，特别是对油气田开发具有重要意义［4］。许多学者通过实验观测的方法研究了孔隙度、泥质含量、流体性质等对岩石声波速度的影响［5－7］，由于饱和气实验对实验设备要求比较高，一般很难实现。本文基于三维数字岩心，对岩石的弹性模量、纵横波速度、拉梅常数、泊松比等参数随不同含气饱和度变化规律进行了数值实验研究。

1 数字岩心的建立

建立数字岩心的方法主要有3种：切片组合法、X射线CT法和基于岩石二维图像分析的重建法。其中，切片组合法需要花费很长时间制备大量的岩心切片，因而极少被采用。X射线CT法是建立数字岩心最直接、最准确的方法，但由于实验成本过高，限制了该项技术的广泛应用。X射线CT法重建三维图像的主要步骤：首先通过X射线CT扫描得到与样品X射线吸收系数有关的投影数据，然后通过重建算法（如卷积滤波法和迭代法），将其转换为一系列的岩心横截面二维图像，将岩心的二维横截面图像组合便得到岩心的三维灰度图像，最后通过对灰度图像进行图像分割，得到研究所需的三维二值图像即三维数组。基于岩石二维图像分析的重建算法只需要极少量岩石切片的扫描图像，其获取方便、经济，因此该方法具有重要的应用价值［8］。

基于岩石二维图像分析的重建算法分为2类：随机法和过程法。随机法是在岩石二维图像统计函数的约束下调整随机场中孔隙和骨架的位置，使随机场和二维图像具有相同的统计特性，从而构建三维数字岩心。高斯场法［9］和模拟退火算法［10］是应用较为普遍的随机法。随机法重建数字岩心孔隙连通性较差，但适用性强。过程法重建数字岩心是结合岩石颗粒的粒径分布，通过对沉积类岩石的形成过程（包括沉积、压实和成岩作用）的模拟建立数字岩心［11－12］。过程法重建的数字岩心更接近真实岩心。

本文选用4块通过X射线CT构建的数字岩心，孔隙度分别为8%、13%、19%、21%，渗透率范围是80～3 000mD＊＊非法定计量单位，1mD＝9.87×10－4μm2，下同（见图1）。图1中蓝色代表岩石骨架，红色代表孔隙。由于岩石物理性质受岩石尺寸的影响，因此在研究中选了代表元体积（REV），通过多次测试验证表明当数字岩心大小为200×200×200体素时，岩心的物理性质（比如孔隙度、弹性模量）不再受岩心尺寸的影响。所以在研究中，选代表元体积为200×200×200体素。

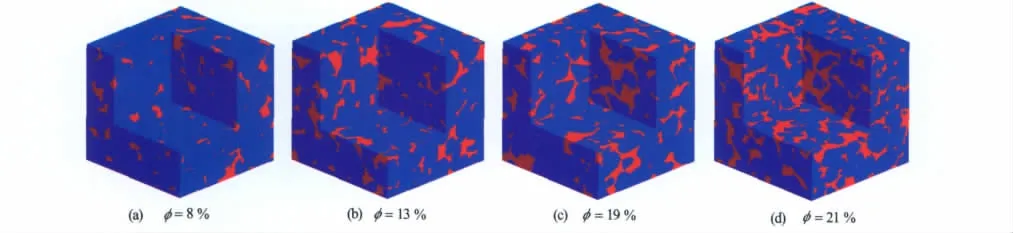
图1 X射线CT获取的枫丹白露砂岩三维数字岩心

2 理论和数值模拟方法

2.1 流体替换：Gassmann理论

Gassmann理论是研究流体饱和对岩石声波速度影响的最常用理论。该理论把饱和流体孔隙岩石的弹性模量与干岩石骨架的弹性模量、固体颗粒弹性模量和孔隙流体的弹性模量联系起来。流体饱和岩石的体积模量K为

如果孔隙空间被n种流体的混合物所填充，则混合流体的体积模量可以由Wood方程［5］给出

式中，xi和Ki分别为第i种流体相的体积含量和体积模量。对于气和水2种复合流体，式（2）可写为

式中，Sw为含水饱和度；Kw和Kg分别为水和气的体积模量。把式（3）的流体模量Kf代入式（1）便可得到计算两相流体饱和岩石体积模量的Gassmann－Wood（GW）方程

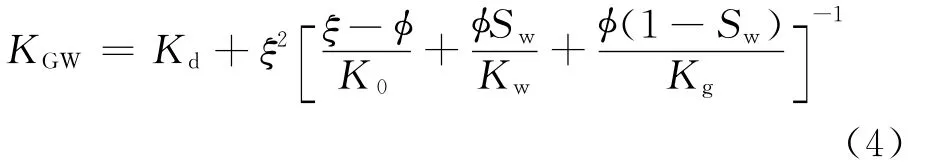
由此可计算单相和多相流体饱和岩石的有效弹性模量，进而得到岩石的纵波速度vp、横波速度vs、纵波阻抗Ip、拉梅常数λ及泊松比σ等。饱和流体岩石密度与孔隙度的关系可以表示为

式中，ρ0为固体颗粒的密度；ρf为孔隙流体的密度。岩石弹性参数可由以下弹性方程得到

2.2 有限元法

有限元法非常适合基于多孔岩石的微观结构预测岩石的有效弹性性质［14］，并且可以用来处理具有任何体素的微观结构。给定固体组分和流体相的体积和剪切模量，就可以基于多孔岩石的三维微观结构用有限元的方法研究岩石的宏观物理性质，比如岩石的有效弹性模量。在三维数字岩心的基础上，利用有限元法计算岩石弹性模量的理论基础是变分原理。对于一个给定的数字岩心，施加一个宏观应变，利用快速共轭梯度的方法通过把体系的弹性自由能最小化来求取由这个外加应变引起的平均应力，从而求取岩石的有效弹性模量。首先把三维数字岩心离散化，离散后的每一个三维的体素都看成是1个三线性的有限元。实际计算的精确性取决于离散的误差，分割的三维体素越多，误差越小。然而，体素的多少又取决于计算机的内存和计算速度（每个体素占内存230B）。考虑到计算机存储和运算能力的限制，本文研究中取200×200×200体素。

3 数值模拟结果和讨论

本文基于三维数字岩心利用有限元的方法模拟了含气饱和度对岩石弹性性质的影响，在数值模拟中，岩石骨架和孔隙流体的弹性参数取值见表1。

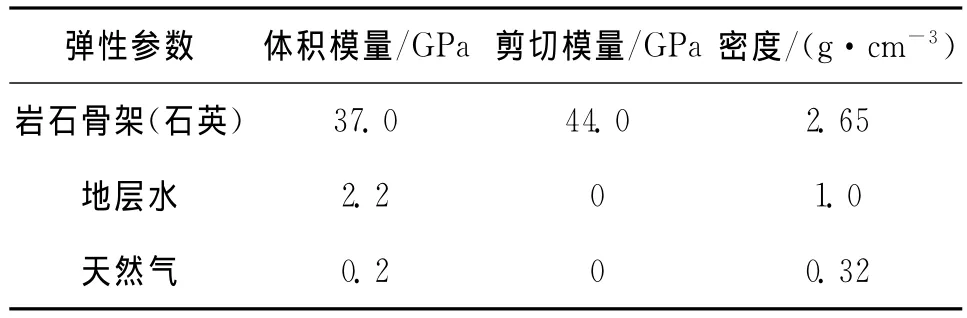
表1 岩石的弹性参数＊

对于两相流体饱和岩石，利用格子玻尔兹曼方法［15］确定三维数字岩心孔隙空间的流体分布。图2是孔隙度为19%的枫丹白露砂岩（亲水岩石）在不同含气饱和度下流体分布图，其中蓝色代表岩石骨架，红色代表天然气，绿色代表水。

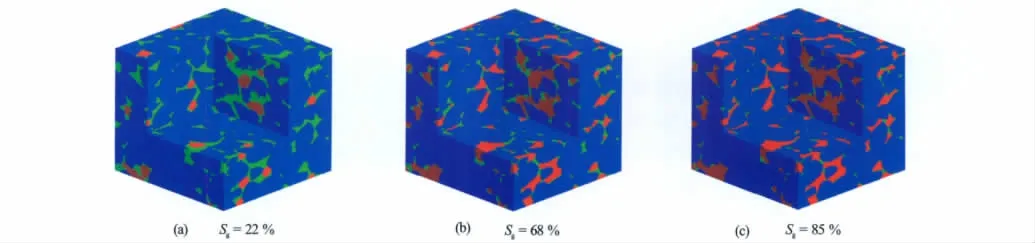
图2 不同含气饱和度下的流体分布（亲水岩石）

在不同含气饱和度条件下，孔隙空间的流体分布不同，岩石的弹性模量会受到流体分布和流体性质的影响。首先利用格子玻尔兹曼方法确定了不同含气饱和度下孔隙空间的流体分布，然后基于三维数字岩心利用有限元方法计算了岩石的体积模量和剪切模量，研究了含气饱和度和弹性模量的关系并和GW理论进行了比较，具体计算结果见图3。从图3可见，在整个含气饱和度范围内，有限元的数值模拟结果与GW理论计算结果基本吻合，这说明基于三维数字岩心利用有限元方法计算两相流体饱和岩石的弹性模量是可行的。从图3还可以看出随含气饱和度的增加，岩石的体积模量减小，这是因为气含量的增加导致了岩石的压缩性增大，岩石的剪切模量不受流体变化的影响。

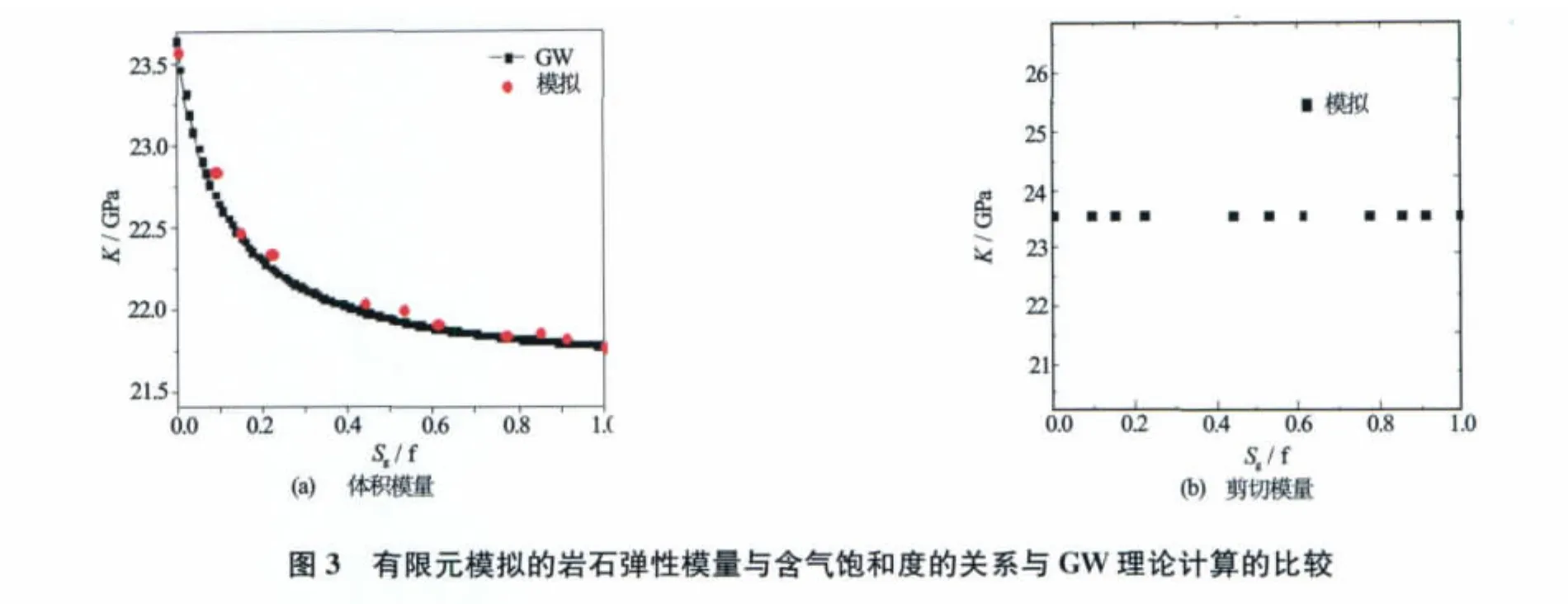
图4分别给出了岩石拉梅常数、泊松比、纵横波速度、弹性模量及纵横波速度比随含气饱和度的变化关系曲线。岩石的含气饱和度对横波速度影响不大，它的增加将引起横波速度缓慢增加，这主要是因为含气饱和度增加，导致了岩石密度降低。岩石的拉梅常数、泊松比、纵波速度、弹性模量和纵横波速度比随含气饱和度的增加而减小，当含气饱和度较低时，以上弹性参数随含气饱和度增加急剧降低。也就是说这些弹性参数在含水饱和度较高时，对于气体含量非常敏感，当含有较多气体时，它们对气体含量不很敏感。

对于天然气储层，气体的储集会引起整个储集层的弹性模量、拉梅常数、泊松比、纵波速度、弹性模量及纵横波速度比明显降低，而横波速度略有升高。为了研究各弹性参数对含气饱和度变化的敏感性，定义弹性参数随含气饱和度相对变化率

式中，ypg和yg分别表示部分饱和气和完全饱和气岩石的弹性参数。

图5将各弹性参数随含气饱和度的变化率进行了比较。对含气饱和度变化最敏感的参数是拉梅常数，其次是泊松比、体积模量和纵横波速度比，特别是当含气饱和度较小的时候，含气饱和度的变化能引起这些弹性参数的明显变化。在结合测井资料计算岩石含气饱和度时，可以选择对含气饱和度变化反应敏感的参数计算。首先要选择拉梅常数，其次是泊松比、体积模量和纵横波速度比，这样可以减小计算误差，提高计算精度。

图5 岩石弹性参数的相对变化率与含气饱和度的关系

4 结 论

（1）把数值模拟结果与理论计算结果进行了比较，发现在整个含气饱和度范围内，有限元的数值模拟结果与GW理论计算结果基本吻合，证明了数值研究方法的可行性。

（2）岩石的含气饱和度对横波速度影响不大，它的增加将引起横波速度缓慢增加；岩石的拉梅常数、泊松比、纵波速度、弹性模量和纵横波速度比随含气饱和度的增加而减小，当含气饱和度较低时，它们随含气饱和度增加急剧降低，说明这些弹性参数在含水饱和度较高时，对于气体含量非常敏感，当含有较多气体时，它们对气体含量不很敏感。

（3）将各弹性参数随不同含气饱和度的变化率进行了比较，发现对含气饱和度变化最敏感的参数是拉梅常数，其次是泊松比、体积模量和纵横波速度比。该研究有助于选取对含气饱和度变化敏感的参数计算储层的含气饱和度，从而提高计算精度。

［1］ Meille S，Garboczi E J.Linear Elastic Properties of 2D and 3DModels of Porous Materials Made from Elongated Objects［J］.Modelling Simul.Mater.Sci.Eng，2001，9（1）：371－390.

［2］ Knackstedt M A，Arns C H，Sheppard A P，et al.Archie’s Exponents in Complex Lithologies Derived from 3DDigital Core Analysis［C］∥The SPWLA 48th Annual Logging Symposium，paper UU，Austin：2007.

［3］ Jiang Liming，Sun Jianmeng，Liu Xuefeng，et al.Study of Different Factors Affecting the Electrical Properties of Natural Gas Reservoir Rocks Based on Digital Cores［J］.Journal of Geophysics and Engineering，2011，8（2）：366－371.

［4］ 杜韫华，钱凯，张守鹏，等.中国天然气储层的岩石、古地理类型与勘探方向［J］.石油与天然气地质，1999，20（2）：140－143.

［5］ King M S，Marsden J R，Dennis J W.Biot Dispersion for P－and S－wave Velocity in Partially and Fully Saturated Sandstone［J］.Geophysical Prospecting，2000，48（6）：1075－1089.

［6］ Clark V A.The Effect of Oil under In－situ Conditions on the Seismic Properties of Rocks［J］.Geophysics，1992，57（7）：894－901.

［7］ 李生杰.岩性、孔隙及其流体变化对岩石弹性性质的影响［J］.石油与天然气地质，2005，26（6）：760－764.

［8］ 姚军，赵秀才，衣艳静，等.数字岩心技术现状及展望［J］.油气地质与采收率，2005，12（6）：52－54.

［9］ Adler P M，J acquin C G，Quiblier J A.Flow in Simulated Porous Media［J］.International Journal of Multiphase Flow，1990，16（4）：691－712.

［10］Hazlett R D.Statistical Characterization and Stochastic Modeling of Pore Networks in Relation to Fluid Flow［J］.Mathematical Geology，1997，29（6）：801－822.

［11］Oren P E，Bakke S.Process Based Reconstruction of Sandstones and Prediction of Transport Properties［J］.Transport in Porous Media，2002，46：311－343.

［12］Oren P E，Bakke S.Reconstruction of Berea Sandstone and Pore－scale Modelling of Wettability Effects［J］.Journal of Petroleum Science and Engineering，2003，39：177－199.

［13］Krief M，Garat J，Stellingwerff J，et al.A Petrophysical Interpretation Using the Velocities of P and S Waves（Full－wave Sonic）［C］∥The 12th SPWLA Logging Symposium，Paper HH，Paris：1989.

［14］Garboczi E J，Day A R.Algorithm for Computing the Effective Linear Elastic Properties of Heterogeneous Materials：Three－dimensional Results for Composites with Equal Phase Poisson Ratios［J］.Journal of the Mechanics and Physics of Solids，1995，43（9）：1349－1362.

［15］Pan C，Hilpert M，Miller C T.Lattice－Boltzmann Simulation of Two－phase Flow in Porous Media［J］.Water Resources Research，2004，40：W01501.

Numerical Study of the Effect of Natural Gas Saturation on the Reservoir Rocks’Elastic Parameters

JIANG Liming1，SUN Jianmeng1，LIU Xuefeng2，WANG Haitao1
（1.School of Geo－sciences，China University of Petroleum，Qingdao，Shandong 266555，China；2.College of Science，China University of Petroleum，Qingdao，Shandong 266555，China）

The variation law of the effect of natural gas saturation on the reservoir rocks’elastic parameters，such as elastic moduli，P－wave and S－wave velocities，Laméconstant，Poisson’s ratio，is studied based on 3Ddigital cores.The results show that gas saturation of reservoir rocks has little influence on S－wave velocity and the S－wave velocity increases slowly with the increase of gas saturation.The elastic parameters，such as Laméconstant，Poisson’s ratio，P－wave velocity，the ratio of P－wave velocity to S－wave velocity，decrease as the gas saturation increases.Moreover，they are changed sharply when the sandstone contains very small amount of gas.After comparing the change ratios of the elastic parameters with the variation of gas saturation，it is found the Laméconstant is most sensitive to the variation of gas saturation，followed by Poisson’s ratio，bulk modulus and the ratio of P－wave velocity to S－wave velocity.Through this study，the parameter which is sensitive to change of gas saturation can be used to calculate gas saturation of reservoir rocks in order to improve the calculation accuracy.

3Ddigital core，elastic parameter，finite element method，Gassmann－Wood theory，S－wave velocity，Laméconstant

TE19

A

2011－05－13 本文编辑 王小宁）

1004－1338（2012）03－0239－05

国家863高技术研究发展计划项目（2006AA060105）

姜黎明，男，1983年生，博士研究生，从事岩石物理数值模拟及测井解释研究。