利用径向基函数预测岩石渗透率及流体分子组分

邹友龙，胡法龙，李长喜，李潮流

（1.中国石油勘探开发研究院测井与遥感技术研究所，北京100083；2.中国地质大学地球物理与信息技术学院，北京100083）

利用径向基函数预测岩石渗透率及流体分子组分

邹友龙1，2，胡法龙1，李长喜1，李潮流1

（1.中国石油勘探开发研究院测井与遥感技术研究所，北京100083；2.中国地质大学地球物理与信息技术学院，北京100083）

测井反问题研究中，经常遇到正演模型未知、经验公式的相关系数较小的情形，且现有的反问题处理方法难以获得理想的效果。径向基函数插值方法是目前最有效的反问题处理方法之一，该技术能够生成平滑连续的多个变量的多元函数，逼近未知的正演模型。介绍径向基函数插值方法原理，针对核磁共振实验的T2分布，采用径向基函数插值方法预测了岩石渗透率及流体分子组分，实现了多维到一维映射及多维到多维映射的2种情况，并且预测结果具有较高精度，测量值的对比验证了该方法解决测井反问题的有效性。

测井反问题；正演模型；径向基函数插值；渗透率；分子组分

0 引 言

在测井反问题中，精确的正演模型往往未知。现有计算渗透率的经验模型为Coates模型［1］和SDR模型［2］，Freed［3］和Heaton［4］等曾尝试利用弛豫时间和扩散系数分布建立与分子组分的物理模型。但是经验公式经常会遇到相关系数低、误差较大的情况，主要原因是采用的输入信息太少，受地区和地质条件等多重因素影响较大。经验公式常常是多维输入到一维输出的映射，对于多维输入到多维输出的映射，经验公式无法实现。2006年Freedman［5］提出了利用径向基函数（RBF）插值的方法处理岩心数据分析中遇到的一些反问题，并且取得一定应用效果。径向基函数像软膜一样通过各个已知的样本数据点，生成连续光滑的多变量多元函数可以逼近正演模型。本文采用径向基函数插值方法，利用T2分布分别预测岩石渗透率与流体分子组分，实现了多维到一维映射及多维到多维映射的2种情况，并且预测结果具有较高精度，验证了利用径向基函数解决测井反问题的有效性，为测井解释中关键参数获取提供了一个新思路。

1 径向基函数插值原理

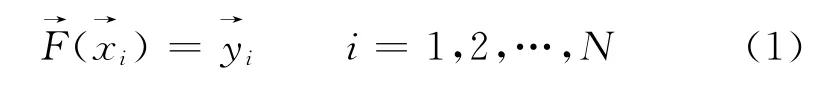
逼近函数形式为

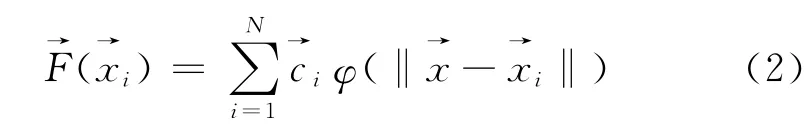
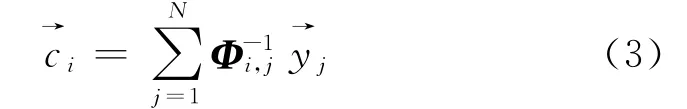
若矩阵的条件数较大或者实验数据具有误差时，此时可取正则化解

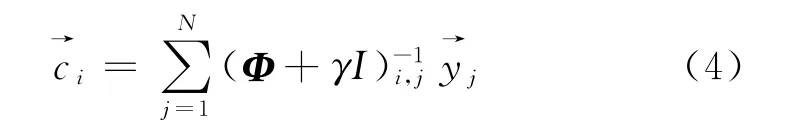
采用高斯径向基函数，即

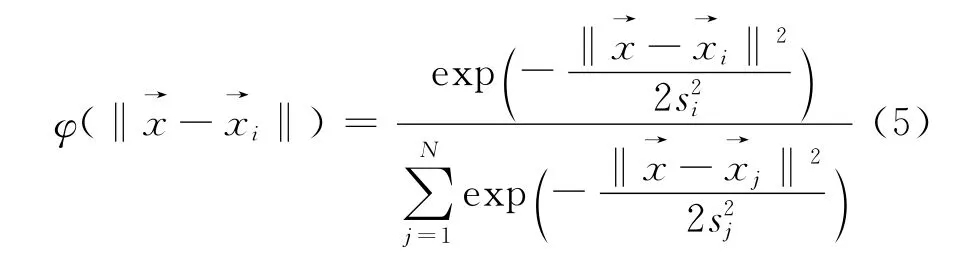
式中，si为高斯函数的宽度。s的选取直接影响到预测结果的好坏，它的取值与最邻近距离（NND）成正比，s＝α·NND，α为比例常数。联合式（2）和式（5）有

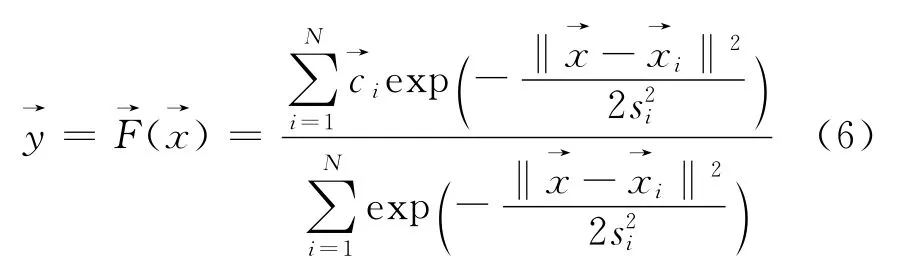
因此，系数解的矩阵形式为

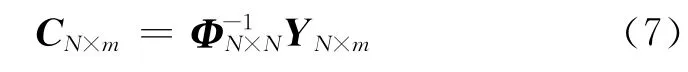
式中，N为样品的个数；m为样品预测的属性个数；

考虑到各向异性的问题，φi，j写为

将式（6）改写为

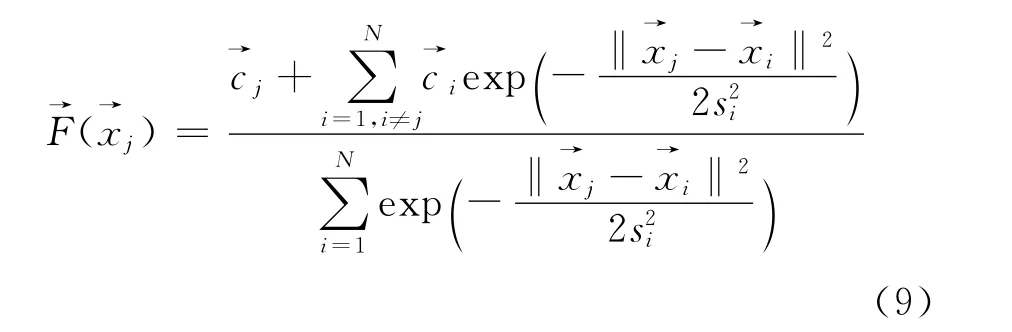
如果忽略径向基函数之间的重叠，即当高斯函数的宽度足够小时，式（9）可简写为

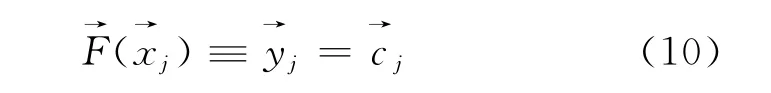
因此，由式（9）和式（10）有

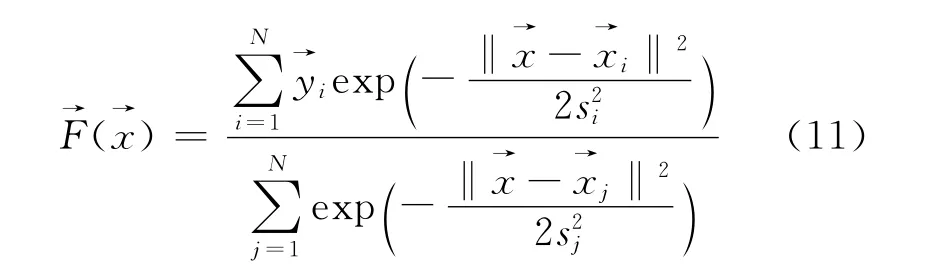
其次，美国政府具有制裁规则制定者和执行者的双重身份。制裁政策主要由以海外资产控制办公室为核心的财政部及相关部门起草制定，对于政策的解读和澄清也主要由财政部负责，海外资产控制办公室的大量解释性指导意见和常见问题回答则是制裁政策的重要执行依据，以财政部为核心的政府相关部门会通力配合实施制裁。因此，美国政府对于制裁谁和如何制裁具有完全的决策权威。

2 应用实例

核磁共振测井获得的数据T2分布是一个二维数据，而现有渗透率模型均采用基于T2分布的某些特定参数，如T2几何均值、自由流体指数和束缚流体指数等，无法将T2分布中所有数据信息应用到渗透率计算中，其渗透率求取效果并不理想。2001年Freedman等人发现弛豫时间和扩散系数可以提供分子组分的信息［7］，并试图推导出相互之间的物理模型［3－4］，然而原油是含烃分子的复杂混合物，推导出准确的物理模型非常困难［5］。径向基函数在解决多维数据反问题的研究中优势明显，以下利用径向基函数技术分别实现T2分布求取渗透率与分子组分，准确获得了测井解释中的关键参数。

本文采用的是leave－one－out方法［5］，即从所有的样本中取出1颗待预测的岩心，然后利用剩下的所有岩心数据求解得到系数矩阵C，得到构造函数），最后计算得到取出岩心的预测值，这样依次循环对每颗岩心进行预测。通过对预测结果与测量值的比较，发现该方法运用效果较好。

2.1 T2分布预测渗透率

试验样品来自渤海湾盆地东营组岩心资料，主要包括基础孔隙度、渗透率和核磁共振岩心分析数据。图1所示为东营组12颗岩心经过核磁共振实验得到的T2分布及其对应的渗透率，12颗岩心的核磁共振实验和渗透率数据均在相同条件下测定。

图1 东营组12颗岩心的T2分布及其渗透率

由径向基函数插值原理可知，预测渗透率的径向基映射函数可写为

为了对比RBF插值方法的效果，利用SDR模型，得到渗透率计算公式为

式中，φ为孔隙度；T2，gm为T2几何均值。图2为渗透率K与×φ4的交会图，从图2中可以看到，两者之间的拟合关系较差。

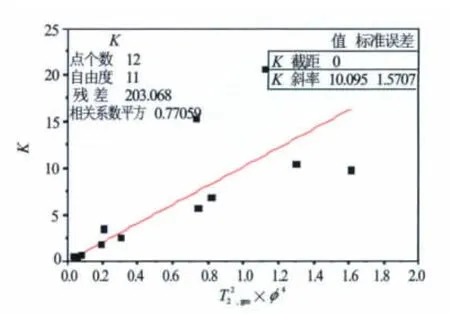
图2 渗透率K与×φ4交会图

式中，log vm为测量值取自然对数；log vp为预测值取自然对数。

图3为经验公式计算的渗透率与测量渗透率的对比图，对应的误差χ2为1.743 8。由于系数α的选取直接影响预测效果的好坏，通过考察α对预测结果的影响，选取α的最佳值。取α以0.05为步长从0.1～2.0变化。图4为预测值与测量值的误差χ2随α的变化关系。从图4中可以看出α的最优值在0.4～0.7左右。图5为α＝0.65时预测结果与测量值的对比，预测渗透率与测量渗透率的误差在1倍范围之内，相应的预测值与测量值误差χ2为 0.513 8小于SDR模型预测结果的误差，预测结果的精度较高。

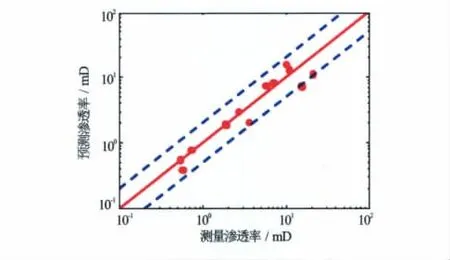
图3 经验公式计算的渗透率与测量结果对比

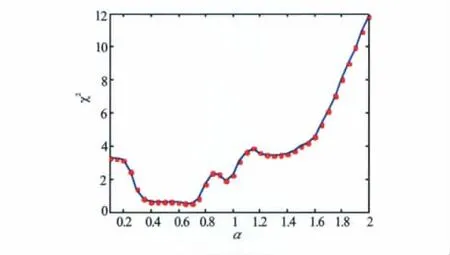
图4 预测渗透率与测量结果的误差随α的变化

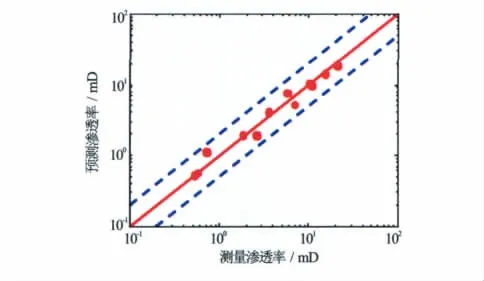
图5 α＝0.65时预测渗透率与测量结果的对比

2.2 T2分布预测流体分子组分

原油的分子组分是评价储层质量，产能和划分的一个关键参数［8］。原油是含烃分子的复杂混合物，而核磁共振测井能为井下含氢流体的定性及定量分析提供重要资料，因此核磁共振测井资料可用来分析原油的组分。利用径向基函数插值的方法运用T2分布预测流体分子组成，其中T2分布与分子组分数据均采用Freedman文献中的T2分布与分子组分数据。预测分子组分的径向基映射函数形式与式（12）一致，输出参数为分子组分向量，输入参数为经过最大值标准化后的T2分布。

该部分的预测值与测量值的误差χ2定义为

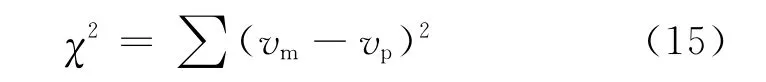
式中，vm为测量值；vp为预测值。

同样考察系数α对预测结果的影响，取α以0.1为步长从0.1～2.5变化。图6为预测值与测量值的误差χ2随α的变化。从图6中可以看出，系数α的最优值在1.4左右，相应的预测值与测量值的误差χ2为1 129.3。图7为α＝1.4时预测的分子组分与测量分子组分的对比，预测值与测量值基本重合，预测效果比较满意。

图6 预测分子组分与测量结果的误差随α的变化

3 结论与建议

（1）径向基函数法为渗透率和分子组分的预测提供了一种新思路，并可推广到其他测井反问题中。

（2）径向基函数法可解决测井中的反问题，且具有以下优点：① 当正演模型未知时，该方法是解决测井反问题的一个很好的工具；② 其不受维数的限制，输入与输出参数都可为多维；③ 相对于经验公式，可考虑的信息量更多，使得逼近函数更加趋近于正演模型。

（3）该方法适用于多维数据输入与多维数据输出的情况，且计算量小运算速度快，这是经验公式和其他方法无法比拟的。

（4）该方法预测的效果受α的影响，α的一般取值范围在0.5～1.5左右，α取值不宜过大，否则预测值接近于实验数据的平均值。

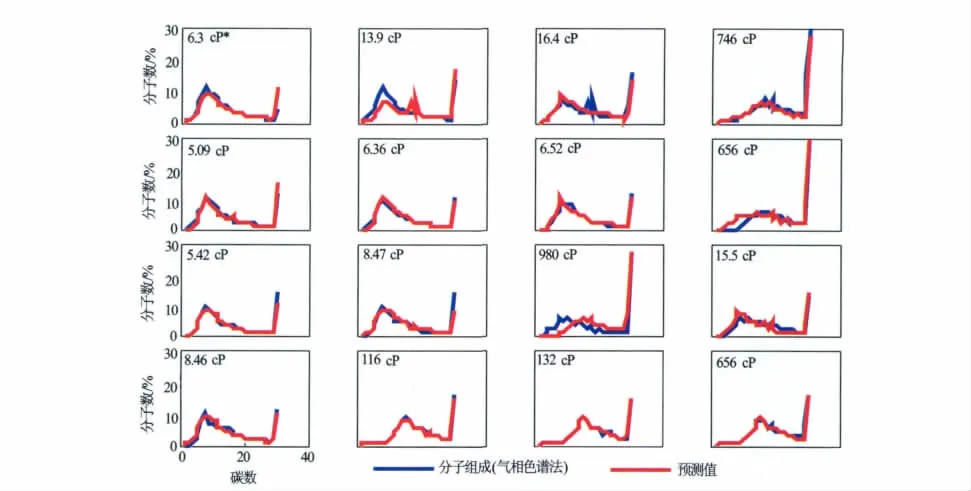
图7 预测分子组分与测量结果对比

（5）虽然该方法具有许多优点，但也存在一些需要解决的问题，如实验数据的误差对预测结果的影响，以及如何自动选取合适的高斯函数宽度。

［1］ Coates G R，Marschall D，Mardon D，et al.A New Characterization of Bulk－volume Irreducible Using Magnetic Resonance［C］∥SPWLA 38th Annual Logging Symposium Transactions：Society of Petrophysicists and Well Log Analysts，Paper QQ，1997.

［2］ Kenyon W E，Day P I，Straley C，et al.A Three－part Study of NMR Longitudinal Relaxation Properties of Water－saturated Sandstones［J］.SPE Formation Evaluation，1988，3：622－636.

［3］ Freed D.Molecular Composition from Diffusion or Relaxation Measurements：US 2004／0253743A1［P］.2004－12－16.

［4］ Heaton N，Freedman R.Method for Determining Molecular Properties of Hydrocarbon Mixtures from NMR Data：U.S.Patent 6 859 032［P］.2005.

［5］ Freedman R.New Approach for Solving Inverse Problems Encountered in Well－logging and Geophysical Applications［J］.Petrophysics，2006，47：93－111.

［6］ Lukaszyk S.A New Concept of Probability Metric and Its Applications in Approximation of Scattered Data Sets［J］.Computational Mechanics，2004，33：299－3004.

［7］ Freedman R，Lo S，Flaum M，Hirasaki G J，et al.A New NMR Method of Fluid Characterization in Reservoir Rocks：Experimental Confirmation and Simulation Results［J］.SPE Journal，2001，4：52－464.

［8］ Anand V，Freedman R.New Methods for Predicting Properties of Live Oils from NMR［C］∥Paper DD in 50th SPWLA Annual Logging Symposium Transactions：Society of Petrophysicists and Well Log Analysts，June 21－24，Paper AAAA，2009.

Prediction of Rock Permeability and Fluid Molecular Composition Using Radial Basis Function

ZOU Youlong1，2，HU Falong1，LI Changxi1，LI Chaoliu1
（1.Research Institute of Petroleum Exploration ＆Development，Beijing 100083，China；2.School of Geophysics ＆Information Technology，China University of Geosciences，Beijing 100083，China）

In logging inverse problem research，the forward models are often unknown and correlation coefficients of empirical equations are small，and the existing inverse problem approaches are difficult to obtain the desired results.Radial basis function（RBF）interpolation is one of the most effective approaches to deal with inverse problems，which can generate smooth and continuous multivariate functions of many variables to approximate the forward mode.Introduced is the theory of RBF interpolation.According to T2distributions of the NMR experiments，predicted are rock permeability and fluid molecular compositions using RBF interpolation method.Achieved are mapping from multi－dimensional to one－dimensional and from multi－dimensional to multi－dimensional，and prediction accuracy is high.Verified is the validity of RBF interpolation method to solve the logging inverse problems by comparing the predicted results with measurements.

logging inverse problem，forward model，radial basis function（RBF）interpolation，permeability，molecular composition

P631.84

A

2011－12－12 本文编辑 余迎）

1004－1338（2012）03－0225－05

邹友龙，男，1988年生，硕士研究生，从事测井资料反演与岩石物理实验分析研究。