矩形通道内气泡脱离点数值模拟和实验研究
2012-09-03朱明章高璞珍刘智华
朱明章,高璞珍,刘智华
(1.哈尔滨工程大学核科学与技术学院,黑龙江哈尔滨150001;2.西安交通大学核科学与技术学院,陕西西安710049)
过冷沸腾又称为欠热沸腾,是指流体温度尚未达到饱和温度而局部加热壁面温度超过流体饱和温度一定值时造成的沸腾现象[1].过冷沸腾区有2个重要的点,一个是过冷沸腾起始点(ONB);另一个是气泡脱离点,也称为充分发展沸腾起始点(FDB)、净蒸汽产生点(NVG)[2].
气泡脱离点(FDB)是单相流与两相流的分水岭,在这一点前的流动可以按照单相流处理;而在这一点后开始出现气泡,含气率逐渐增加,流动和传热特性相应的会发生变化,需按照两相流来处理.因此,过冷沸腾气泡脱离点的确定对换热设备的传热计算和流体阻力计算等都是非常重要的,它直接关系到下游的流动传热特性,是一个关键环节.
对于过冷沸腾气泡脱离点,现在已经发展出了数十个经验模型关系式,并进行了大量的实验研究工作[3-6].其中 Saha-Zuber模型和 Bowring 模型[2]被认为是预测精度最高的模型,其他众多的模型大多是在这两者的基础上进行了改进得来的.但是用数值模拟的方法来预测气泡脱离点的研究目前还没有成果发表.关于过冷沸腾的数值模拟,Li[7]、Tu[8]、樊普[9]等利用CFD软件,通过UDF建立气泡平均直径模型、气泡脱离直径模型、气泡成核模型、气泡脱离频率模型、欠热沸腾起始点模型和壁面热流密度分配模型等,实现了过冷沸腾的数值模拟[10-11].但这些模拟都针对沸腾发生后特性的研究,缺乏关于过冷沸腾气泡脱离点位置的模拟.本研究建立了数值模拟预测气泡脱离点的物理模型,实现了用数值模拟方法对气泡脱离点的预测,并通过与经典模型公式和实验结果的比较得到验证.
1 数值模拟模型
1.1 问题简化
由于实际问题的复杂性,为了便于模拟,作了以下合理的简化和假设.
1)采用二维模型.
本研究中,圆管通道直径10 mm,长1 m,长径比为100,长度远大于直径,考虑到圆管的轴对称性,采用柱坐标系,建立了二维通道模型.
矩形流道为40 mm×2 mm截面的窄矩形通道,长1 m.宽边远大于窄边,宽度的影响较小,本文忽略宽度的影响,建立了直角坐标系下间距为窄边尺寸2 mm的二维通道模型.
2)网格划分.
对简化的二维通道模型,采用平铺的结构化网格.网格为正方形,边长为0.1 mm.
3)忽略散热损失.
4)认为加热壁面是恒定热流密度,不考虑壁面蓄热的影响.
1.2 UDF定义沸腾相变
过冷沸腾气泡脱离点处流体发生由水到气的沸腾相变,沸腾相变的模拟是实现本文模拟的关键,而Fluent本身不具有相变的模拟功能,所以建立模型,通过Fluent的UDF功能进行定义.本模拟中,通过UDF,定义水和水蒸气的体积转换、能量转换,认为当某个控制体内的平均温度大于饱和温度时,该网格内就会有相应质量的水转化为水蒸气,同时控制体内能量以汽化潜热的形式相互转化.
对于液相来说,控制体质量转换关系为
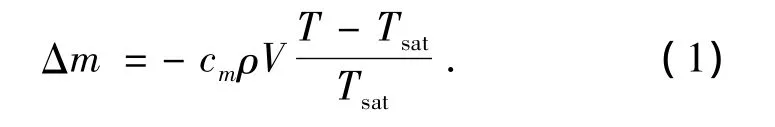
式中:Δm表示从液相转化为汽相的质量;ρ、V、T分别为控制体密度、体积和温度;Tsat为对应控制体压力下饱和温度;cm表示蒸发系数和凝结系数.在本模拟中,只研究过冷沸腾气泡脱离点位置,不考虑沸腾发生后的传热系数、空泡份额等参数,因此cm对本问题没有影响,默认采用0.1.
控制体能量转换关系为)

式中:hgf表示汽化潜热.
1.3 其他设置
1)水和水蒸气物性采用二阶差值函数输入.
2)选择混合模型(mixturemodel),欠松弛因子按教材[12]中多相流模型的推荐值设置,然后将其中的液态水、气态水蒸气的质量源项和能量源项分别选择为用户定义.
3)湍流模型选择RNG k-ε模型和标准壁面函数,湍流模型系数选择软件默认值.
4)重力加速度值g=9.8 m/s2.
5)进口边界条件设置为速度进口,出口边界条件设置为压力出口.
6)壁面设置为无滑移壁面,加热壁面设置恒定热流密度值,其他壁面为绝热.
1.4 后处理
对计算的结果进行后处理,绘制体积含气率图,从图中找出体积含气率开始大于零的位置,认为此点为气泡脱离点.
根据上述模型和方法,本文用Fluent软件模拟了圆管通道和窄矩形通道中的过冷沸腾气泡脱离点.
2 模拟结果与经典模型对比
经典的Saha-Zuber模型和Bowring模型[2]是根据在圆管通道内的实验结果提出的经验公式,为了验证本文模拟结果的准确性,首先对比了圆管内模拟结果与经典模型计算值,然后分析了矩形通道内模拟结果与经典模型计算值,检验数值模拟方法和经典模型在矩形通道内的适用性.
2.1 圆管通道验证
图1是热流密度为800 kW/m2时,直径为10 mm的圆管通道中气泡脱离点(FDB)位置随流速的变化曲线.通过对比发现数值模拟结果与Saha-Zuber模型达到了很好的吻合,这说明了数值模拟的可行性与准确性,证明了本文为数值模拟所建立的模型是合理的,也为进一步采用数值模拟方法研究矩形通道内气泡脱离点打下了基础.但是数值模拟结果与Bowring模型存在较大的偏差,这主要是因为各个模型都有各自的适用范围,Bowring模型在
本计算例的参数下不如Saha-Zuber模型准确.
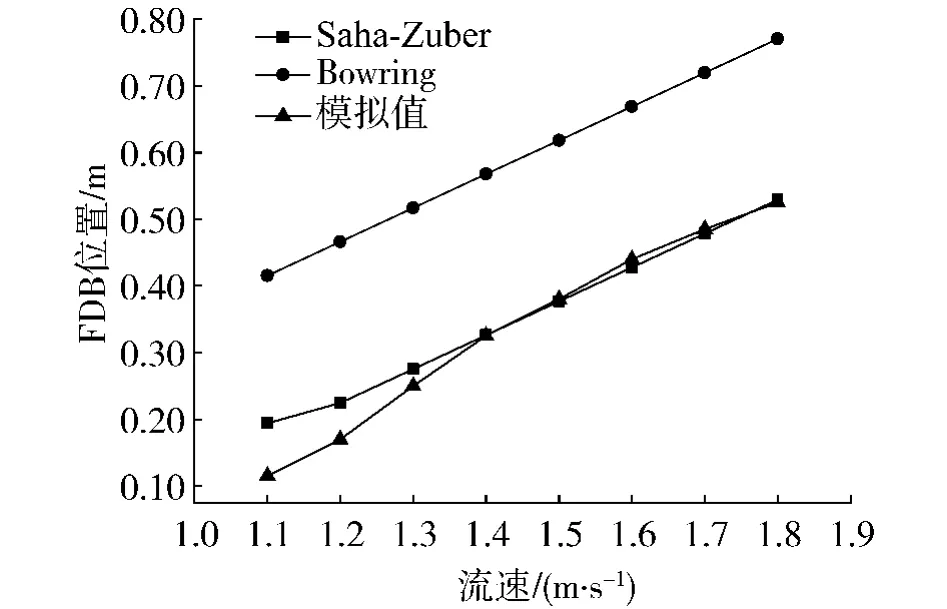
图1 圆管内模拟值与经典模型对比Fig.1 Comparison between simulation results and classicalmodels in circular tube
2.2 矩形通道内数值模拟值与经典模型对比
将建立的模型用于矩形通道,利用Fluent模拟矩形通道内常压下过冷沸腾气泡脱离点,并与经典模型进行对比.图2是过冷度为40℃、热流密度为250 kW/m2双面加热情况下的Fluent模拟值与经典模型计算值.

图2 矩形通道内模拟值与经典模型对比Fig.2 Comparison between simulation results and classicalmodels in rectangular channel
通过图2数值模拟结果与经典模型计算值的对比可以发现,两者达到了较好的吻合.在较广的功率范围内,模拟值介于Saha-Zuber模型和Bowring模型的计算值之间.
3 矩形通道实验研究
3.1 实验装置
实验回路如图3所示.工质首先由循环水泵泵出,经过流量计后进入预热器,在预热器内加热到预先设定的入口温度后,进入实验段,然后由直流电加热系统进行加热,加热后的工质进入冷凝器内冷却,最后流入循环水泵,这样便完成了整个回路的循环[4].
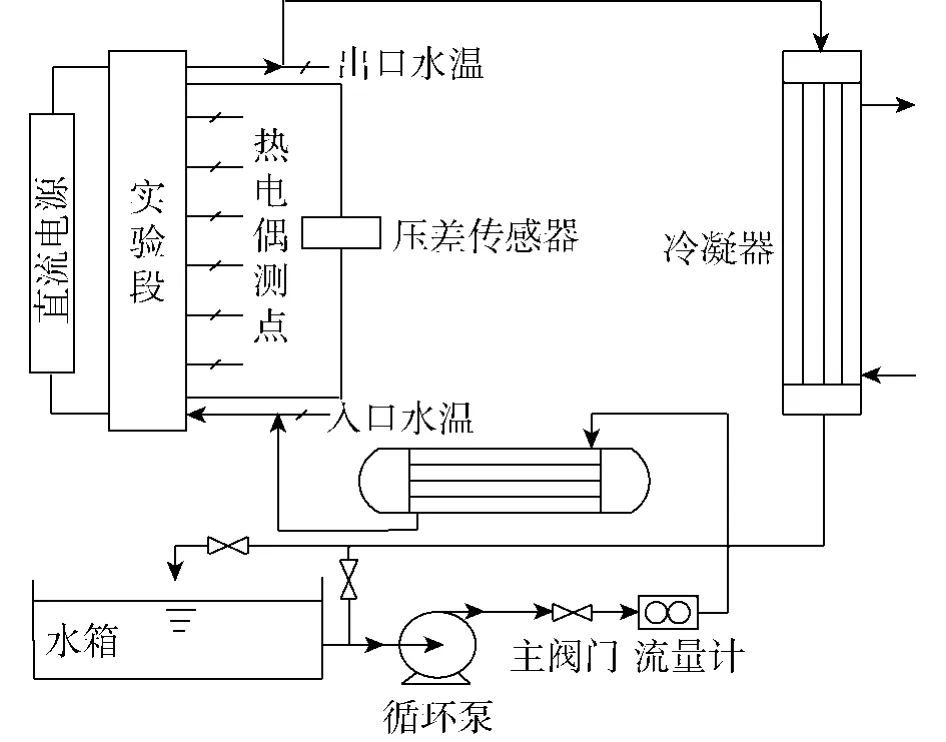
图3 实验回路示意Fig.3 Schematic diagramof experimental circuit
实验段是一个矩形通道,长1 m,横截面为40 mm×2 mm,壁面为不锈钢板,竖直安装,在其壁面上施加直流电加热.
3.2 气泡脱离点的判定
气泡脱离点的准确判定较为困难,研究者发展出多种判定方法[4].发生过冷沸腾时,由于换热系数的升高,会造成沿流动方向的壁温曲线变平甚至降低,因此通过寻找壁温的转折点可以确定过冷沸腾气泡脱离点.通过壁温确定FDB点的方法又可分为2种:
1)轴向壁温转折法:根据热电偶测得的壁温数据,绘制壁温的变化曲线,壁温曲线变平或者降低的转折点即为过冷沸腾气泡脱离点.该方法的优点是较准确,不受人为因素的影响,缺点是在热电偶间距较大时,过冷沸腾气泡脱离点可能不在热电偶位置处,而是在2个热电偶间,因此存在着一定的偏差.
2)单点壁温转折法:在相同的实验工况下,逐渐增加加热功率,绘制单个热电偶测得的壁温随加热功率变化的曲线,壁温变平或者降低的转折点就是过冷沸腾气泡脱离点.该方法优点是准确度高,缺点是需要进行一系列连续实验才能得到一个点,效率较低.
本文采用以轴向壁温转折法为主,同时利用单点壁温转折法测得点作为校验的方法进行实验,结果发现2种方法偏差不大.
4 模拟结果与实验结果对比
4.1 经典模型与实验结果对比
图4是实验值和经典模型结果的对比,实验过程中连续地增加功率而保持其他参数不变,在达到稳定状态后开始采集参数.由于实验系统压力调节能力有限,导致系统的压力略有升高,因此实验结果与恒压值条件下的结果相比有一定偏差.经典模型选用了目前
公认的Saha-Zuber模型和Bowring模型.

图4 实验值与经典模型对比Fig.4 Comparison between experimental data and classicalmodels
从实验值与经典模型的对比可以发现,实验值与经典模型达到了较好的吻合,大多数点偏差小于10 cm,相对误差小于20%.这说明Saha-Zuber模型和Bowring模型虽然源于圆管,但是适用于双面加热矩形通道,且具有较高的准确度.从图4上可以发现,在个别点处经典模型预测值与实验结果有较大的偏差,这主要是由在实验中过冷沸腾气泡脱离点的判断方法造成的.在实验中,根据由热电偶测得的壁温变化曲线确定过冷沸腾气泡脱离点,认为壁温变平或者下降的转折点为过冷沸腾气泡脱离点.但是由于实验段上的热电偶只有几个,热电偶的间距较大,不同工况下壁温转折点可能都在同一热电偶处,或者是转折不太明显,因此导致了位置的偏差.
4.2 数值模拟结果对比
利用 Fluent模拟在压力为1.2 MPa、流速为0.5 m/s时不同功率下双面加热矩形通道内过冷沸腾气泡脱离点,并与实验结果进行对比.图5为3组对比值,从左至右依次对应3个入口过冷度20℃、30℃和40℃.
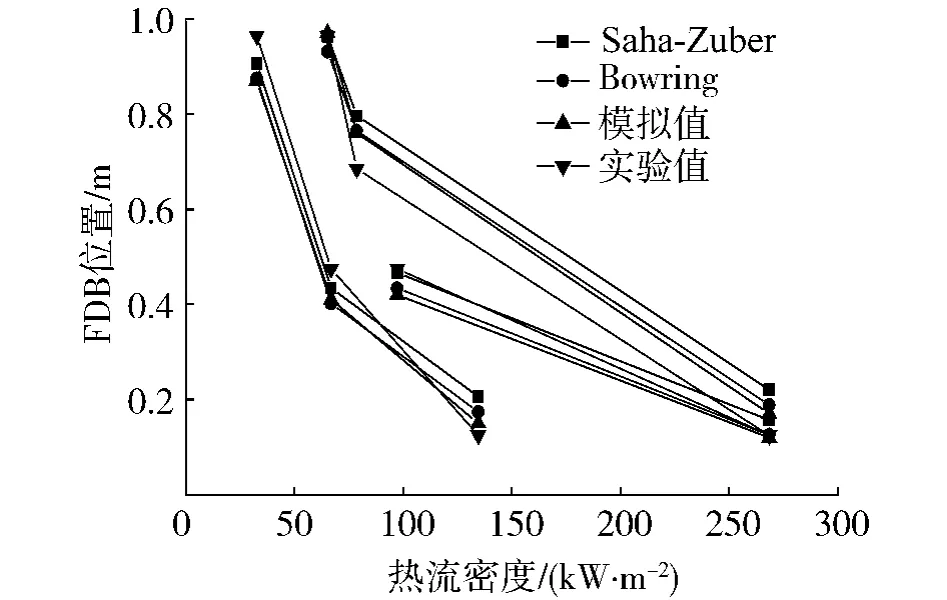
图5 矩形通道数值模拟值与实验值对比Fig.5 Comparison between simulation results and experimental results in rectangular channel
通过数值模拟值与实验值的对比发现,两者达到了较好的吻合,偏差一般小于10 cm.并且数值模拟值与Saha-Zuber模型和Bowring模型的计算值都很相近,说明了数值模拟确定矩形通道气泡脱离点的可行性、准确性.
5 结论
通过将气泡脱离点数值模拟结果与经典模型计算结果、实验结果进行对比,验证了数值模拟结果的准确性.通过分析,得到了以下结论:
1)提出的过冷沸腾气泡脱离点数值模拟的数学物理模型和方法可行,实现了通过数值模拟预测气泡脱离点位置.
2)数值模拟结果与经典公式以及实验值吻合良好,说明本文提出的模型是合理的.
3)数值模拟过冷沸腾气泡脱离点具有较高的准确度,平均偏差小于20%.
4)根据本文数值模拟的实践,对数值模拟预测过冷沸腾气泡脱离点,网格尺寸选为0.1 mm比较合适.这种尺寸模拟精度比较好的机理需要进一步分析.
5)源于圆管的Saha-Zuber模型和Bowring模型适用于双面加热矩形通道.
[1]阎昌琪.气液两相流[M].哈尔滨:哈尔滨工程大学出版社,2010:50-55.
[2]徐济鋆.沸腾传热和气液两相流[M].2版.北京:原子能出版社,2000:278-279,280-282
[3]周涛,杨瑞昌,刘若雷.自然循环欠热沸腾起始点特性[J].原子能科学技术,2006,40(2):172-176.ZHOU Tao,YANG Ruichang,LIU Ruolei.Characteristic of onset of nucleate boiling in natural circulation[J].Atomic Energy Science and Technology,2006,40(2):172-176.
[4]秦胜杰.摇摆对自然循环气泡脱离点影响的实验研究[D].哈尔滨:哈尔滨工程大学,2007.QIN Shengjie.Experimental study on bubble departure in natural circulation under rolling condition[J].Harbin:Harbin Engineering University,2007.
[5]SUN Qi,YANG Ruichang,ZHAO Hua.Predictive study of the incipient point of net vapor generation in low-flowsubcooled boiling[J].Nuclear Engineering and Design,2003,225(2/3):249-256.
[6]KURETA M,HIBIKIT,MISHIMA K,et al.Study on point of net vapor generation by neutron radiography in subcooled boiling flowalong narrowrectangular channels with short heated length[J].International Journal of Heat and Mass Transfer,2003,46(7):1171-1181.
[7]LIY,YEOH G H,TU JY.Numerical investigation of static flowinstability in a low-pressure subcooled boiling channel[J].Heat and Mass Transfer,2004,40(5):355-364.
[8]TU Jiyuan.On numerical modeling of lowpressure subcooled boiling flows[J].International Journal of Heat and Mass Transfer,2002,45(6):1197-1209.
[9]樊普,贾斗南,秋穗正.低压下水欠热流动沸腾的两相
CFD数值模拟研究[J].原子能科学技术,2011,45(4),412-420.FAN Pu,JIA Dounan,QIU Suizheng.CFD investigation of subcooled flowboiling model under lowpressure[J].A-tomic Energy Science and Technology,2011,45(4),412-420.
[10]BOSTIAN K,BORUT M.Modeling of low-pressure subcooled flowboiling using the RELAP5 code[J].Nuclear Engineering and Design,2003(220):255-273.
[11]ECKHARD K,ROLAND R.CFD for subcooled flowboiling:simulation of DEBORA experiments[J].Nuclear Engineering and Design,2011(241):3851-3866.
[12]韩占忠,王敬,兰小平.FLUENT流体工程仿真计算实例与应用[M].北京:北京理工大学出版社,2004:137-171.
