基于酉变换的虚拟阵列DOA估计算法
2012-09-02闫金山彭秀艳王咸鹏
闫金山,彭秀艳,王咸鹏
(哈尔滨工程大学 自动化学院,150001哈尔滨)
波达方向估计一直都是阵列信号处理的一个重要内容,在通信、雷达与声纳等领域都得到广泛应用.很多高分辨率子空间类算法比如MUSIC算法[1]和ESPRIT算法[2]在最近这些年得到了很大的发展.但这些算法都是在对接收数据协方差矩阵的特征值分解基础上进行,为了获得良好的估计性能,往往需要上百甚至上千的采样拍数.且在信源相干时,这些传统的子空间类算法性能会急骤下降,甚至失效,导致无法估计出信源的波达方向.
为了能够解决这些问题,很多学者针对相干信源提出相关的解相干技术.文献[3-4]分别提出了空间平滑算法和前后向空间平滑算法,实现了对相干信源的解相干,但由于空间平滑算法的解相干性能是以损失阵列孔径为代价的,因此在小采样拍数和低信噪比时估计性能急骤下降.文献[5-7]提出了基于数据重构的解相干算法,避免了阵列孔径的损失,提高了角度分辨率,获得了良好的估计性能,但由于重构数据需要庞大的计算量,不利于实时处理.文献[8]提出了一种矩阵束(Matrix pencil,MP)解相干算法,该算法避免了阵列孔径损失,且减少了一定的计算量,但该算法却只适用在高信噪比的信号环境.文献[9]提出了一种酉变换MUSIC的解相干算法(UMUSIC)能够在低拍数下实现相干信源的解相干,但估计性能不是很理想.
本文在虚拟阵列的基础上提出了用酉变换矩阵对阵列虚拟平移获得的虚拟阵列接收数据的协方差矩阵进行处理的方法,得到一个实数的协方差数据矩阵,利用该数据矩阵进行波达方向的估计.该算法不仅没有损失阵列,阵列分辨率也得到很大的提高,在低信噪比情况拥有很好的估计性能,而且在低采样拍数时能够得到正确的波达方向估计,计算量很小,可以进行实时处理.仿真结果表明该算法具有很好的解相干性能和良好的估计性能.
1 信号模型
图1给出由M个阵元组成的均匀等距线性阵列模型,阵元距为d.设有N个远场窄带相干或者非相干的信号以平面波形式从N个方向θi(i=1,2,3,…,n)入射到阵列中,则第k个阵元接收到的信号为
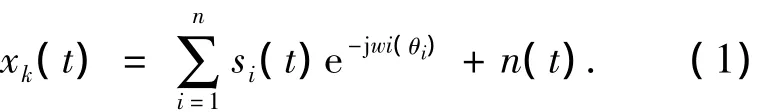
式中:si(t)为在空间参考点测量的第i个期望信号源的复信号包络形式,i(θi)为第i个期望信号相对于参考点的延迟时间,对于均匀等距阵列,i(θi)=(k-1)dsin(θi)/c,c为信号的传播速度;n(t)为零均值高斯白噪声.

图1 阵列信号模型
假设信号源与噪声之间互不相关,且噪声与噪声之间互不相关.那么阵列通道通过采样后接收数据的向量表示为
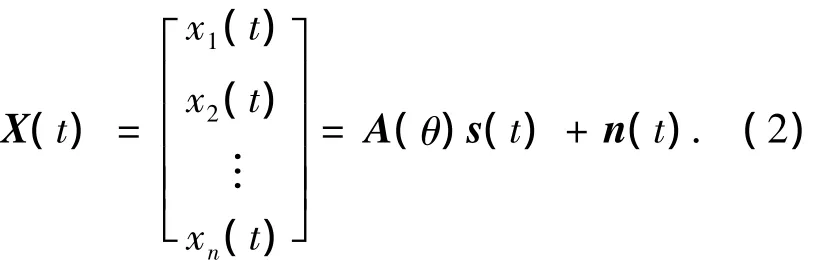
式中:A(θ)=[a(θ1),a(θ2),…,a(θn)]为M×N维期望信号的阵列方向矢量,s(t)=[s1(t),s2(t),Λ,sn(t)]T为N×1维期望信号矩阵,α(θi)=[1,e-jwi(θi),e-j2wi(θi),Λ,e-j(m-1)wi(θi)]T为M×1维的方向矢量,n(t)为M×1阵列接收到的噪声矩阵.
在阵列接收信号时,若信源之间为相干的,将会导致信号子空间的维数小于信号源数,即信号子空间的信息“扩散”到了噪声子空间,使某些相干信源的方向矢量与噪声子空间不是完全正交的,从而无法得到正确的估计.针对以上问题,本文提出一种基于酉变换的虚拟阵列DOA估计算法.
2 基于酉变换的虚拟阵列算法
虚拟阵列的目的就是通过虚拟平移构建1个满秩的接收数据协方差矩阵,使得期望信号的信息保存在信号子空间中,得到正确的估计结果.在文献[10]中已经证明对于N个相干信源,经过虚拟阵列平移后,只要满足虚拟阵列的数目L≥N,使协方差矩阵恢复满秩,就能实现相干信源的解相干.
如图2所示,阵列虚拟平移的基本原理就是每次将阵列等距地向右平移1个阵元的距离d每次平移形成1个新的阵列,第l(0≤l≤L)个虚拟阵列的接收信号表达为
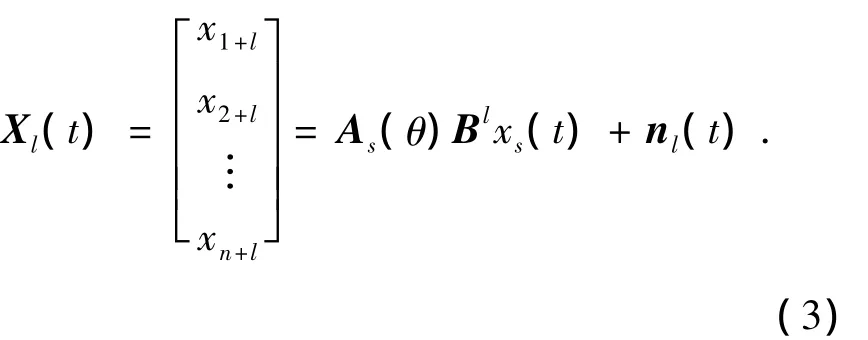
式中B=diag[exp(j2πdsin(θ1)/λ,exp(j2πdsin(θ2)/λ,…,exp(j2πdsin(θn)/λ]为维数为N×N的阵列虚拟平移变换矩阵.nl(t)为第l个虚拟阵列通道中接收的噪声.
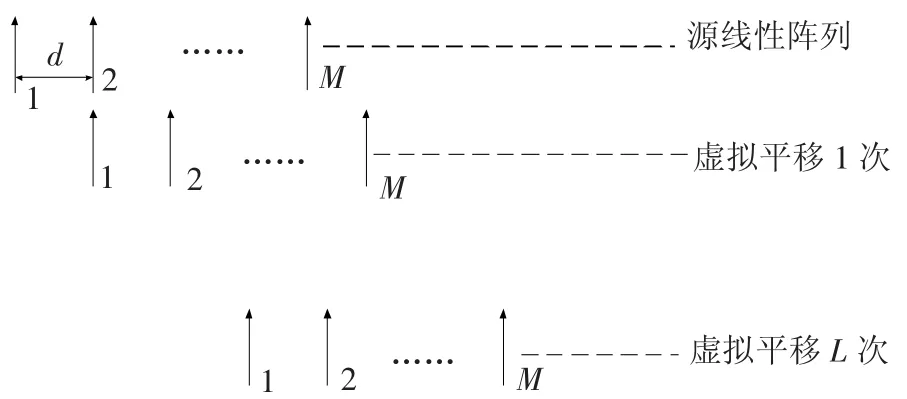
图2向右等阵元距虚拟平移形成虚拟阵列原理图
在单拍采样的情况下,L个虚拟阵列输出数据为维数N×(L+1)的矩阵,可表示为

定义一个反对角置换矩阵,在反对角线上元素全部为1,其余元素全部为0,表示为
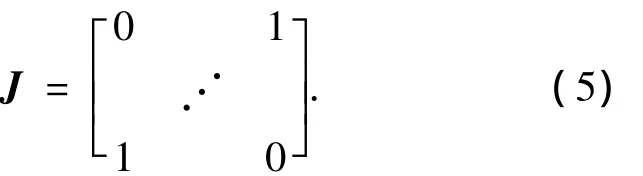
用反对角置换矩阵J重构阵列接收数据,得到一个包含更多信号信息的数据矩阵W,即

由数据矩阵W构成的协方差矩阵为
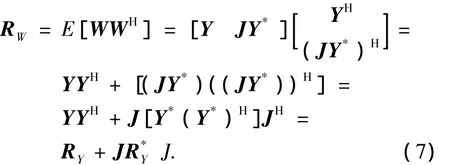
式中:J=JH,RY为虚拟阵列在单拍数采样下输出数据的协方差矩阵.
由式(5)、(7)可得
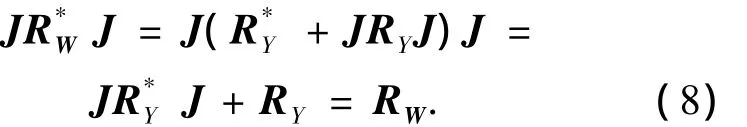
式(7)中所包含的数据都是在复数域里面,用MUSIC算法估计波达方向估计中,需要对协方差矩阵进行特征分解和波峰峰值搜索,在复数域里面需要进行大量的计算,若转换为实数域中进行,会减少大量计算复杂度.由于RW为Centro hermitian矩阵,因此可以定义1个维数为N×N的酉变换矩阵U,协方差矩阵RW经过酉变换后的实域协方差矩阵为

式(9)中当N为偶数时
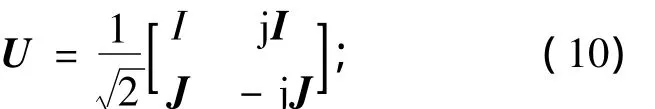
式(9)中当N为奇数时

在式(10)中,I和J分别为维数为[N/2]×[N/2]的单位矩阵和反对角置换矩阵.
在式(11)中,I和J分别为维数为[(N-1)/2]×[(N-1)/2]的单位矩阵和反对角矩阵,为维数1×[(N-1)/2]的全零行向量.且观察酉变换矩阵U可知,U=JU*.
结合式(7)、(8)可得
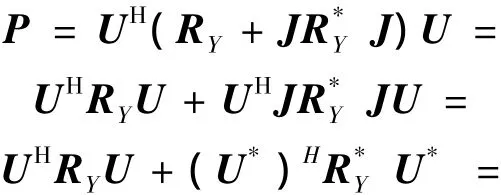

式(7)的数据协方差矩阵是在单拍采样下得到的,为了得到更好的性能,一般情况下都采用多拍采样.若采样总拍数为p次,则第i(i=1,2,…,p)次采样阵列输出的数据为
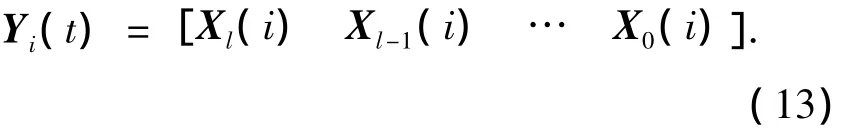
阵列输出的总数据为
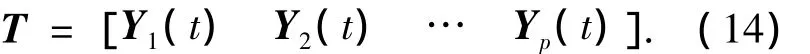
在本文的方法中,p取值较小,一般在10以下,这样更加有利于进行实时处理,利用式(6)可以得到多拍采样后包含更多信号量的数据矩阵H为
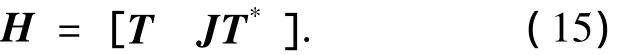
则接收数据的协方差矩阵

式中:RT为虚拟阵列在多拍数采样下输出数据的协方差矩阵,同理可知RH为Centro hermitian矩阵.
由式(9)、(16)可以得到多拍采样下的实数协方差矩阵

对多拍采样后得到的实值域协方差矩阵D进行特征值分解,得
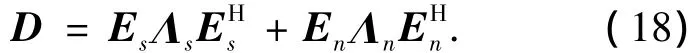
式中:Es=[e1,e2,…,en]为多拍采样下的实值协方差矩阵对应的信号子空间,即大特征值对应的特征向量组成的空间.En=[en+1,en+2,…,em]为多拍采样下的实值协方差矩阵对应的噪声子空间,即小特征值对应的特征向量组成的空间.Λs=diag[λ1,λ2,…,λn]为多拍采样下的实值协方差矩阵对应的信号特征值,即大的特征值.Λn=diag[λn+1,λn+2,…,λm]为多拍采样下的实值协方差矩阵对应的噪声特征值,即小的特征值.
文献[1]中MUSIC算法利用噪声空间与阵列方向矢量的正交性,构造出空间谱函数,然后通过搜索空间谱函数的峰值来确定信号的波达方向,本文采用类似的方法构造一个空间谱函数Pk(θ),即
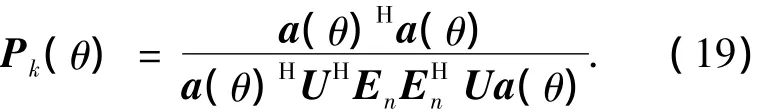
式中:En为式(18)中对应的噪声空间,a(θ)为阵列的搜索方向矢量,可以通过搜索空间谱函数Pk(θ)的峰值得到相干信源的波达方向.这里采用了MUSIC算法估计信源波达方向,也可以采用求根MUSIC算法估计信源波达方向.
3 仿真及性能分析
为了验证算法的解相干性能和估计性能,这里将本文算法和文献[9]中提出的UMUSIC算法以及文献[4]中的前后向空间平滑(FBSS)算法进行比较.
3.1 算法估计特性的仿真比较
试验条件:阵列为均匀等间距的线阵阵列,阵元距为半个波长,阵元数为8,2个相干信源分别从-20°和20°入射到阵列中,信噪比均为0dB,采样拍数为20和2.
图3、4分别给出了采样拍数为20和2情况下,本文算法和UMUSIC算法的仿真性能对比.可以看出,在采样拍数为20时,本文算法和UMUSIC算法均能很好的对相干信源进行解相干,能够准确地估计出相干信源的波达方向.但在采样拍数为2时,UMUSIC方法在估计相干信源波达方向时已经出现了干扰的波峰,从而影响估计信源波达方向的精度,这主要是由于UMUISC算法是通过前后向空间平滑解相干,损失了阵列孔径,估计精度低,低拍数采样时更加容易受到噪声干扰,出现了伪峰,影响估计结果.本文方法能够精确地估计出相干信源的波达方向,而且在相干信源的方位形成尖锐的波峰,信源方位之间的谱线幅度压低至接近0 dB.因此本文的方法具有更高的分辨率,能够在低采样拍数下准确估计出相干信源的波达方向.
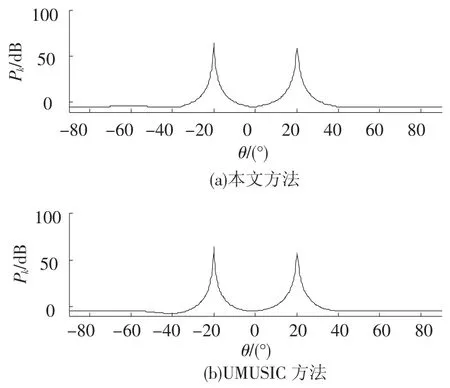
图3 采样拍数为20时估计性能比较
3.2 算法统计特性的比较
在2个相干信源的条件下,比较本文方法和UMUSIC算法、FBSS算法的统计性能.8个阵元的均匀等距线性阵列接收2个方位为-10°和20°的相干信源,采样拍数为2,仿真结果为对每个SNR点做500次蒙特卡洛仿真的统计结果.图5和图6分别给出了3种算法的均方根误差和估计成功概率的性能比较.
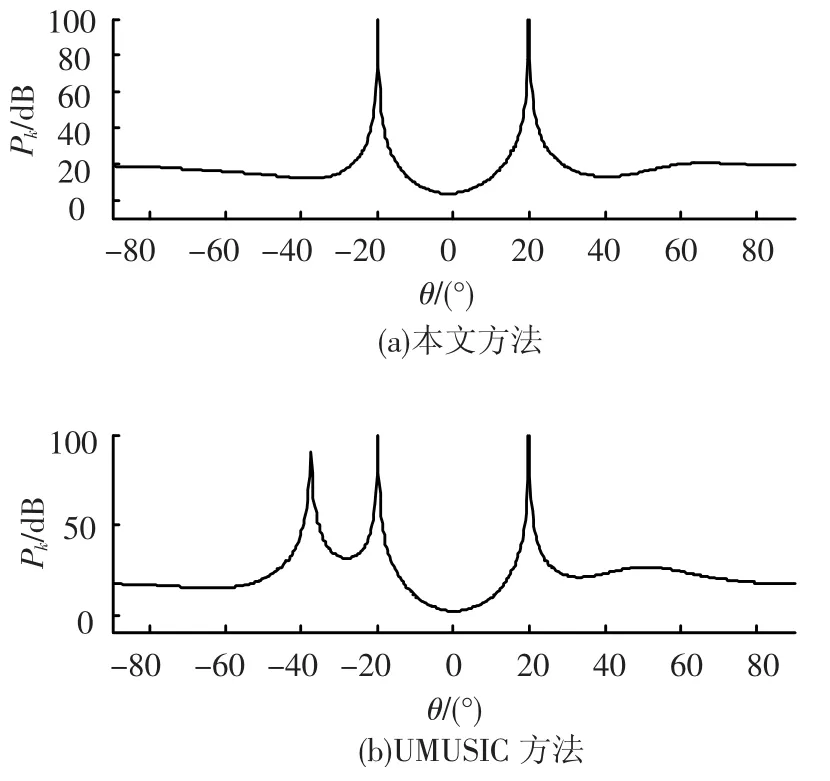
图4 采样拍数为2 时估计性能比较
图5给出了不同信噪比情况下,3种算法的估计均方根误差的比较曲线.由图中可以看出,无论是在低信噪比还是在高信噪比环境中,FBSS方法和UMUSIC算法的估计均方根误差基本一致,但均比本文方法的均方误差要大很多,估计性能不是很理想.而本文方法在信噪比RSN为5 dB时,估计均方根误差已经很小,估计性能明显优越于FBSS方法和UMUSIC算法.
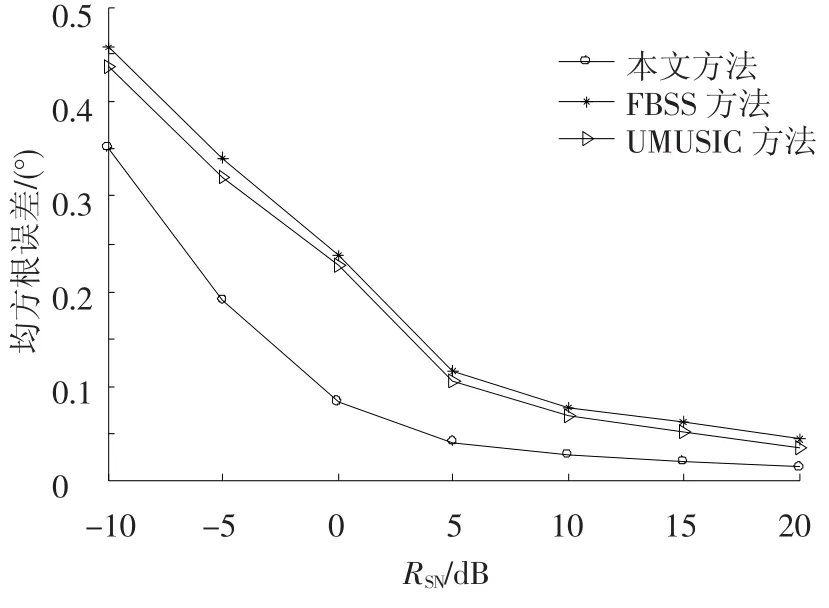
图5 均方根误差比较曲线
图6给出了不同信噪比情况下,3种算法的估计成功概率比较曲线.从图中可知,本文的方法在估计成功概率方面拥有低的信噪比门限,在信噪比为5 dB时估计成功概率达到100%,而FBSS算法和UMUSIC方法在大约13 dB时估计成功概率才能达到100%,因此本文方法能够在较低的信噪比情况下准确地判断出相干信源的波达方向.
由于FBSS方法和UMUSIC的解相干是以损失阵列孔径为代价的,在阵元数目较少的情况下,估计性能和分辨力都会受到很大的影响.而本文方法不损失阵列孔径实现了对相干信源的解相干,具有很低的信噪比门限以及较小的均方根误差和估计方差,因而本文算法在低信噪比环境下具有更好的解相干性能.
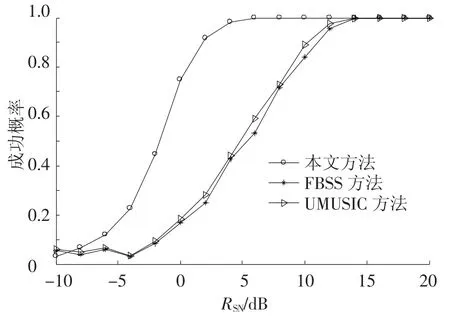
图6 估计成功概率比较曲线
4 结论
1)提出了基于酉变换的虚拟阵列DOA估计算法,该方法不仅避免了空间平滑类解相干算法损失的阵列孔径,而且减少了重构矩阵解相干的计算复杂度.
2)基于酉变换的虚拟阵列DOA估计算法在较少的拍数和不损失阵列孔径情况下可有效估计出相干信源的波达方向,运算量小,有利于实时处理,是一种较好的解相干算法.理论分析和仿真结果验证了该算法的有效性.
[1]SCHMIDT R O.A signal subspace approach to multiple emitter location and spectral estimation[D].California:Stanford University,1981.
[2]ROY R,KAILATH T.ESPRIT-estimation of signal parameters via rotational invariance techniques[J].IEEE Trans on ASSP,1989,37(7):984-995.
[3]SHAN T J,WAX M,KAILATH T.On spatial smoothing for direction of arrival estimation of coherent signals[J].IEEE Trans Acoust Speech Signal Process,1985,33(4):806-811.
[4]PILLAI S U,KWON B H.Forward/backward spatial smoothing techniques for coherent signal identification[J].IEEE Trans Acoust Speech Signal Process,1989,37(1):8-15.
[5]LIU Fuguang,DIAO Ming.A novel algorithm for DOA estimation[C]//Second International Symposium on Information Science and Engineering.Shanghai:IEEE,2009:488-492.
[6]BAI Jun,SHEN Xiaohong,WANG Haiyan,et al.Improved Toeplitz algorithms to coherent sources DOA estimation[C]//International Conference on Measuring Technology and Mechatronics Automation.Changsha:IEEE,2010:442-445.
[7]YE Zhongfu,XU Xu.DOA estimation by exploiting the symmetric configuration of uniform linear array[J].IEEE Transactions on Antennas and Propagation,2007,55(12):3716-3720.
[8]YILMAZER N,KOH J,SARKAR T K.Utilization of a unitary transform for efficient computation in the matrix pencil method to find the direction of arrival[J].IEEE Transactions on Antennas and Propagation,2006,54:175-181.
[9]TAYEM N,POUR M N.A unitary music-like algorithm for coherent sources[C]//IEEE Vehicular Technology Conference.Baltimore:Institute of Electrical and Electronics Engineers Inc.,2007:551-555.
[10]张陆游,张永顺,杨云.基于阵列虚拟平移快速解相干幂代算法[J].系统工程与电子技术,2010,32(2):252-255.
