超音速反舰导弹拦截策略仿真*

钱占进，刘家祺，欧阳中辉，于嘉晖

(1.解放军91492部队，山东 青岛 266001;2.海军航空工程学院，山东 烟台 264001)

目前舰空导弹按射程可划分为远程(射程超过100km)、中程(射程 20km-100km)、近程(射程 10km-20km)和末端(射程不超过10km)四个层次，拦截的目标主要有低空飞行的飞机和反舰导弹，其中末端能进行机动的超音速反舰导弹速度快、过载大，留给火控系统的反应时间短，给准确拦截造成了很大的困难。

分析制导控制系统精度的主要方法［1］有蒙特卡洛法、协方差分析法和统计线性化伴随法等。协方差分析法和统计线性化伴随法现在已经发展得比较成熟，只需计算一次就可以达到足够的精度，但是导弹的制导控制系统是变系数非线性的，其线性化过程中存在方法误差，且理论推导过程复杂［2］。蒙特卡洛法可以对导弹整个工作过程进行全方位的模拟，因此可信度高，可以作为其他方法的验证，不足之处是计算量大，需要经过多次仿真计算才能达到令人满意的精度，计算机技术的飞速发展很好地解决了这个问题［3-4］。本文在三维弹道仿真的基础上，采用蒙特卡洛法实验法分析了反舰导弹对超音速反舰导弹的拦截情况。

1 舰空导弹三维矢量拦截模型

地面坐标系(Oxyz)d与地球固连，以导弹发射时刻舰空导弹质心在地面的投影点为原点Od，xd轴在水平面内，指向目标方向为正;yd轴沿铅垂线向上为正;zd轴与其他两轴垂直并构成右手坐标系，如图1所示。

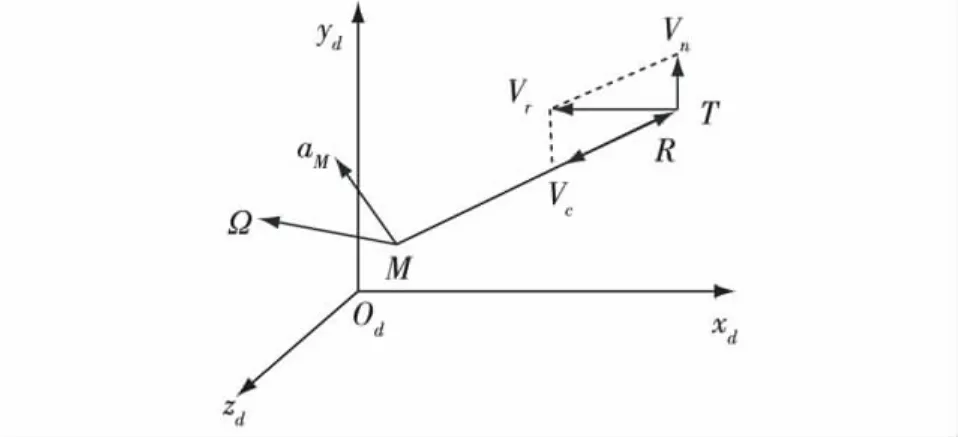
图1 地面坐标系

反舰导弹和舰空导弹的速度分别为VT和VM，目标对于舰空导弹的相对速度矢量Vr=VT-VM，Vr在R方向的投影分量Vc，在R的垂直方向的投影分量为Vn。矢量R的转动角速度为Ω，舰空导弹的指令加速度aM。

设反舰导弹质量为m，动量为P=mVr，相对于原点Or的角动量为L，用速度表示:

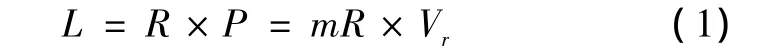
其相对于原点的转动惯量为I，矢量R的转动角速度为Ω，根据转动惯量定义I=mR2，则角动量L用角速度表示:

由式(1)和式(2)得，mR×Vr=mR2Ω，则Ω的矢量计算公式为

Vc方向与R平行，方向相反，所以有

由相对速度平行方向分解公式|Vc|=|Vr||cosθ|和点积定义式得

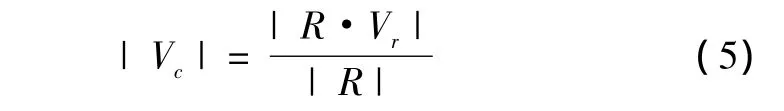
将式(5)代入式(4)，得

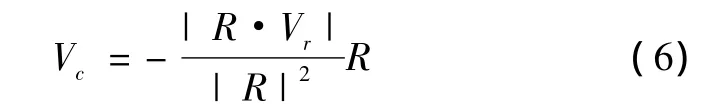
真比例导引律(TPN)的指令加速度aM施加在垂直于视线的方向，其大小正比于接近速度Vc大小和视线角速率|Ω|的乘积［5-6］，即

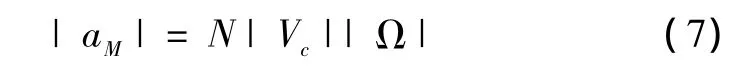
由右手螺旋定则知Ω垂直于视线转移平面内的矢量aM和Vc，TPN中aM垂直Vc，所以导引律矢量形式为

将式(3)、式(6)代入导引方程(8)，得

弹目相向运动时R·Vr的符号一直都是负的，去掉绝对值符号后，方程为

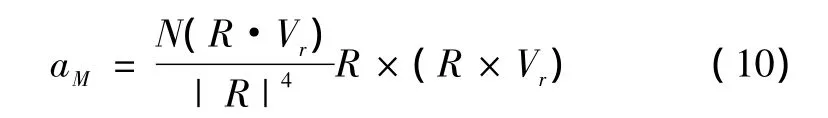
理想情况下，视线角速度只是由相对运动产生的，事实上它还受进入导引头闪烁噪声、接收机噪声和角噪声等大量干扰因素的影响，由中心极限定理知，满足一定条件下大量随机变量和的极限是高斯分布的［7］，所以可以合理假设导引头输出量视线角速率上存在一个符合N(ξ，σ2)高斯噪声x，视线角速度的方向仍然不变。则有:

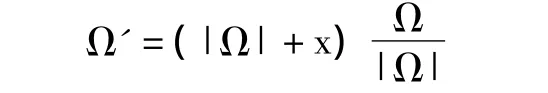
加速度受弹体操作力矩的限制，不一定能满足上述指令加速度的要求，实际作用于弹体的加速度

其中，amax为弹体最大可用过载。

若已知舰空导弹的初始位移和速度和目标的运动方程，可以通过数值积分的方法计算出任意时刻舰空导弹的运动状态，从而得到舰空导弹的拦截弹道以及拦截过载和脱靶量等参数。

2 反舰导弹三维矢量模型

为了提高反舰导弹的突防概率，现代反舰导弹高速机动等飞行性能得到了大幅提升，大多采用末端或全程超音速超低空掠海飞行，预设或者随机改变飞行高度，方位发射和蛇形机动等改变飞行方位，末端跃升俯冲等方式攻击水面舰艇的水线要害部位。现代反舰导弹的弹道主要可分为发射段，巡航段，机动段，比例导引段，跃升俯冲段［8］五个阶段。典型弹道如图2所示。

图2 反舰导弹典型弹道

发射段大多离目标距离很远，防空武器系统很难在这么短的时间内对其进行拦截，因此研究意义不大。下面分阶段建立反舰导弹的三维弹道模型。

2.1 巡航段模型

巡航段距离舰艇目标在20km以上，属于中远程舰空导弹的防空范围。除了航迹规划点外，大多时间没有机动，所以可以简化为VC(匀速运动)模型。取A点为弹道起始点，此时t=0，巡航段(AB)初始位移A=(xA，yA，zA)，速度 VA=(vAx，vAy，vAz)，则 t时刻反舰导弹的位移 T=(xT，yT，zT)，速度 VT=(vTx，vTy，vTz)，则有:

2.2 机动段模型

距离舰艇小于20km时，反舰导弹已经进入近程防空范围，这个阶段被击落的概率很大，所以机动开始时机大多在这个阶段，目前超音速反舰导弹大多采用蛇形机动技术。开始蛇形机动后，通过舵偏指令控制导弹飞行，主要体现为航向角和水平面法向加速度的反复变化，机动的程度受到最大侧向过载的限制。为了方便计算，假设其在水平面内做轴线平行于坐标轴的正弦曲线运动，周期为Ts，振幅为As，且保持不变。机动开始和结束时刻导弹速度都平行于坐标轴。

机动段(BC)开始时刻t=tB，导弹在B点，位移B=(xB，yB，zB)，假设在B点导弹平行于x轴飞行，若导弹速度仍为 VB=(vBx，vBy，vBz)，vBy=0，vBz=0，机动段任意t时刻反舰导弹的位移和速度分别为T=(xT，yT，zT)和 VT=(vTx，vTy，vTz)，则有

2.3 比例导引段模型

若反舰导弹已经突破前面远程和近程两层防空系统的拦截，到达距离舰艇小于10km的区域，对于被攻击的舰艇来说，只剩下最后一道防线，即由短程舰空导弹和速射炮组成的末端防御系统，为保证自身拦截成功率，一般先发射导弹拦截，若拦截失败，火控系统则把任务转交给速射炮。这段距离内，为保证自身命中率，反舰导弹往往采用比例导引方式修正前期由于机动造成的弹道偏差，由于超音速反舰导弹速度远大于舰艇，所以此段是相对比较平滑的弧形弹道。

比例导引段(CJ)开始时刻t=tC，反舰导弹位移和速度分别为 C=(xC，yC，zC)，VC=(vCx，vCy，vCz)，若此时舰艇位于H点，舰艇的位移和速度分别为H=(xH，yH，zH)，VH=(vHx，vHy，vHz)，假设舰艇目标不做机动，任意时刻t其位移和速度分别为

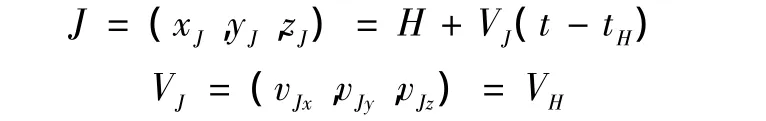
把式(10)中R和Vr换成舰艇相对反舰导弹的相对位移和相对速度，aM则为反舰导弹的指令加速度，同样可以通过数值积分方法计算反舰导弹的弹道。

2.4 跃升俯冲段模型

跃升俯冲大多在距离目标2km-4km处开始，简化俯冲段的机动模型为一作用在反舰导弹上的垂直向上的恒定过载aup，作用开始时刻t=tD，此时反舰导弹位于D点，其位移和速度分别为D=(xD，yD，zD)，VD=(vDx，vDy，vDz)为避免冲突，跃升过程撤消导引指令加速度的作用，跃升作用时间很短的时间tup后，恢复比例导引律的作用，此后由于惯性继续爬升到最高点后导弹开始俯冲攻击，俯冲角度取决于弹道最高点P和命中点Q，即以P为起点Q为终点的矢量RPQ与其在水平面投影的夹角。

爬升段弹道模型为:

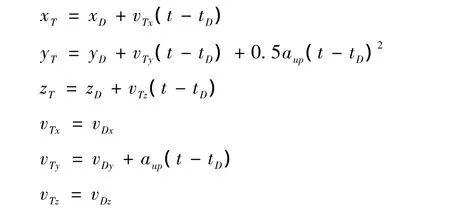
爬升段结束后，反舰导弹弹道仍为比例导引律作用下的弹道，上文中的比例导引段模型仍然适用，通过此模型解得弹道的最高点P和命中点Q后，Q点坐标减去P点得到Q相对于P的位移矢量RPQ=(xPQ，yPQ，zPQ)，由该矢量求的俯冲角为

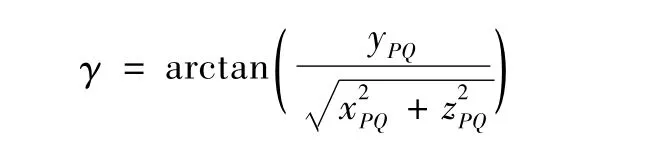
3 仿真分析

仿真步长取0.01s，有效导航比N=4。在地面坐标系中，巡航段超音速反舰导弹沿x轴负方向作匀速直线运动，被攻击的舰艇沿着z轴正方向作匀速直线运动，初始时刻t=0，反舰导弹和舰艇分别在A点和E点，反舰导弹四个阶段起始点在A，B，C，D点，对应时刻舰艇在E，F，G，H点，舰空导弹发射点也选择在各机动段的开始时刻，所以，E，F，G，H点也是舰空导弹的发射点。

反舰导弹T在A，B，C，D点的初始位移和速度:

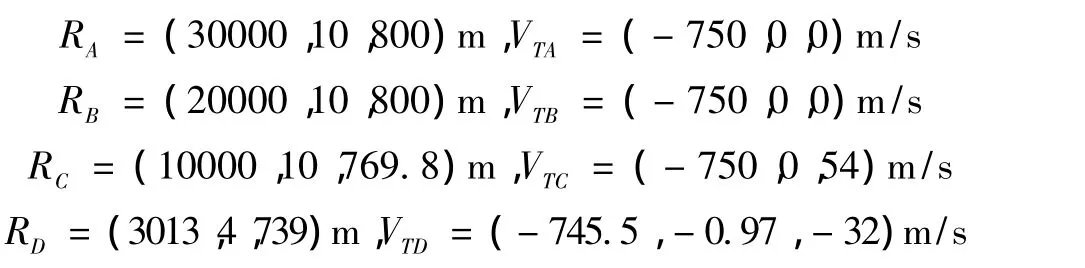
舰艇J在E，F，G，H点的初始位移和速度:

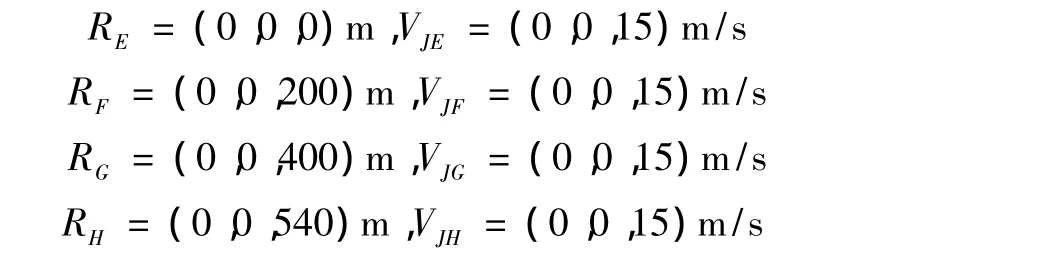
舰空导弹M在E，F，G，H点的初始位移和速度:

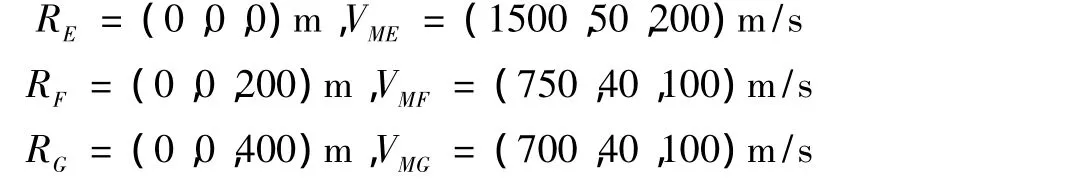
以上初始条件的设置充分考虑到了反舰导弹各个阶段弹道的平滑衔接，同时也考虑到远程和近程舰空导弹拦截速度的差异，通过Matlab仿真得到了反舰导弹机动段以蛇形机动为例的完整弹道以及舰空导弹在四个阶段的拦截弹道，如图3所示。

图3 四个阶段的拦截弹道

图4-7分别为各个阶段舰空导弹的需用过载曲线，左图为需用加速度矢量在三个坐标轴分量图，右图为其标量值变化曲线。反舰导弹蛇形机动段的机动幅度和周期为As=20m，Ts=2s，最大机动过载asmax=20g。由于受自身命中精度限制跃升俯冲机动过载不能太大，设跃升过载aup=10g，作用时间1s后按比例制导律俯冲攻击，俯冲过程中最大过载adn=15g。比较四个阶段的拦截需用过载曲线，巡航段最大拦截需用过载小于2g，比例导引段的拦截需用过载在3g以下，远小于其它段，巡航段过载单调减小，比例导引段稍有波动后总趋势减小，所以巡航段和比例导引段的拦截需用过载大小是收敛的。跃升俯冲段由于本身过载比机动段小，所以引起的拦截需用过载的最大值也稍小于机动段，但其大小在短短2s内发生了剧烈抖动，这说明末端跃升俯冲机动的拦截难度也很大。

舰空导弹过载限制为30g，为了便于比较，反舰导弹机动段和跃升俯冲段的最大过载都设定为20g，干扰噪声的均值和标准差相等，蒙特卡洛法仿真400次得到不同噪声强度下舰空导弹的脱靶量，其均值和方差为 d，σd，见表 1，表中第一行数字 1，2，3，4 分别代表反舰导弹的巡航段、机动段、比例导引段和跃升俯冲段。

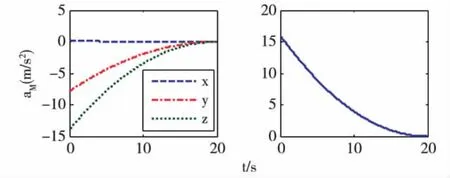
图4 舰空导弹拦截巡航段需用加速度

图5 舰空导弹拦截蛇形机动段需用加速度

图6 舰空导弹拦截比例导引段需用加速度

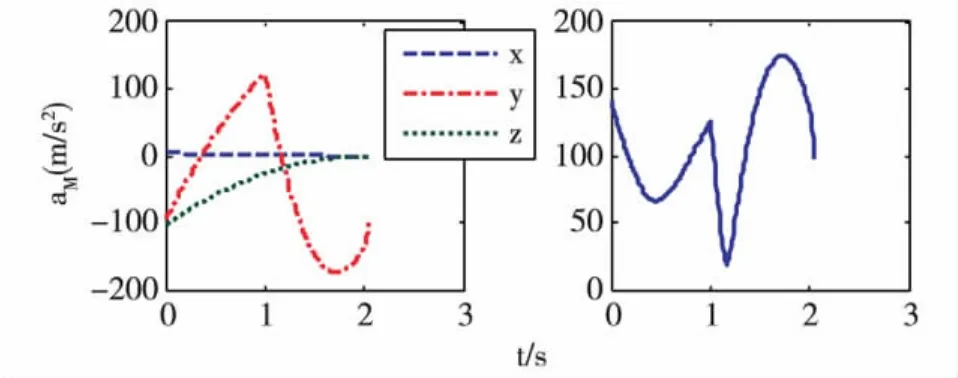
图7 舰空导弹拦截跃升俯冲段需用加速度

表1 舰空导弹脱靶量

通过上表的数据，可以得出以下结果:

1)比较前三个阶段脱靶量特征。在相同的干扰噪声作用下，反舰导弹拦截机动段脱靶量均值比比例导引段大，比例导引段脱靶量均值又比巡航段大。但是从脱靶量的方差角度看，机动段和巡航段没有太大差别，而比例导引段却远大于前面两个阶段。

2)比较第二段(机动段)和第四段(跃升俯冲段)的脱靶量特征。由于第四段反舰导弹和舰空导弹距离很近，所以相同强度的外部干扰体现在导引头输出上的噪声值要大于第二段，脱靶量均值相同的情况下，第四段的脱靶量方差远大于第二段，也就是说跃升俯冲段的命中点更为分散。

4 结束语

综合超音速反舰导弹四个阶段对舰空导弹的过载性能要求和脱靶量仿真结果，舰空导弹拦截处于机动段和跃升俯冲段时的反舰导弹难度较大，其次是比例导引段，最后是巡航段。舰空导弹应该尽可能在比例导引段和巡航段进行拦截以增大拦截成功率，拦截巡航段目标需要尽早地发现并跟踪目标，系统反应时间足够小保证在其机动前将其击毁。拦截比例导引段目标难点在于把握其蛇形机动终止时刻和跃升俯冲机动的开始时刻，在这两个时刻之间拦截效果较好。

［1］赵善友.防空导弹武器寻的制导控制系统设计［M］.北京:宇航出版社，1992.

［2］韩松臣.导弹武器系统效能分析的随机理论方法［M］.北京:国防工业出版社，2001.

［3］丁赤飙，毛士艺.采用修正比例导引的雷达寻的导弹脱靶量研究［J］.北京航空航天大学学报，1998，24(1):5-8.

［4］张安，何胜强，张耀中.飞机空面精确打击武器火控系统精度仿真分析［J］.系统仿真学报，2007，19(7):1569-1573.

［5］George M.Siouris.Missile Guidance and Control System［M］.New York:Springer-Verlag Inc，2004，168-173.

［6］杨军.导弹控制原理［M］.北京:国防工业出版社，2010.

［7］陆大琻.随机过程及其应用［M］.北京:清华大学出版社，1986.

［8］徐国亮，张逊，王勇.高速机动反舰导弹防御技术［J］.指挥控制与仿真，2011，33(1):1-5.