基于复杂网络理论的防空体系反飞机能力分析

王 伟，单连平，吴 奎

(江苏自动化研究所，江苏 连云港 222006)

复杂网络是复杂性理论研究的热点，是描述复杂系统内部结构的一种新手段，在数理科学、生命科学、社会科学、技术科学和管理科学等众多学科领域［1-2］得到了广泛应用。将复杂网络理论应用到战争系统的研究也是当前军事研究的热点［3-4］。

随着信息技术的飞速发展，现代战争的形态特征发生了极大的变化。作战的主要表现形式为网络中心战，区别于以往的平台中心战，网络战的特点在于将战场各个作战单元的网络化，把信息优势转变为作战行动优势，使得分散配置的部队共同感知战场态势，从而协调行动，以发挥最大效能。集成各种防空作战资源，实现防空体系内各作战要素之间的信息共享和综合运用，形成一个体系配套且多作战协同的网络化防空体系，具有结构、功能上的复杂性，就是一类复杂网络。为应对这种复杂性的挑战，需要使用复杂性理论对网络化防空作战进行理论指导。

本文试图运用复杂网络理论研究防空体系内部组织结构，以飞机编队的突防概率为防空体系反飞机能力的衡量标准，研究飞机编队对不同网络特征的防空体系的突防概率，以及这些网络特征参量对防空体系能力的影响，获得相关的结果，对体系的构建提供有益的参考。

1 复杂网络理论

1.1 复杂网络概述

复杂网络将复杂性和网络有机结合起来，通过物理统计、模拟仿真和动力学演化等途径来挖掘复杂大系统中的本质特征，它的发展经历了随机模型、小世界模型和无尺度网络模型。随机(ER)网络是由Erdos引入的，是概率方法与传统图论相结合的网络，着重于网络的随机性。经研究发现，大量的真实系统的网络模型既不是随机网络，也不是规则网络，而是介于随机网络和规则网络之间的复杂网络。1998年，Watts和Strogatz指出大量真实网络都具有小世界效应［5］;1999年，Barabasi和Albert指出许多现实世界中的大量网络具有无标度网络(scale-flee)的特性、无尺度特征、脆弱性和抗毁性［6］。

1.2 描述网络特性的特征量

1)度(Degree):一个节点的度定义为该节点连接其它节点的数目。在作战网络中，一个节点的度值往往反映了它的重要程度，比如指挥所所映射的节点一般具有较高的度值。

2)聚类系数(Clustering Coefficient):节点i的聚类系数定义为所有与节点i相邻节点之间连边的数目占可能的最大连边数目的比例。

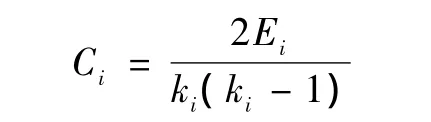
式中，Ei为实际存在的边数，ki为i的相邻节点个数。网络聚类系数C是网络中所有节点聚类系数的平均值。在作战网络中，聚类系数往往有2个方面的含义:表示在完成某个作战任务时，同一个作战单元内各个节点之间可以相互协调的能力;在网络的重建中有着重要意义，例如，作战网络在遭受敌方的打击时失去了与一些作战单元的联系，而聚类系数较高作战单元可通过其中任意节点与网络重要节点取得联系而有效完成网络重建。

3)平均路径长度(CPL):定义为网络任意两个节点间距离的平均值，即:

式中，dij定义为节点i和j之间的距离，指连接这两个节点的最短路径上的边数。作战网络的CPL值表示了网络传递信息的能力。信息时代的战争中，网络中节点间的距离即为两个作战单元进行通信控制所需要的跳数。平均路径长度在网络中扮演着重要的角色:平均路径长度越大，说明网络层次越多，网络中信息的流动、共享和同步将会越困难。

2 基于复杂网络理论的防空体系模型

防空体系是由预警探测系统、指控系统、拦截打击系统组成的反敌空中袭击的作战体系［7］。预警探测系统由空中预警、地面警戒雷达、无线电侦察等分系统及情报传递设备组成;指挥控制系统由各级指挥所及其所控制的引导、制导雷达，电子计算机和通信设备组成;拦截打击系统由歼敌机、地空导弹、高炮和电子设备等组成。

根据防空体系的定义，假设防空体系的构成如下:①一个旅级指挥所;② 三个防空导弹营指挥所，两个雷达营指挥所;③每个防空导弹营指控中心配置三个防空导弹火力连，每个雷达营配置两个预警雷达连。

根据体系的网络化程度建立五种防空体系的网络模型，如图1所示，所建立的网络类型为有权无向网络，节点的权值为该节点信息处理时间，边权值为该边的信息传递时间。节点1代表旅级指挥所，节点2-6为营指，7-15为导弹火力连(火力单元)，16-19为预警雷达连，网络的边代表通信、指控、协同等关系。

图1 防空体系网络模型

模型一:传统的指挥结构如图1中第一个模型所示，完整的作战过程要经历雷达、雷达营指挥所、旅指、营指挥所、火力单元。

模型二:在模型一的基础上，营指之间实现横向互连且所属同一个营的火力单元之间也完全互连的。这样缩短了指挥的流程，增加了体系的小集团特性。

模型三:在模型二的基础上增加了接替指挥关系且实现了雷达指挥所与火力单元完全互连。

模型四:在模型三的基础上，底层的火力单元与预警雷达连以50%概率相连。50%的连接概率理论上的作战效果与底层完全互连相差不会太大，但实际效果有待仿真检验。

模型五:底层单元实现完全互连。这时，体系的抗毁性将最强;同时，开销过大，结构也过于冗余。

设定指控节点的权值相同，代表处理时间为T，边权值如表1所示，单位权值表示信息传递时间为t。

表1 各节点对之间的权值

3 飞机编队突防效果的数学模型

首先，定义飞机编队突防概率QN:成功突防飞机数量占飞机总量的百分比，如果要求全部突防或者至少n架突防，计算全部或者至少n架突防成功的概率。

3.1 飞机编队突破拦截打击系统的数学模型

1)计算一次射击的击毁率

用导弹射击时，导弹单发命中率为P命中，武器单位能连射或齐射弹数m，则一次射击的命中率为

2)计算一个火力单位射击成功的概率

防空体系的工作流程特点决定了火力单位射击的成功率不仅取决于平台本身对目标的击毁概率P击毁，还与预警系统的发现概率P发现、指控系统正确指挥的概率P指挥、系统工作可靠的概率P可靠有关，一个火力单位射击成功的概率W'是这些概率乘积的结果。

为火力半径，t射击(s)为每次射击需要的时间，V(km/h)为突防飞机速度。

3)计算高射兵器射击架次数和平均射击架次数

a)由飞机编队长L(m)，高射兵器的射击周期T周(s)，火力单位数n可以计算出可能射击架次数n'。

当一个火力单位可以射击k个目标，上式变为:

b)平均射击的架次数(n'平均)

由突防距离D(km)、防区总面积S总(km2)、兵器总数量n总、编队宽I(km)可以计算整个拦截系统能射击的架次数n'平均，其计算公式为:

4)计算突防平均百分数

由式(2)和式(5)可以得到N架飞机组成的编队的突防概率QN:

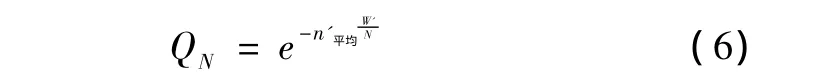
3.2 预警、指控系统对飞机突防概率的影响

预警、指控系统对飞机突防概率的影响反映在能否在最短的时间内以最高的准确概率把命令传送到拦截打击系统，让拦截打击系统有充分的时间对突防飞机进行拦截。在已有的飞机突防概率的模型中，与其他参数为固定值不同，参数突防距离D与预警、指控系统对拦截打击系统的支持程度有关，也就是与反应时间Δt相关。Δt在一定范围内时，火力系统能够实现尽远拦截;随着Δt的增大，指控信息不能及时地送到火力单位，飞机的突防距离将减小;Δt大到一定程度，系统将对飞机编队不能反应，编队将成功突防。

下面将通过数学模型分析指控系统对飞机突防概率的影响。

1)最近拦截的预警时间需求

最小预警时间:tyj=tfy+tzb+tdf

其中，tfy为拦截打击系统固有的反应时间;tzb为拦截打击系统固有的准备时间;tdf为导弹从发射到飞至杀伤近界的时间。

通过最小预警时间逆推所需的目标最小发现距离:

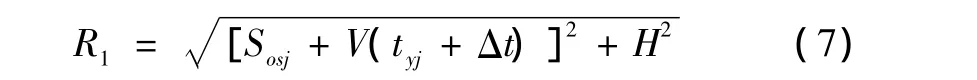
其中，H为飞机编队飞行高度，Sosj为目标高度H条件下拦截打击系统的水平杀伤近界。

2)保证尽远拦截的预警时间需求

预警时间:tyj=tfy+tzb+tdy

其中，tdy为导弹从发射到飞至杀伤远界的时间。

逆推所需发现目标距离:

其中，Sosy为目标高度H条件下拦截打击系统的水平杀伤远界。

3)判断预警时间是否满足拦截打击平台作战需求。

预警雷达发现目标的半径为R'。

① 如果R'＜R1，不具备拦截条件;

②如果R'＞R2，具备尽远拦截条件，飞机突防概率最小;

③ 如果R1＜R'＜R2具备拦截条件，但导致杀伤区压缩，压缩后的水平杀伤远界为:

其中，tys为导弹飞至杀伤区压缩后远界时间。

3.3 飞机编队突破防空体系的数学模型

1)防空体系未遭到破坏时，各个作战单元的能力属性配置往往能够保证Δt的取值满足R＞R2。此时体系满足最大拦截要求，预警指控系统能够充分支持拦截打击系统的要求。

式中，Dsy为火力单元的杀伤远界，Dsj为火力单元的杀伤近界，εmax为杀伤范围的最大张角。

2)随着体系遭到破坏，Δt可能增大，将出现R1＜R＜R2的情况，导致杀伤区被压缩。突防距离D为Δt的函数。

其中，S'sy为压缩后的水平杀伤远界。

3)当Δt继续增大到使得D=0的值时，飞机编队将顺利突防。

防空体系在被破坏的情况下，由于结构的不完整，体系中的火力节点的状态可能分布在能够最远拦截、能够压缩拦截、不能拦截三种状态中，此时飞机编队突防概率的表达式为:

4 算例分析

4.1 仿真计算

首先根据一般的装备能力水平设定计算飞机突防效果的参数值，如表2所示。

表2 各个参数设定值

由表2中数据计算可得:

由式(7)、式(8)可知，当感知节点到火力节点的时间t≤24s时，火力节点能够实现尽远拦截，24s＜t≤340s时，火力节点能够实现压缩打击，t＞340s时，火力节点无法打击目标。

为方便计算，假设t=2T，体系一刚好能发挥作用，反应时间为24s。

本文仿真使用的打击策略分为蓄意打击和随机打击两种。其中蓄意的打击顺序为:指控、传感器网络、火力节点，在打击过程中假设每类节点至少一个未被摧毁。图2和图3表示飞机编队突防概率随体系在两种打击策略下被破坏的变化。

图2 飞机突防概率随体系被蓄意破坏的变化

4.2 结果分析

从上面的仿真结果可以看出:

1)体系中少数节点具有很大的度，多数节点度很小，意味着体系的性能依赖少数节点，抗毁性差，在模型一、二、三中体现得比较明显。

2)网络的平均距离体现了网络的反应效率，反应越快的体系能应对越复杂的情况。具体到防空体系，反应迅速的防空体系可以抗击速度更快的飞机、充分地支持火力单元发挥作用。在蓄意打击仿真试验中，体系四、五在指控、传感器节点受到破坏时，火力单位数虽未减少，但体系反应时间增加，使得飞机编队的突防概率增大。

图3 飞机突防概率随体系被随机破坏的变化

3)聚类系数:该指标反映的是体系的集团化水平，集团内只要有一个节点与外界连接，外界的信息就能以最快的速度在集团内传递。对于防空体系，目标信息能够很快地传递到一个火力群中，减缓了因反应时间增长造成体系的防空能力的下降。模型四中，当体系遭到破坏，不是所有火力节点都直接与传感器节点相连时，飞机突防概率并未出现大幅度攀升，聚类效应在起作用。

4)模型四与前三个模型相比，在两个打击策略中都表现出了良好的抗毁能力和反飞机作战能力。仿真结果也说明了模型四与模型五的能力相差不大，但模型五中底层单元的完全互连增加了很大的开销，网络连通过于复杂。因此在防空体系构建时，在中间作战单元实现横向互连的基础上，底层作战单元无需完全互连，只需一定比例的横向互连即可。

5 结束语

防空体系反飞机的能力体现为飞机编队的突防概率，突防概率越低，体系的反飞机能力就越高。防空作战过程是一个对抗的过程，防空体系在对飞机编队作战之前往往受到一定程度的破坏。本文对具有不同网络特征的体系的反飞机能力随体系被破坏程度加深而变化进行了仿真分析，分析了度分布、平均路径长度、聚类系数这些网络特征参量对体系能力变化所起的作用，得出了以下结论。为提高防空体系对抗条件下的反飞机能力，需进行几个方面工作:1)防空体系在传统树状结构的基础上，指控单元需横向互连，底层作战单元与多个指控单元互连;2)底层作战单元进行一定比例的直接横向互连;3)防空体系具有聚类系数高、平均路径短、度分布较均匀的网络特征。该研究结果对防空体系的构建优化具有一定理论参考意义。

［1］Ganesh Bagler.Analysis of the Airport Network of India as a Complex Weighted Network［J］.Physica A，2008，387:2972-2980.

［2］Crucitti P，Latora V，Marchiori M.A Topologic Analysis of the Italian Electric Power Grid［J］.Physica A，2004，338:92-97.

［3］李德毅，王新政，胡钢锋.网络化战争与复杂网络［J］.中国军事科学，2006，19(3):111-119.

［4］吴柱侯，许腾.复杂网络理论军事领域运用研究现状［J］.国防科技，2010，31(5):1-6.

［5］Watts，D.J.，Strogatz，S.H.Collective Dynamics of Small·World Networks［J］.Nature，1998(393):440-42.

［6］Barabfisi，A.，Albert:Topology of Evolving Networks:Local Events and Universality［J］.Phys，Rev.Lett，2000(85):234-237.

［7］宋志华，张多林，朱法顺.一体化防空反导系统抗击能力建模与仿真研究［J］.军事运筹与系统工程，2009，23(2):61-66.