基于时滞的现代空防对抗兰彻斯特方程模型

2012-09-02胡浩然周存宝

指挥控制与仿真 2012年6期

文婧，胡浩然，周存宝

(1.陆军军官学院，安徽合肥 230031;2.解放军75569部队，海南海口 571146)

众所周知，现代局部战争大都从空袭开始。纵观近二十年来世界范围内所发生的几场局部战争(如海湾战争、阿富汗战争、科索沃战争、伊拉克战争、利比亚战争)，空袭与防空作战贯穿于战争的全过程。空袭与防空作战已成为现代战争的主要作战样式。同时，空防对抗也由过去的单一军(兵)种作战，或简单的多军(兵)种空中协同作战，发展为组织严密、结构配套、整体协同、体系对抗的联合作战样式。随着信息化武器装备和指挥信息系统建设的发展，人们在C4ISR系统的基础上融入杀伤(K)这一火力打击要素，导出了C4ISRK系统(指挥、控制、通信、计算机、情报、监视、侦察与杀伤)［3］。对空防对抗过程的研究成为一个较为困难、但又是必须致力解决的现实课题。本文尝试利用作战能力指数和时滞兰彻斯特方程相结合的方法，分析现代战争条件下的空防对抗过程。

1 基于时滞兰彻斯特方程的现代空防对抗模型

在现代空防对抗中，空袭一方为了达到减小突防损失的目的，常常采用大密度连续进袭的突防手段，使防空系统的拦截作战能力在某一特定时间内处于无法应付的境地，以达到提高突防概率的目的。在现代空袭条件下，如何对防空武器系统的防空作战过程做出比较精确的描述，建立地空导弹武器系统的防空对抗模型是十分必要的，它不仅可为防空力量部署的拦截作战能力做出评价，而且可以掌握在防空战斗进行的某一时刻双方兵力的期望数量，从而也可为防空力量部署提供一定的参考。

现代空防对抗中进攻方的运用特点，有了比以往更多的攻击方式，主要具有4个特点:1)兵力集中，隐蔽突然，全方位连续进袭，扩大攻击正面;2)多机协同，小编队、多层次、一体化综合突击，提高攻击效率;3)主、佯攻结合，分散火力;4)多重突防手段综合使用，以增大突防概率。防御方也有了新的特点，在进攻方飞机群入侵和地空导弹、高炮火力网等武器系统拦截作战过程中，地空导弹武器系统一般是在本方领土上进行作战，武器系统有时间、有条件进行伪装隐避或设置假目标，进攻方飞机很难准确判断地空导弹武器系统所处的位置［6］。为了建立现代信息化条件下空防对抗模型，先作如下四点假设:

1)进攻方飞机入侵服从强度为λ的泊松流;

2)进攻方飞机对地攻击武器分为精确制导武器和一般武器，且所有来袭飞机挂载弹量相同，弹种相同;

3)防空武器系统中的高炮火力单元在被摧毁前，具有平均发射流;

4)防空武器分主要有地空导弹和高炮。

一般情况下，进攻方飞机精确制导武器的攻击服从兰彻斯特方程平方律，而一般性攻击武器则服从兰彻斯特方程线性律。同理防御方地空导弹对进攻方飞机攻击满足兰彻斯特方程平方律，而高炮等一般性防空武器则满足兰彻斯特方程线性律。则在上述假设条件下，可以建立如下基于时滞的空防对抗兰彻斯特方程模型:

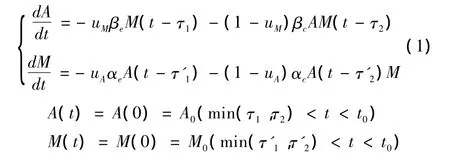
式中，A(t)表示进攻方来袭飞机数量，M(t)为防御方防空火力单元数;uM为防空火力单元中精确制导武器(地空导弹)所占比重，uA为来袭飞机所中所载精确制导武器(空地导弹)比重;βe为防空导弹平均毁伤系数，βc为防空高炮平均毁伤系数;αe为来袭飞机精确制导武器平均毁伤系数，αc为来袭飞机一般武器平均毁伤系数。

2 空防对抗模型参数求取

由假设可知，进攻方飞机按泊松分布随机到达，即在时间间隔t内，飞机来袭数量为k架的概率由式(2)给出:

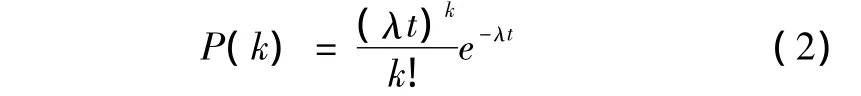
假设在某一时刻，防空系统的各个火力单位都可以对进攻方的作战单元进行搜索。不论进攻方飞机是否开火，防御方火力单元对一个指定的进攻方飞机的平均搜索发现概率为λ1(t)，搜索发现时间服从参数为λ1(t)的指数分布，且各个火力单元的搜索时间相互独立。由以上分析可得，若以q(t)为［0，t］时间内防御方单个火力单元发现进攻方飞机的概率，则

则防御方火力单元未发现一架飞机的概率为

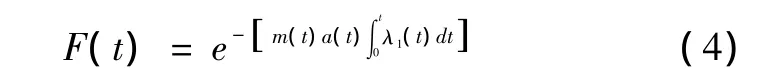
防御方火力单元至少发现一个目标的概率为

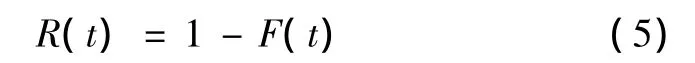
由于进攻方飞机入侵流服从平均强度为λ的泊松流，当空袭形成长时间连续攻击，且拦截纵深不大时，可将防空系统看作是消失制的随机服务系统，利用随机服务系统理论中的“埃尔朗”公式去估算每个空中目标受到射击的概率［6］

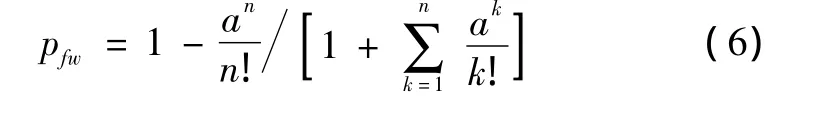
式中，n为目标通道数，这些目标通道必须能在拦截区范围内全方位调度;α为综合参数，它是平均射击时间与平均等待时间(目标在发射区的停留时间)的比值。

对来袭飞机而言，在防空导弹(以俄罗斯S300为例)单发命中条件下即意味着摧毁即毁伤概率为1，而高炮(以某高炮为例)单发命中条件下却不一定就摧毁。假设对高炮而言单发命中概率为PH，k发命中条件下毁伤概率为P1kS，由建模假设(3)可令，高炮战斗平均射速为ts，每次射击弹数为λ2发，则

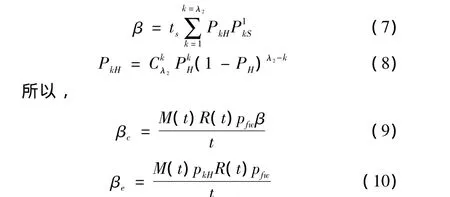
同理，如果来袭飞机都可以对防御方的防空作战单元进行搜索，且其平均搜索发现概率为λ2(t)，各个飞机的搜索时间相互独立，则来袭飞机至少发现一个防空火力单元的概率为

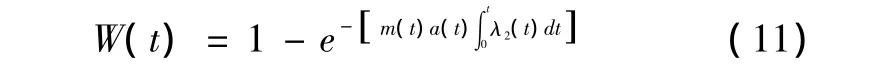
对防空武器而言，只要被空地导弹(以某空地导弹为例)命中就意味着基本丧失战斗力，即可以认为单发命中条件下的毁伤概率为1;另假设在一般性空中武器(主要为普通炸弹)单发打击命中毁伤概率为PA，k发命中条件下毁伤概率为P2kS，假设飞机每次投弹速度为t2，每次射击弹数为λ3发，则

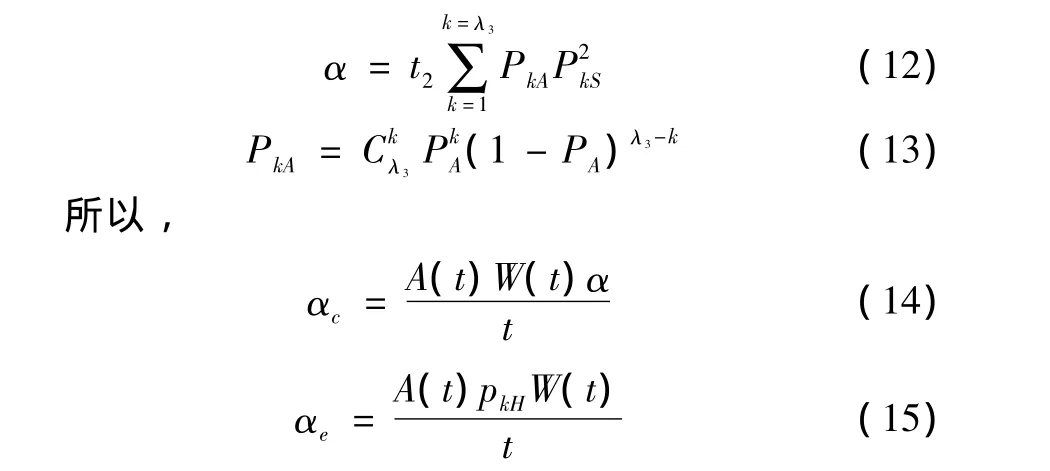
将式(9)，(10)，(14)，(15)代入式(1)可得空防对抗体系作战模型为

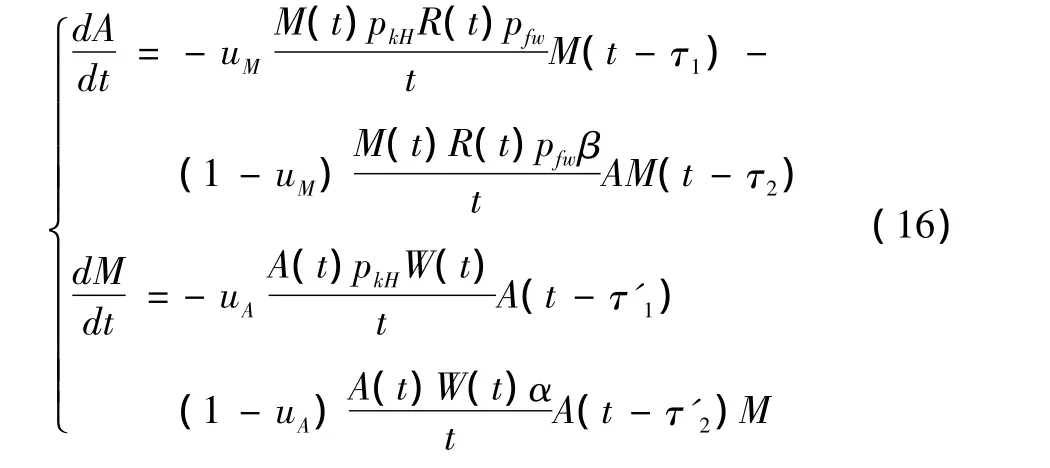
式中，时滞量因信息化程度及各作战单元反应时间和武器信息化程度不同而不同。

对于所建立的空防对抗兰彻斯特方程模型，可借助于Matlab-Simulink工具箱进行仿真计算，其计算过程可采用基于隐式的Runge-Kutta法。其仿真模式如图1所示。

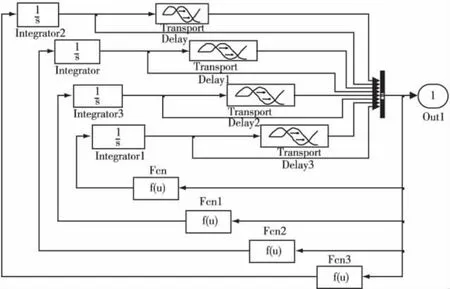
图1 仿真模型图

3 算例仿真与结果分析

假设红蓝双方空袭兵力与防空兵力及平均毁伤系数相等，但信息化程度不对称。取A(0)=x(0)=10000，M(0)=y(0)=10000;αe= βe=0.1，αc= βc=0.00001;uM=0.1，uA=0.2。当τ1=0，τ2=0，τ'1=0，τ'2=0时，即时滞量为零时的仿真计算结果如图2所示。当 τ1=0.5，τ2=0.5，τ'1=0，τ'2=0 时的仿真计算结果如图3所示。

图2 仿真结果1

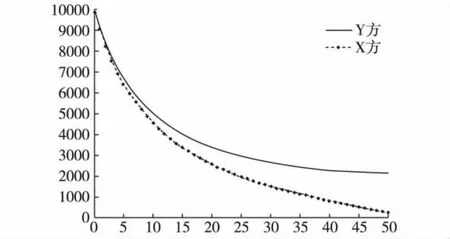
图3 仿真结果2

比较分析图2与图3可以看出，由于时滞量影响了战斗损耗速率。在实际作战中，反应滞后将带来更大程度的伤亡和更快的战斗减员。

当 A(0)=x(0)=11000，M(0)=y(0)=10000，τ1=0，τ2=0，τ'1=0，τ'2=0 时的仿真计算结果如图4 所示;当 τ1=0.5，τ2=0.5，τ'1=0，τ'2=0 时的仿真计算结果如图5所示;当τ1=0.8，τ2=0.8，τ'1=0，τ'2=0时的仿真计算结果如图6所示。

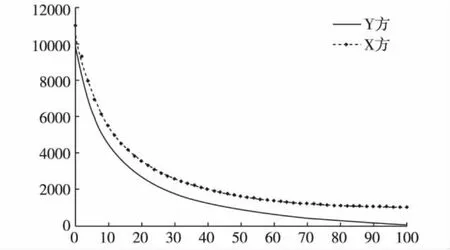
图4 仿真结果3

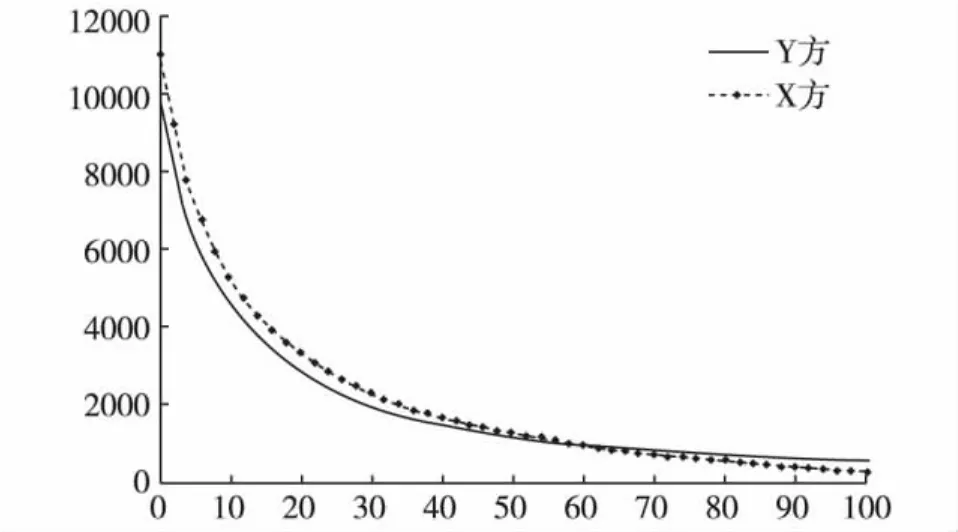
图5 仿真结果4

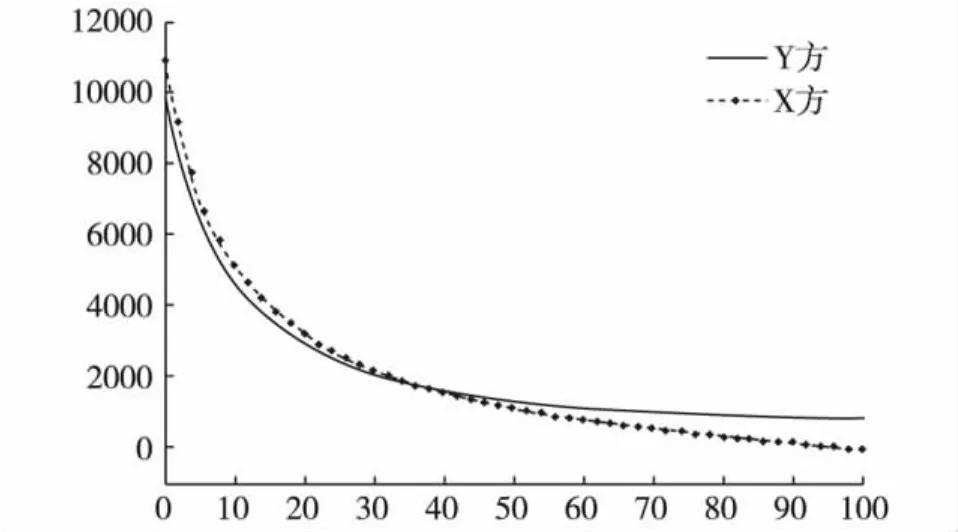
图6 仿真结果5

分析图4、图5、图6可以看出，时滞量可能会引起整个战斗结局的转变，而且时滞量越大，战斗结局转变越快。在实际作战过程中，即便在初始战斗力小于对手的情况下，迅速的情报获取与处理能够掌握战斗的主动，给对手以更加致命的打击。从图5与图6的比较分析中可以看出，能获得先于对手更多的信息处理时间(有限时滞量)，则其信息优势越明显。