V掺杂ZnO性质的第一性原理研究

王丽丽，季燕菊，付刚

(山东建筑大学理学院，山东 济南 250101)

0 引言

近些年来，纤锌矿ZnO的Ⅱ－Ⅵ族直接带隙宽禁带氧化物半导体材料成为研究的热点。它具有大光电耦合系数、低介电常数、高化学稳定性、高的激子结合能(60mev)及优良的光电、压电特性，它在室温下的禁带宽度为3.2eV[1]，在透明导电薄膜、光电器件等领域有广泛的应用[2－4]。在 ZnO中掺杂不同的元素，能改变ZnO的结构和带隙宽度，使掺杂ZnO具有新的特性。理论计算表明[5]，ZnO掺杂V、Cr、Co等元素能够产生自旋极化，形成高于室温的稀磁性透明半导体[6]，是下一代微电子和光电子领域自旋电子学器件有重要价值的材料之一。根据理论计算，V掺杂的ZnO膜具有最高的居里温度。Saeki等[7]利用激光脉冲法制备出居里温度高于350K的钒掺杂铁磁性氧化锌膜。Vyatkin实验小组[8]用钒离子注入法获得氧化锌磁性膜。目前借助第一性原理研究V掺杂ZnO的电子结构及相关性质的报道较少，本文利用第一性原理方法对VxZn1－xO(X=0，0.042，0.083，0.125)的结构进行了研究，这种方法的可靠性已经得到大量实际计算的验证[9，10]。

1 模型构建与计算方法

本文采用基于密度泛函理论(DFT)和平面波赝势技术的CASTEP软件包对纤锌矿VxZn1－xO的能带结构和态密度进行了计算，为尽量减少平面波基矢个数，采用了超软赝势来描述离子实与价电子之间的相互作用，选取 O-2s22p4，Zn-3d104s2，V-3d34s2组态电子作为价电子，其余轨道电子视为芯电子进行计算。

理想的 ZnO是六方纤锌矿结构，对称性为C6v－4，属于 P63mc空间群，每个原胞有 4个原子，晶格常数为 a=b=0.3249nm，c=0.5206nm，α =β=90°，γ =120°，其中 c/a 为1.602。

本文计算中使用的超晶胞模型分别为ZnO(2×2×2)超晶胞，1个V原子替代1个Zn原子的ZnO(2×3×2)超晶胞、2个V原子替代2个Zn原子的ZnO(2×3×2)超晶胞和2个V原子替代2个Zn原子的ZnO(2×2×2)超晶胞使得V的掺杂浓度分别为 0、4.2%、8.3%、12.5%。为了保证计算精度，平面波截止能设为340eV，对布里渊区的积分计算使用 Monkors－Pack[11]方案，k点选取分别为 4 ×4 ×2，4×3×2，4×3×2和4×4×2，自洽收敛标准设为每个原子 2×10－5eV，每个原子上的力不大于0.5eV/nm，晶体内应力不大于0.1Gpa。

2 结果与讨论

2.1 结构优化

图1所示，是VxZn1－xO优化后得到的折合晶胞常数随掺杂量X的变化，随掺杂量X的增大，掺杂后的晶格常数a和c呈线性的增大，晶格发生了微小膨胀，与实验[12]中得到的结构吻合，引起这种变化的主要原因我们认为是由于V离子半径与Zn离子半径不同，V离子对Zn离子的代替引起晶格尺寸失配，产生了应变，从而导致晶格略微变大，而在Sn掺杂In2O3材料中这种现象也被发现过。

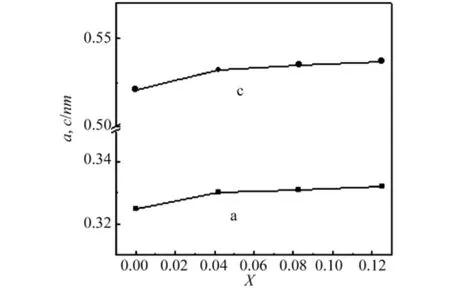
图1 VxZn1－xO的折合晶胞常数随掺杂量X的变化

2.2 能带结构与态密度

2.2.1 ZnO的能带结构和态密度

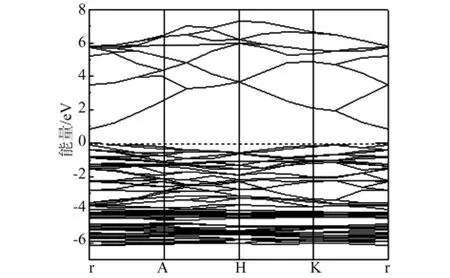
图2 纤锌矿ZnO的能带结构

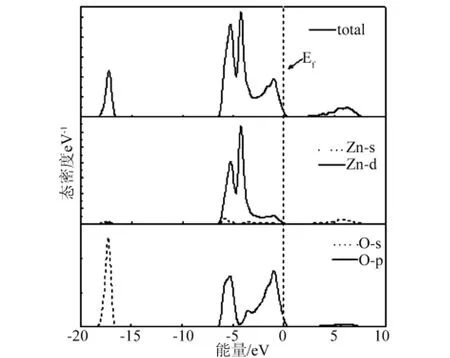
图3 纤锌矿ZnO总态密度和分态密度

本文中，对ZnO优化后，计算了ZnO的能带结构、总态密度和分波态密度，如图2、3所示，计算出带隙值为0.809eV，与其他文献带隙值(文献[13]为0.80eV，文献[14]为 0.73eV)基本一致，费米能级(Ef)设置为0，ZnO的价带顶和导带底同位于布里渊区的高对称点Γ点，是典型的直接带隙半导体的能带结构，在－18.3eV～－16.5eV存在定域性很强的O-2s电子，在－6.5eV～0eV之间主要是Zn-3d态电子和O-2p态电子构成，价带顶由O-2p态电子控制，导带底由Zn-4s态电子控制，导带由O-2p和Zn-4s态电子构成，但Zn-4s态电子是主要贡献，且电子具有从Zn-4s态到O-2p态的跃迁现象。

2.2.2 V0.125Zn0.875O 的能带结构和态密度

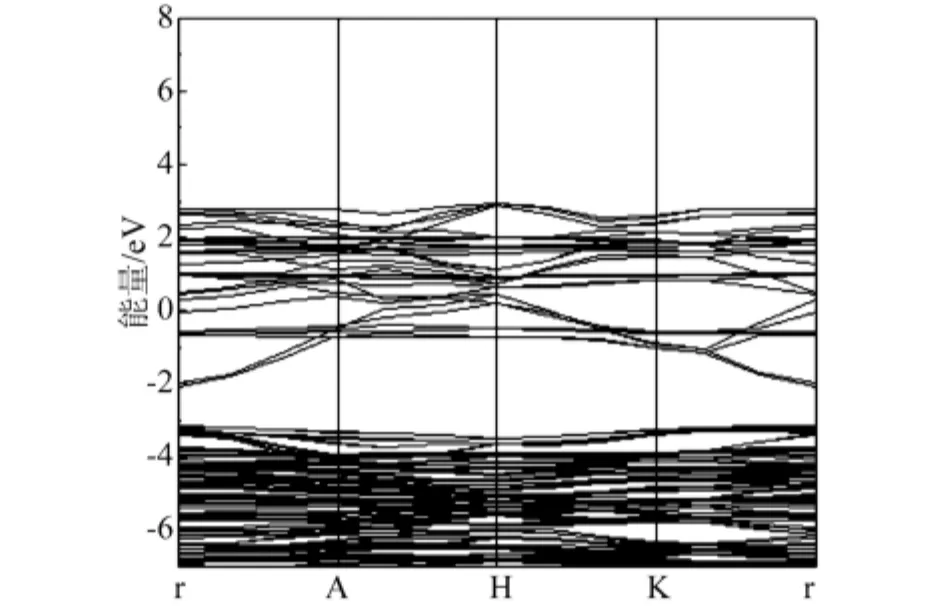
图4 V0.125Zn0.875O 的能带结构

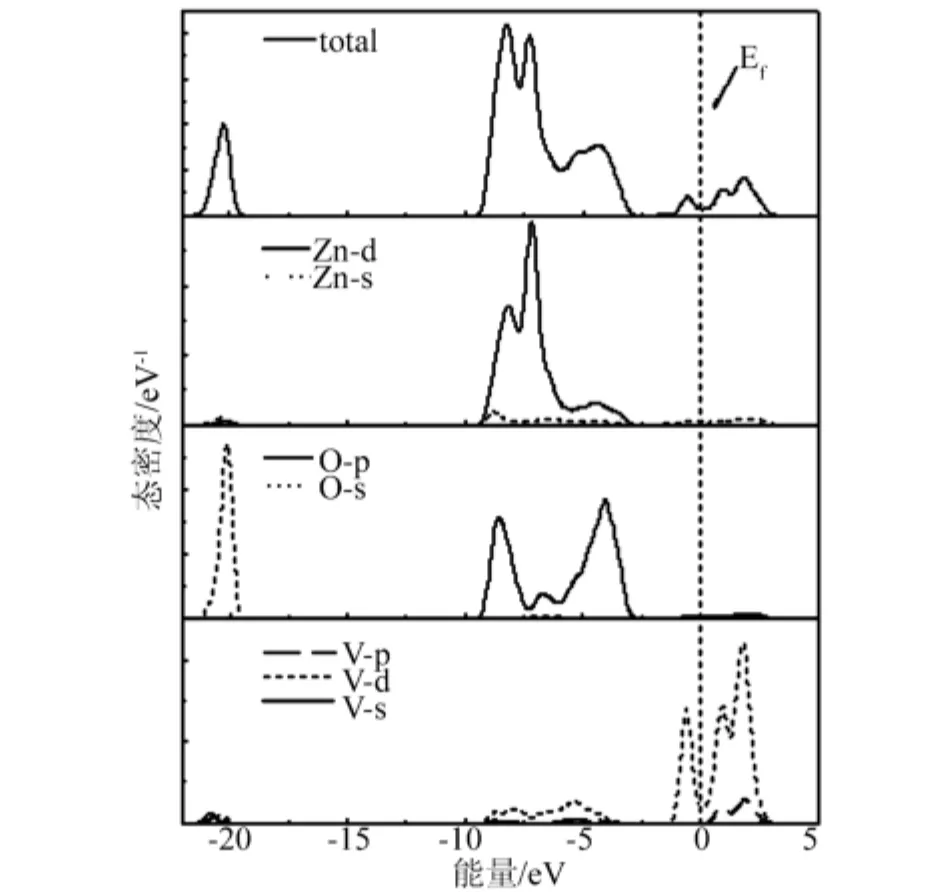
图5 V0.125Zn0.875O 的总态密度和分态密度

图4、5 给出了 V0.125Zn0.875O 的能带结构和态密度，由图4与图2比较可知，V掺杂ZnO之后，禁带宽度变小，体系引入的杂质能级靠近导带底，费米能级进入了导带并且穿插在杂质能级中，相对于ZnO来说，掺入V之后相当于一个半导体的n型掺杂。同ZnO的态密度相比，V掺杂后，－21.4eV～－19.4eV主要由O-2s态电子贡献，－9.5eV ～ －2.7eV范围内的态密度主要由O-2p态电子和Zn-3d态电子构成，在－1.4eV ～3.2eV 范围内，V-3d电子态远大于最邻近的O原子和次邻近的Zn原子，是主要组成部分，有较强的局域性。价带顶仍由O-2p态电子控制，导带底由V-3d态电子控制，导带由Zn-4s，O-2p和V-3d3p态电子共同构成，杂质能级主要来源于V-3d态电子。

2.3 V掺杂ZnO的磁性

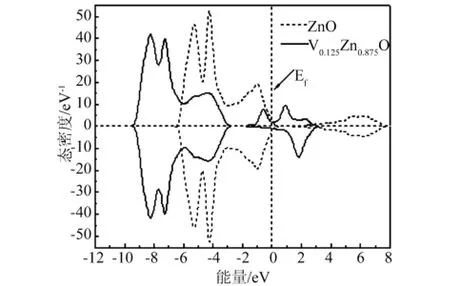
图6 纯 ZnO和V0.125Zn0.875O的自旋态密度

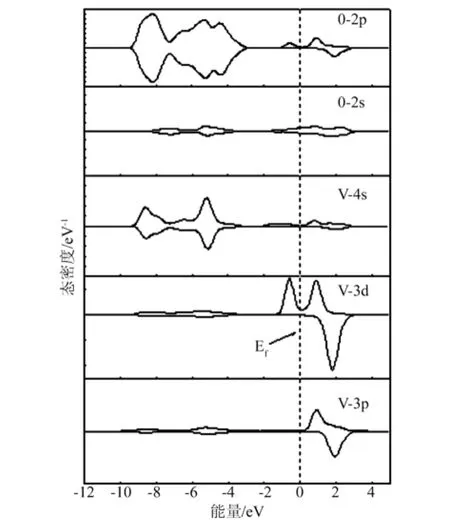
图7 V0.125Zn0.875O 的自旋分波态密度

从图6中可以看出，V掺杂ZnO的自旋态密度在费米能级附近，自旋向上和自旋向下的电子态密度分布具有不对称性，自旋向上和自旋向下的电子都发生了移动，而且自旋向上的电子数比自旋向下的电子数多，对态密度进行积分后发现V掺杂ZnO体系表现出净磁矩，具有磁性，因为在2eV附近的态密度峰对应空能级，因此磁性主要来源于－2eV～1eV附近的那两个态密度峰，而这两个峰主要由V-3d3p态电子与O-2p态电子组成。结合图7发现，当V掺杂后，V-3d态电子与O-2p态电子的态密度分布大部分重合，形成了pd杂化，这为稀磁半导体材料具有新颖的磁光和磁电性能提供了依据[15]。

3 结论

本文采用了DFT结合超软赝势的方法，对掺杂V的ZnO性质进行了研究，通过对掺杂前后ZnO的能带结构、态密度等的比较，发现V掺杂ZnO后，随着掺杂量X的增大，晶格发生了微小膨胀，这对带隙减小有一定的作用。V的掺杂属于ZnO的n型掺杂，在费米能级附近，态密度分布具有不对称性，表现出了磁性，而磁性主要来源于V-3d3p态电子与O-2p态电子组成的那两个态密度峰。V-3d态电子与O-2p态电子形成了pd杂化，这对掺杂后的材料具有磁光和磁电性能提供了依据。

[1]Fan X.M.，Lian J.S.，Guo Z.X.，et al.Microstructure and photoluminescence properties of ZnO thin films grown by PLD on Si(111)substrates[J].Appl Surf Sci，2005 ，239(2):176 －177.

[2]霍庆松，张宁玉，付刚，等.衬底及压强对磁控溅射ZnO薄膜表面形貌的影响[J].山东建筑大学学报，2010，25(4):382－384.

[3]韩利新，张宁玉，霍庆松，等.Er/Yb/Al掺杂ZnO薄膜的结构与形貌研究[J].山东建筑大学学报，2011，26(5):425－428.

[4]Aoli T.，Hatanka Y.and Look D.C.，ZnO diode fabricated by excimer-laser doping[J].Appl Phys Lett，2000，76(22):32 －38.

[5]Wang Q.，Sun Q.，Chen G.，et al.Vacancy-induced magnetism in ZnO thin films and nanowires[J].Phys Rev B，2008，77(20):5411.

[6]肖振林，史力斌，利用第一性原理研究Ni掺杂ZnO铁磁性起源[J].物理学报，2011，60(2):027502.

[7]Saeki H.，Tabata H.and Kawai T.，Magnetic and electric properties of vanadium doped ZnO films[J]. Solid State Communications，2001，120:439 －443.

[8]Vyatkin A.F.，Zinkenko V.I.，Agaphonov Y.A.，et al.Nuclear instruments and methods in physics research section B[M].Beam Interations with Materials and Atoms，2005，237(1):179－182.

[9]喻力，郑广，何开华，等.过渡金属掺杂SnO2的电子结构与磁性[J].物理化学学报，2010，26(3):763－768.

[10]陈琨，范广涵，章勇，等.N掺杂p－型ZnO的第一性原理计算[J].物理化学学报，2008，24(1):61－66.

[11]Pack J.D.and Monkhorst H.J.，“Special points for Brillouinzone integrations”-a reply[J].Phys Rev B，1977，16(4):1748－1749.

[12]阮宜斌，孟立建，梁二军.V含量对ZnO薄膜结构及光学特性的影响[J].无机化学学报，2006，12:2248.

[13]Janotti A.，Segev D.and Van De Walle C.G.，Effects of cation d states on the structural and electronic properties ofⅢ-nitride andⅡ-oxide wide-band-gap semiconductors[J].Phys Rev B，2006，74(4):045202.

[14]刘小村，季燕菊，赵俊卿，等.In掺杂ZnO电子结构的第一性原理研究[J].物理学报，2010，59(7):4925.

[15]刘学超，陈之战，施尔畏，等.ZnO基稀磁半导体磁性机理研究进展[J].无机材料学报，2009，24(1):3－6.