DDA用于重力坝深层抗滑稳定的接触刚度取值

2012-08-29尹晓楠张国新

中国水利水电科学研究院学报 2012年4期

尹晓楠，张国新

（中国水利水电科学研究院结构材料研究所，北京 100038）

1 研究背景

重力坝安全的核心是抗滑稳定，包括沿建基面的抗滑稳定和深层抗滑稳定。据不完全统计，我国已建、在建重力坝中，有30%存在深层抗滑稳定问题，需要核算深层抗滑稳定[1-2]。深层抗滑稳定的计算一般采用刚体极限平衡法[3]，有时采用有限元等数值方法。刚体极限平衡法概念清晰、简单、实用，但只适用于双滑面且滑面折点位于坝址下游的情形。为此陈祖煜[3]提出将边坡稳定分析的SARMA法应用于重力坝深层抗滑稳定，但是SARMA法与常规的刚体极限平衡法相同，都要假定块体之间的传力角，计算出的安全系数受传力角的影响较大，同时全滑面达到极限状态相当于假定沿滑裂面的屈服满足理想弹塑性准则，这与岩石类材料的破坏模式不符，且SARMA法不能给出沿程点安全系数的分布，因此在应用上设置了一个较大的安全系数。

数值方法以有限元为主[4]，分为线弹性和非线性。线弹性有限元计算时需要应力插值、积分，可能会带来较大误差。为了克服这个不足，张国新在文献[5]中提出了直接反力法，该方法可以较高精度的求出滑裂面力的分布，避免了应力插值、积分等带来的误差。但线弹性方法都存在一个问题，即只能求给定滑动面的安全系数，最小安全系数滑裂面需要进行大量试算求出。非线性有限元分析可分为超载法和强度折减法，非线性方法可以模拟渐进破坏过程，自动搜索滑动面，但存在计算结果受网格剖分影响较大，在滑动面形成时会出现大面积屈服，安全系数难以准确确定等不足。

石根华提出的非连续变形分析（DDA）[6]是以块体为基本单元，块体之间的接触面可以构成潜在的滑动面，计算得到的接触力可以有很高的精度。张国新、金峰曾在文献[7]中介绍过DDA和有限元用于深层抗滑稳定的比较，表明DDA用以分析重力坝深层抗滑稳定具有一定的精度优势，但与其它块体类方法类似，接触力的分布往往与接触刚度取值有关，这会影响到局部甚至整体安全系数的计算结果。本文以武都RCC重力坝的坝基及深层抗滑稳定为例研究DDA用于重力坝抗滑稳定分析的接触刚度取值。

2 基于DDA的重力坝抗滑稳定计算方法

2.1 滑动面接触力计算石根华提出的DDA[6]，将构造面相互切割成的不规则块体作为基本单元，以块体的刚体位移和应变为基本未知量，见图1。块体之间用接触弹簧相互连接，通过最小势能原理求出块体系统的瞬时弹性方程，求解方程后可以求出各时刻的块体位移和变形，进而求出块体之间的接触力。

块体的位移可用下式表示：

式中：x0、y0为块体形心坐标；u0、v0、r0为形心在x、y方向的位移及转动角；εx、εy、γxy为x、y方向的正应变和剪应变。

考虑块体的弹性势能，各种荷载的作用功，块体之间的接触弹性势能采用最小势能原理可以求出，DDA瞬时弹性方程为：

求解方程（2）可得到各块体的形心位移及应变，再用式（1）表示各种块体的变形函数。

接触应力可用下式计算：

式中：Pn、Pt为法向及切向弹簧刚度；dni、dti为第i接触点的法向及切向接触变形，详见文献[6]；li为第i点控制的接触长度。

2.2 局部及整体安全系数

式中：ci、fi为第i段接触面的黏聚力及摩擦系数。

3 计算模型及参数

本文以武都碾压混凝土（RCC）重力坝的18#坝段为例研究DDA用于重力坝抗滑稳定分析的适应性及刚度参数取值。该工程位于中国四川省绵阳市，最大坝高120m，坝顶长727m，库容5.72亿m3。大坝坝基内贯通的缓倾裂隙、断层及层间错动带形成天然滑移面，大坝沿建基面及沿深层软弱夹层结构面的抗滑稳定性是建设中需解决的关键问题。

18#坝段坝体及基础构造见图2，根据四川省水利水电勘测设计研究院《四川武都引水第二期工程武都水库技施设计阶段大坝深层抗滑稳定设计报告》滑面组合断层10F2+F115组合面是18#坝段的最不利的组合面。因此，本次计算以该滑面组合为计算对象，材料力学参数见表1，裂隙力学参数见表2。

表1 DDA计算用的材料力学参数

表2 各类结构面力学参数

4 沿建基面抗滑稳定

4.1 刚体极限平衡法计算结果刚体极限平衡法沿建基面安全系数按下式计算：

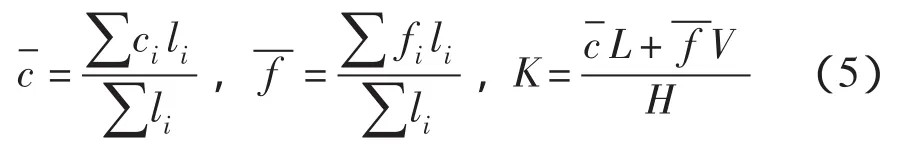
采用表3的参数计算武都大坝坝体在正常水压力作用下沿建基面的抗滑安全系数为3.5，其中垂直力V=15835t/m，水平力H=5322.2t/m。

表3 武都建基面材料参数

4.2 建基面整体抗滑稳定安全系数的DDA分析

采用图3所示的两种方式，用DDA计算沿建基面的整体安全系数。计算取不同的接触刚度，法向刚度从0.001Er～1000Er。Er为基础岩石弹模，剪切刚度为法向刚度的0.4倍。

计算结果表明：用图3所示的两种DDA模型计算得到整体安全系数均为3.51（见图4），且与接触刚度无关（见图4），同时法向合力与切向合力与理论值一致，说明DDA用于计算单滑面的整体抗滑稳定时可以得到不受参数和模型影响的精确解。

图4 不同接触刚度安全系数随计算结果

4.3 建基面局部抗滑稳定安全系数的DDA分析沿滑裂面的局部安全系数取决于正应力和剪应力的沿程分布。图5（a），（b）表明，沿建基面的法向应力分布与接触刚度取值无关，但剪应力分布与接触刚度取值关系密切。接触刚度越小剪应力沿程分布越均匀，最大剪应力越小；接触刚度越大，剪应力沿程分布变化越大，最大剪应力也相应越大，最大剪应力出现在坝踵处。当剪切刚度达到10Er以上时，剪应力趋于稳定。图5（c）为接触面局部安全系数分布随接触刚度的变化，剪应力越大安全系数越小，故最小安全系数也出现在坝踵处，接触刚度越大，最小安全系数越小。

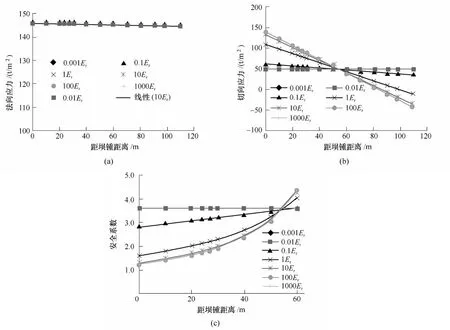
图5 局部安全系数沿程分布

5 深层抗滑稳定的DDA分析

5.1 深层抗滑稳定整体安全系数的DDA分析图6所示沿10F2—F115滑动面的安全系数计算模型简化为以下4种形式。第1种形式为基础内部取10F2—F115滑动面，与建基面一起将坝体及基础切割成3个DDA单元。第2个模型采用与Sarma法相同的模型即在滑动面折点出设一切割面，与滑动面、建基面一起将坝体和基础切割成8个DDA单元。第3个模型采用基础内实际构造面将坝体和基础切割成59个DDA单元。第4个模型将10F2—F115滑动面上的DDA基础剖分为许多条形块体，形成43个DDA单元。

4种模型取不同接触刚度的计算结果见图7。

图7 4种模型的计算结果

计算结果表明：单滑块模型Ⅰ受接触刚度的影响较大，随着接触刚度的增加，单滑块模型安全系数由2.0逐步增大到5.0，当接触刚度大于基础弹模后，安全系数稳定在5.0；Sarma模型计算得到的安全系数受接触刚度影响较小，在接触刚度大于基础弹模后安全系数稳定在1.35附近；实际构造模型的安全系数在接触刚度小于基础弹模时，随接触刚度增大而逐步增大，当接触刚度大于基础弹模后，安全系数稳定在1.76附近；单滑块模型Ⅱ的安全系数随接触刚度增大只有略微的增大，由1.80增加到1.87，表明单滑块模型Ⅱ安全系数受接触刚度影响较小。

5.2 接触刚度对应力分布的影响为分析接触刚度对安全系数的影响，按照图8所示，给出单滑块模型Ⅰ和实际构造模型第一滑面和第二滑面上剪应力及压应力随接触刚度的变化图。

表4 深层抗滑稳定的Sarma法和DDA法计算结果对比

图9表明，两种模型的第一滑面法向力N1均随接触刚度的增大而减小，第二滑面法向力N2随接触刚度的增大而增大，说明接触刚度会影响作用力在两个滑面上的分布。分析单滑块模型Ⅰ安全系数偏大的原因，随接触刚度的增大，第一滑面A点的压力由压变为拉，并且逐步增大，当A点的拉应力达到给定的抗拉强度时A点张开，将AB段承担的法向及切向力转移至BC段。对于单滑块模型，由于A点代表的接触段长度为AB的一半，所以A点一旦张开，AB段的一半即张开，失去承载力后A点承担的荷载大部分转化为BC段的法向力N2，所以单滑块模型Ⅰ的安全系数会随接触刚度增大而偏大。

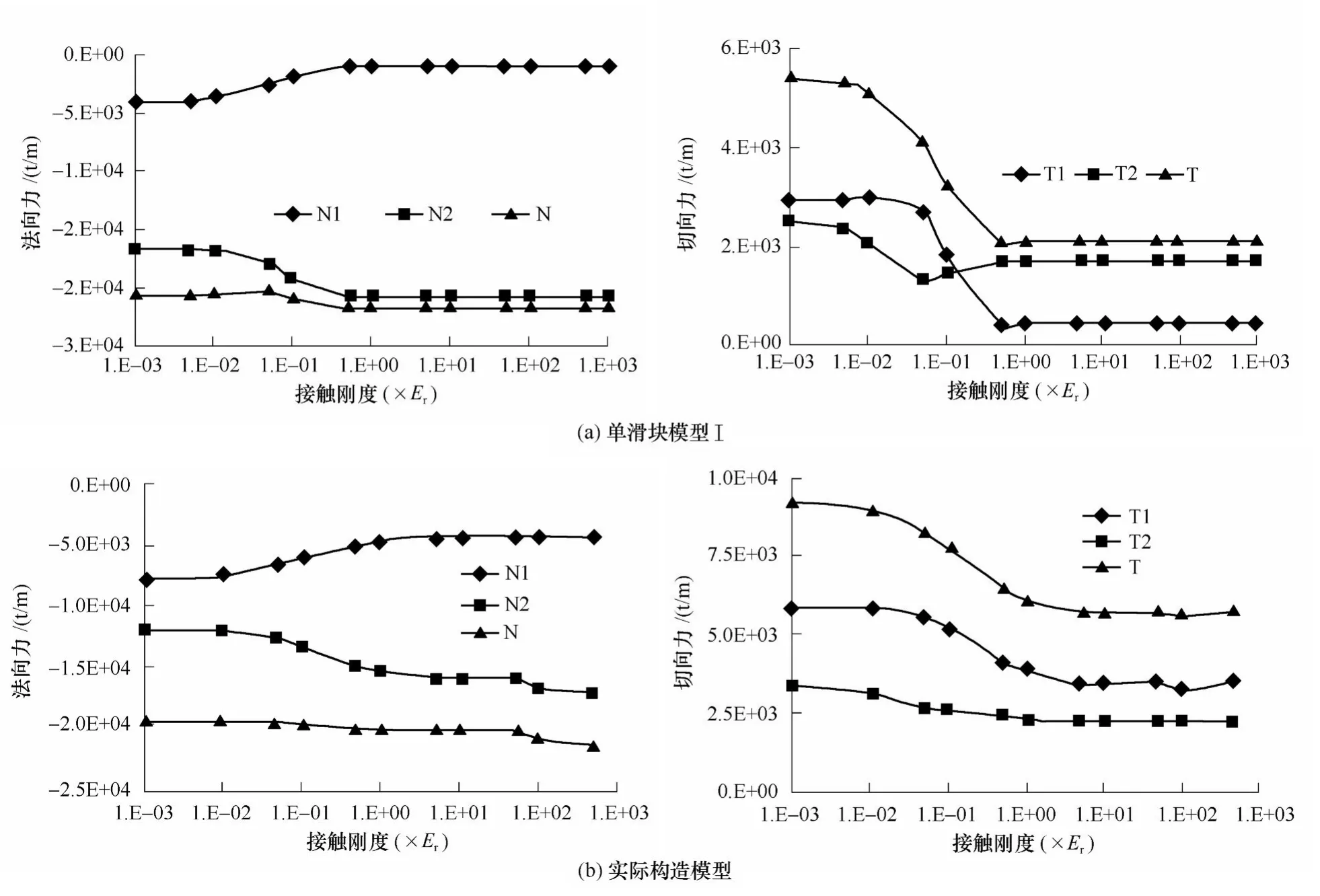
图9 两种模型两个滑面上法向和切向力随接触刚度的变化

理论分析表明，当AB段完全脱开，全部荷载由BC段承担时，其安全系数为8.02且不随接触刚度的变化而变化。而实际模型由于沿滑动面分段数目较多，A点张开后只有局部的一小部分失去承载力，故反力N1、T1向BC段转化的较小，所以对安全系数的影响较小。为了验证此分析，可将单滑块模型细分为很多小块（单滑块模型Ⅱ），计算该模型得到的安全系数几乎不受接触刚度的影响。

5.3 与sarma法的比较图6中模型2为Sarma法计算模型，利用该模型取不同的侧面摩擦角可得到不同的安全系数见表4，表中同时给出了接触刚度取10Er时DDA的计算结果。

表4可知，当侧面摩擦角取值较小时，Sarma法和DDA法计算的结果非常相近，而随着摩擦角取值的增大，两者计算的安全系数都不断变大。DDA的计算结果随摩擦角的增大而逐步与单滑块模型Ⅰ接近。