剖析直线与方程的七大易错点

☉浙江省宁波市北仑职业高级中学 任海娜

直线与方程是高考内容的重要组成部分，我们必须熟练掌握直线的倾斜角和斜率、直线方程的几种形式，避免错误的发生，准确、迅速地解决问题.本节常见的思维误区有：

（1）在对直线的倾斜角和斜率的学习中，未能充分理解倾斜角和斜率之间的区别与联系.

（2）在本章的学习中，要强化数形结合和分类讨论的思想方法，极易忽略考虑斜率是否存在？

一、对直线的倾斜角与斜率的概念理解不透彻

例1 下列说法中正确的有（ ）.

①若直线的倾斜角为θ，则直线的斜率为tanθ；

②因为所有的直线都有倾斜角，所以所有的直线都有斜率；

③因为垂直于x轴的斜率不存在，所以垂直于x轴的直线的倾斜角也不存在.

A.0个 B.1个 C.2个 D.3个

错解：选D.

错解分析：本题考查斜率与倾斜角的关系，所有直线都有唯一的倾斜角，但当倾斜角为90°时，直线的斜率不存在，所以三句话都错.

正解：选A.

二、误解斜率与倾斜角的对应关系

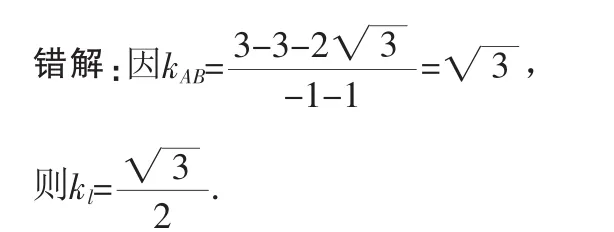
错解分析：产生错误的原因在于对斜率与倾斜角的对应关系一知半解，误认为倾斜角的倍数关系等同于斜率的倍数关系.解决此题的关键是求出直线AB的倾斜角为60°，则直线l的倾斜角为30°，由此可得直线l的斜率.

则直线AB的倾斜角为60°.

由题意可知直线l的倾斜角为30°.

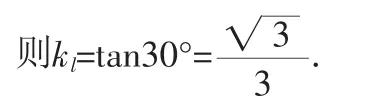
三、由于正切函数单调性理解不透彻，造成斜率的单调性掌握不准确

例3 已知点A（-3，4），B（3，2），过点P（2，-1）的直线l与线段AB有公共点，求直线l的斜率k的取值范围.

错解：由已知得：

则直线l的斜率k的取值范围是-1≤k≤3.

则要使直线l与线段AB有公共点，直线l的斜率k的取值范围是k≤-1或k≥3.

四、误把k1=k2看成是直线l1∥直线l2的充要条件

例4 根据下列给定的条件，判断直线l1与直线l2是否平行.

（1）直线l1过点A（2，1），B（2，5），直线l2：x=-4.

（2）直线l1过点A（0，1），B（-2，-1），直线l2过点C（3，4），D（2，3）.

错解分析：两题都误把k1=k2看成是直线l1∥直线l2的充要条件，忽略了限制条件.判断两直线是否平行时，一个要注意斜率是否存在，如（1），虽然斜率不存在但并非倾斜角不存在，不重合的两条直线，如果斜率不存在，那么这两条直线显然平行；另一个要注意两条直线是否重合，如（2），虽然也满足k1=k2，但由于在一条直线上，所以l1与l2重合.

五、易忽略直线斜率不存在的情况

例5 设直线l的方程为（m2-2m-3）x+（2m2+m-1）y=2m-6，若此直线的斜率为1，试确定实数m的值.

错解分析：当2m2+m-1=0时，直线的斜率不存在，错解忽略了这一点.

六、误把截距等同于距离

例6 求过点A（-4，1），且在坐标轴上截距相等的直线l的方程.

错解：由题意得直线l的倾斜角α=45°.

则k=1，又过点（-4，1），

则直线l的方程为x-y+5=0.

错解分析：此解其中一个错误就是误把截距等同于距离，另一个错误是忽略了一种特殊情况——过原点的直线，它也符合在坐标轴上截距相等的条件.

正解：由题意得直线l的倾斜角为135°或过原点.

当α=135°时，k=-1，又因为过点（-4，1），所以直线l的方程为x+y+3=0；

当直线过（-4，1），（0，0）时，直线l的方程为x+4y=0.

综上所述，所求直线方程为x+y+3=0或x+4y=0.

七、直线方程的几种形式及其适用范围掌握不熟练而出错

例7 当a为何值时，直线l1：（a+2）x+（1-a）y-1=0与直线l2：（a-1）x+（2a+3）y+2=0互相垂直？

错解分析：直线方程的一般式包含了所有直线的方程，而斜截式只适用斜率存在的直线的方程，所以在把一般式化成斜截式时会漏解，做此类题目时应先考虑好斜率不存在的情况.

正解：当直线l1斜率不存在时，1-a=0，即a=1时，直线l1：3x-1=0与直线l2：5y+2=0垂直；

综上所述，当a=1或a=-1时，l1⊥l2.

点评：本题还有更简洁的方法，通过推导出两直线垂直的一般性结论：A1A2+B1B2=0来做，不需要分类讨论，就可以避开斜率不存在或斜率为0的情况，是两直线垂直的充要条件.