『失败』的『新』发现

☉江苏省扬州市邗江区蒋王中学 王 跃 曹松青

『失败』的『新』发现

☉江苏省扬州市邗江区蒋王中学 王 跃 曹松青

一、问题生成

在听一节数学复习课时，有些感悟，与大家共赏.下题为课上一道例题：

已知1，x1，x2，2成等差数列，1，y1，y2，2成等比数列，则点P1（x1，y1）、P2（x2，y2）在直线y=x的上方还是下方？

课堂上，老师直接运用等差数列、等比数列的定义分别计算出x1、x2、y1、y2的值，一路轻车快马，很快便判断出点P1（x1，y1）、P2（x2，y2）在直线y=x的下方.

直觉告诉笔者此处定然别有洞天，本以为教者会系舟登岸，引领笔者和学生到此一游，可这位船长却认为无甚风景，命令开往另处.只可惜“舰机轻轻过”之时，良机也轻轻过去了.心中也因此有了一个结，一时难以释怀，课后便独自踏上了探究之路.

二、问题探究

路在何方？当然不能走纯计算的老路，图像法自是首选.显然从函数图像的角度来看等差数列的通项公式an=a1+（n－1）d及等比数列的通项公式an=a1qn－1，二者皆有鲜明的几何形象.故只需在直线及函数y=a1qx－1的图像上适当取一些离散的点即可.

如图1，在直线y=x上取点A（1，1），B（2，2），再取线段AB的三等分点C1、C2，则由题意及等差数列的相关概念知C1、C2的坐标分别为 （x1，x1）、（x2，x2），过C1、C2点分别作x轴的垂线交函数y=a1qx－1的图像于点P1、P2，则由题意及等比数列的相关概念知点P1、P2的坐标分别为（x1，y1）、（x2，y2），由图便可直观地看出点P1（x1，y1），P2（x2，y2）在直线y=x的下方.

图1

进一步思考：若b＞a＞0，且a，x1，x2，…，xn－1，b成等差数列，a，y1，y2，…，yn－1，b成等比数列，则点Pi（xi，yi）（1≤i≤n－1）在直线y=x的上方还是下方？

通过类比可作大胆猜想：点Pi（xi，yi）（1≤i≤n－1）在直线y=x的上方，即xi＞yi.

不妨设上述等差数列的公差为d，等比数列的公比为q，

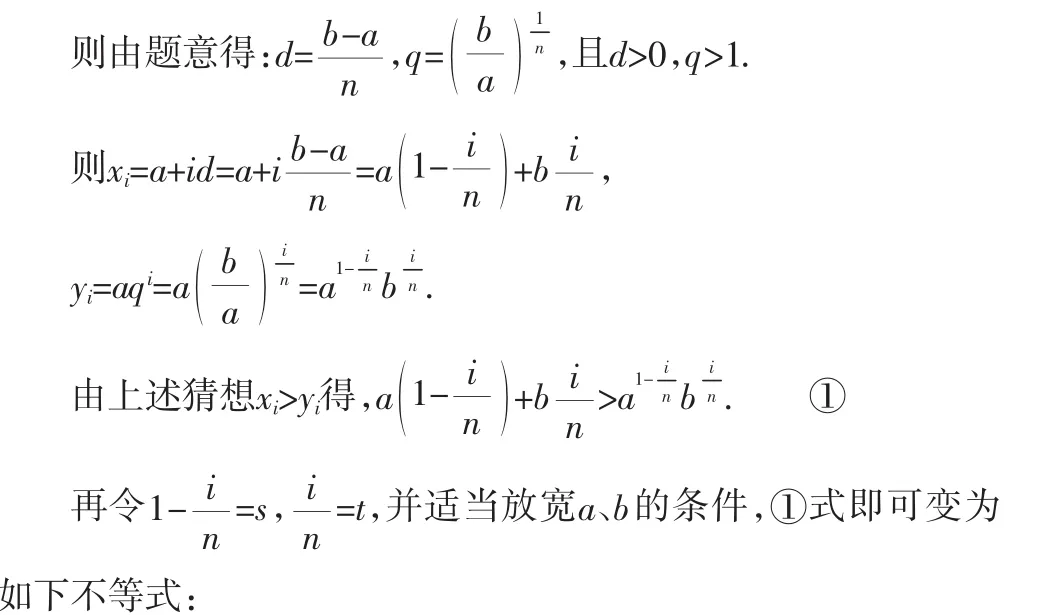
若a，b，s，t皆为正数，且s+t=1，则有as+bt≥asbt. ②

②式仅是猜想，尚需证明.

考虑到不等式②与著名的伯努利不等式结构上的相似性，故尝试用伯努利不等式证明.

附伯努利不等式：设x＞1，a∈R，

至此证明大功告成.此不等式可谓简约而不简单，更令人惊奇的是它竟可视为基本不等式的推广.

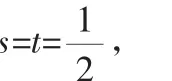
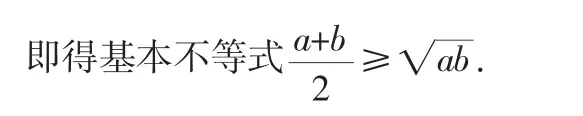
数学的简洁美、统一美由此可窥一斑.

三、问题反思

面对如此神奇的不等式，不由心生疑惑：是它一直“养在深闺无人识”还是笔者孤陋寡闻？在疑惑中，成就感和幸福感油然而生.隔日到图书馆一查资料，方知原是赫尔德不等式的变形.甚是失望，但转念一想：笔者的发现之路若与大师不同，则有个人特色，自是别开生面；若是历史的重演，则大师“于我心有戚戚焉”.这样想来，不免自鸣得意.回首发现之旅，从特殊到一般，以有涯逐无涯，从显在的线索追寻潜在的真相，其间苦乐参半，好不艰难！何等痛快！而最终简单的问题竟包含着深刻的思想和方法，不由唏嘘不已，浮想联翩：

倘若笔者没有一点“不走寻常路”的决心，恐会“入宝山而空返”；

倘若以为研究下去可能会吃别人嚼过的馍，没意思，则也不会有如此独特的心灵摇曳；

倘若那位上课教师能够不囿于让学生解出题目，而是以“解法不优誓不休”的信念，充分挖掘问题中的教学资源，引领学生经历“一场场风霜雪雨”，继而“踏平坎坷成大道”，则学生的创新能力也必然在其间潜滋暗长；

倘若学生把这种数学的思维方法内化为一种习惯，把在探究中形成的坚韧、执着内化为一种品格，也必将受用终身；

倘若笔者现在去讲课，再也不会轻易选择难题让学生去探究.因为那样，大多数学生常常因为门槛太高而袖手旁观.自己可能只抓来一些小题，如烹小鲜般的加以料理，希望它鱼小味不小，也希望学生吃得津津有味.更希望他们在以鱼为食的同时，以渔立业.

倘若笔者不去听课，便不能换个角色以听课者的眼光去发现问题.事实上，发现问题远比解决问题重要得多，当我们在教研中苦于找不到研究课题时，不妨去听听课，课堂永远是蕴藏问题的宝库.