识辨究——谈某点处导数与切线的关系

☉江苏省江阴高级中学 戴 颖

识辨究
——谈某点处导数与切线的关系

☉江苏省江阴高级中学 戴 颖

数学发展的里程碑之一是微积分的创立，它的发展和广泛应用开拓了数学的新纪元，为现代数学的过渡创造了一个新的研究工具，为变量和函数研究开拓了不可估量的贡献．导数是其一个核心的内容，在高中数学中“几起几落”，旧版教材中曾经由极限引入导数，改版后又将极限删除，但是导数作为核心部分一直保留下来，可以看出教材的编者对其重视程度．

初等微积分在世界各地基本上都已进入高中教材．2003年教育部颁布的《普通高中数学课程标准（实验）》把微积分初步规划于选修系列1（文科）、2（理科），但是出乎意料的是，新教材对微积分初步的编排有悖于传统教材的编排，旧版教材是按照“极限——连续——导数——微分——积分”的关系呈现，而新教材是以“变化率——导数——积分”的顺序编排．笔者两种版本都教授过，应该说各有利弊，在教学中发现一个有趣的问题：学生对于其中某一点处导数存在与否都是不理解的，尤其以新教材教授的学生为甚（大概就是因为新教材删去了极限）．

针对这一有趣的问题，笔者就苏教版《高中数学选修2-2》（以下简称“新教材”）中对关于函数在某一点处是否可导以及切线的存在提出自己的教学想法，供大家参考．

一、导数概念的深入理解

教材给出的导数定义略显简易．因为导数即为割线斜率的极限值，所以可以仿照单点极限而详细化导数的定义1：

这是首先要解决的导数概念细化的问题，便于接下去的讨论．

二、基本初等函数

高中教材中对函数在某一点处连续是这样下的定义2：

（1）函数f（x）在x0处有定义；

（2）函数f（x）在x0处有极限；

导数教学中，有这样一个定理：连续不一定可导，而可导一定连续．一线教师都有这样的亲身经历，其实，学生不太理解这句话．因此也解决不了实际问题．

从高中数学的基本初等函数来说，比如：“正比例函数、多项式函数、指数函数、对数函数、正弦函数、余弦函数”等，函数在定义域内某点处，处处连续，但并非处处可导，但切线是否处处存在呢？对于一般的点当然没有问题，不妨看些特殊的点．

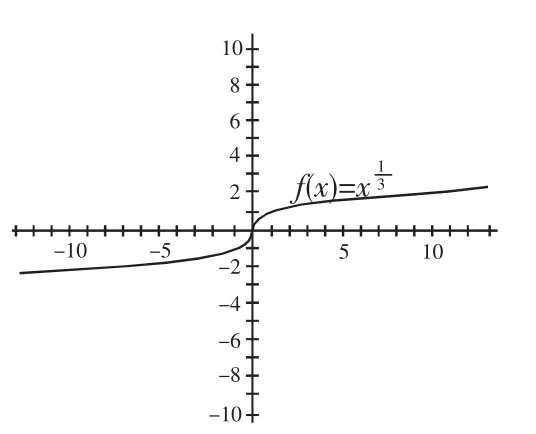
图1

问题1如图1，函数（fx）=是基本初等函数之一的幂函数．函数（fx）在x=0处显然连续，但右导数不存在，同样左导数不存在，因此函数f（x）在x=0处不可导．但进一步思考：函数f（x）在x=0处的切线存在吗？尽管有点超越高中数学的要求，但对爱思考的学生来说，是一种探究．为此，笔者想从两个方面来谈一谈．

1．加深理解切线的概念

中学生对切线的理解，是循序渐进的．在初中，一个学生认为直线与圆有一个交点称为相切；但在高中的圆锥曲线学习中，学生会知道双曲线和直线有一个交点，但并非相切；在大学数学中，微分曲线的研究不仅仅是二次曲线，切线和曲线的交点不止一个，所以不能用交点个数来定义，而是用割线的极限位置定义切线．

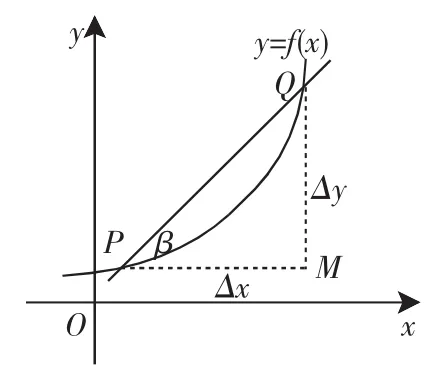
图2

2．切线的几何意义

定义3：若函数f（x）在点x0处连续，且在点x0处的左（或右）导数存在，则函数f（x）的图像在点（x0，f（x0））处的左（或右）半切线存在，且其斜率为f′－（x0）（或f′+（x0））．

图3

从问题1可知，常见的基本初等函数在某些特殊点处并非处处可导，但切线依旧存在．导数概念易从左（右）导数加深理解，切线的存在可从切线的几何意义以及左（右）半切线上领会．

三、分段函数（分界点处是连续的函数）

下文讨论分界点处连续的分段函数．（函数f（x）在x0处不连续必不可导、无切线）

分段函数是函数的重要组成部分，对分段函数在某一点处的导数与切线存在与否的探究，更深刻的理解上述问题1中所阐述的．举一个浅显的例子：

图4

把常见的分界点处连续的分段函数可导与切线问题以图5～8所示：

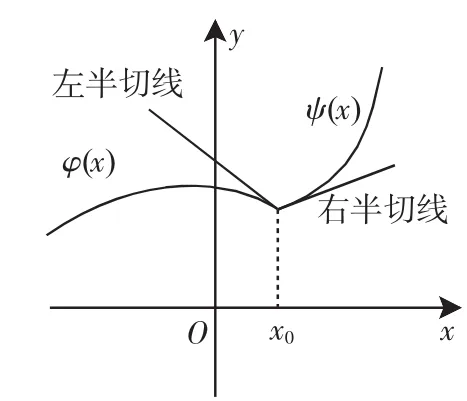
图5

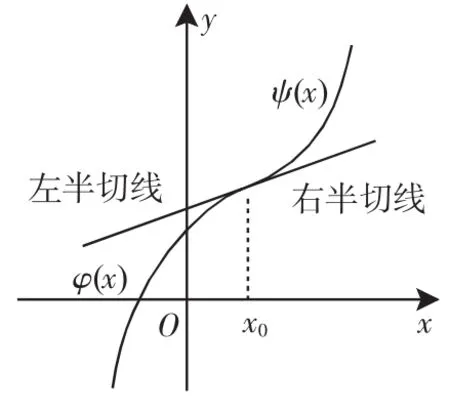
图6

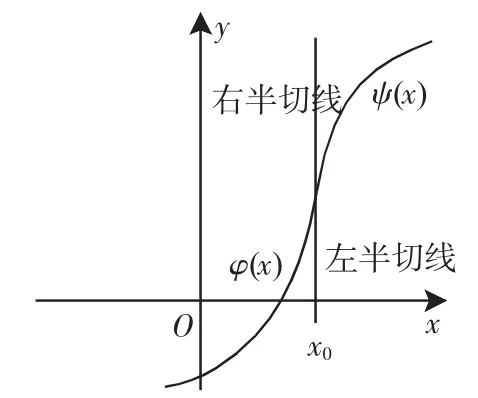
图7

图8

由图5可知：A≠B，左、右半切线不重合，f′（x0）不存在，切线不存在；由图6可知：A=B，左右半切线重合，f′（x0）存在，切线存在；由图7可知：A=B=+∞，且同号，f′（x0）不存在，但切线存在（问题1便是此类情形）；由图8可知：A=－∞，B为有限数，f′（x0）不存在，切线不存在．

为此，可以有结论：分界点x0处连续的分段函数，若点x0是f′（x）的跳跃间断点或无穷型间断点，则f（x）在点x0处一定不可导，切线不存在．

四、结束语

对于某一点处导数与切线的存在与否问题，尤其是一些较为的特殊点（往往也只对特殊的点才需要此类研究），一般可用左右导数来比较．

本文主要探讨高中常见基本初等函数在特殊点和分段函数在分界点连续的前提下，用左右导数值或左右半切线来判别导数的存在与否．将数形结合思想渗透其中，结合左右半切线的概念（对优秀学生适时引入），使其提高对切线的理解，从图像上进行了直观形象的解释，从思维上进行了一种突破．

希望通过此类探讨，使学生在对某一点处导数与切线存在与否的问题上有更深刻的认识和理解，对进一步学习导数打下扎实的基础．

1．中华人民共和国教育部．普通高中数学课程标准（实验）［M］．北京：人民教育出版社，2003．