“以大带小”式教学法在初中数学教学中的应用探究——以“多边形及其内角和”教学为例

☉江西省兴国县东村中学 刘衍锋

“以大带小”式教学法在初中数学教学中的应用探究
——以“多边形及其内角和”教学为例

☉江西省兴国县东村中学 刘衍锋

何谓“以大带小”式教学法，即在教学中教师通过设计几个探究性大问题来引导学生进行探究，在探究过程中以小问题来进行辅助的教学法．“以大带小”式教学法是基于教案教学而进行的，对突出教师的主导性和学生的主体性都具有积极作用．在“以大带小”式教学法中一般可按照导入迁移、设疑探究、合作总结、练习拓展几个步骤进行．

一、导入迁移

导入一般通过创设情景来引导学生从直观向抽象过度，为新知的学习打下基础．迁移则是根据数学知识连续性的特点，在对旧知识进行复习的基础上迁移到新知识的学习，促进学生形成系统联系的知识链．

在“多边形及其内角和”的教学中，教师可首先以幻灯片的形式来呈现生活中如瓷砖、五角大楼等各种不同形状的图片，然后由这些图片转换为抽象的图形．接着以问题“三角形的内角和是多少？还记得我们是怎么求证的吗”来引入对三角形内角和定理的复习．此时教师可根据学生的发言展示证明过程．如图1，过A点作PQ∥BC，则∠B=∠1，∠，C=∠2．

因为∠1+∠BAC+∠2=180°，所以∠B+∠BAC+∠C=180°．

一般导入迁移时间不宜过长，以3～5分钟为宜，重点是要引导学生从旧知识到新知识的过渡．如该课时中，展示三角形的内角和求证过程后，以问题“三角形的内角和是180°，那么，我们能不能用同样的方法来求证四边形、五边形、六边形……n边形的内角和呢？”接着板书课题，引入新知识探究．

图1

二、设疑探究

在探究阶段，教师要根据教学内容而设计出相应的探究性问题，在多边形的内角和探究中，要让学生由此及彼的得到多边形的内角和．在对三角形内角和求证过程的推导基础上，教师可用四边形的内角和推导过程来进行引导，从而逐步过渡到对多边形内角和的求证．在具体操作中，教师要用问题来逐步引导，具体操作如下：

如图2，连接AC，四边形ABCD的内角和等于两个三角形内角和的和，即180°×2=360°．

设大问1：多边形的内角和与各三角形内角和之间的关系，三角形个数与多边形边数的关系？

……设大问2：n边形有（？－2）个三角形，内角和是180°×（？－2）．设小问1：三角形内角和为180°×（3－2）=180°，四边形内角和为180°×（4－2）=360°，那么，五边形该如何表示？

设小问2：如果是多边形呢？内角和又该如何求解？

接着进入小组探究过程．在小组探究过程中，教师要引导学生通过动手画、动脑思考、动嘴说来完成．同时，在辅导过程中，教师要深入到每一个小组，就学生在探究中所遇到的问题进行引导．如有的学生在探究中没有从规律上进行探究，而是提出了五边形的内角和求证方法，此时教师在鼓励的同时要给予方法指导，同时要让学生从规律上来进行探究，掌握科学的探究方法．

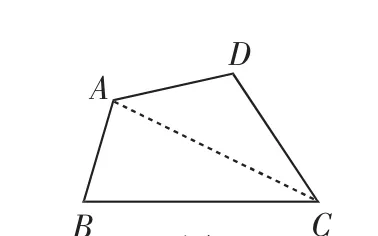
图2

三、合作总结

在合作总结中，主要目的是结合学生的探究过程，将各个小组的探究结果进行汇总，从而形成一致性认识．在总结过程中，教师要更多关注学生的主体性，让各个小组充分发言，在小组代表发言的基础上教师再进行总结．当然，在总结过程中，教师还需以问题来作为引导．如在该课时的总结过程中，教师所设问题如下：

设大问1：在探究中你获得了什么发现？还遇到了什么困难？

此时的小问就交给了学生．

法

设大问2：还有什么方法可以求证多边形的内角和？

根据学生探究中所涉及的不同方法而设以下小问．

设小问1：三角形的个数与多边形边数有何关系？（比边数少2）

设小问2：在多边形内任取一点O，顺次连接各顶点你发现多边形的内角和有什么规律？（等于所有三角形的内角和减去1周角）

四、练习拓展

练习拓展是为了对所学新知识进行巩固，同时引导学生由知识向技能过度．在练习中提倡当堂学习，让学生学以致用．练习题的设计在保证对新知识进行巩固的同时要适当拓展．如已知边数如何求内角和；已知内角和如何求边数；n边形的内角和与外角和成一定的比例关系，求其n边形的边数．目的是要让学生能做到举一反三．

例 多边形的内角和公式与三角形内角与外角的关系？

如图3，求∠A+∠ABC+∠C+∠D+∠E+∠F=？

图3

分析：根据四边形的内角和等于360°，及三角形一个外角等于和它不相邻的两个内角的和得出．

解：在四边形BEFG中，

因为∠EBG=∠C+∠D，∠BGF=∠A+∠ABC，

所以∠A+∠ABC+∠C+∠D+∠E+∠F=∠EBG+∠BGF+∠E+∠F=360°．

笔者在教学中对“以大带小”式教学法也还处于研究和实践阶段，在今后教学中还需不断总结和完善．在这里提出该教学方法，旨在抛砖引玉，希望能对同行们有所启示．

1．白瑞媛．初中数学课堂教学有效性研究［D］.呼和浩特：内蒙古师范大学，2011．

2．陈玲玲．浅谈初中数学导学案的设计［J］.小作家选刊，2011，6．

3．陈建军．新课改下初中数学误区新议［J］.中国科教创新导刊，2009，21．