操作让考题生辉

☉江苏省连云港市中云中学 王亚玲

随着中考命题的进一步深化与改革，各地中考命题都不同程度地利用题目的不同结构形式和呈现方式来考查学生的各种潜能，成为当前中考命题的主流.在2011年各地中考试题中，不少地市通过不同的操作形式创设试题情境，使试题活灵活现，栩栩如生.所谓“操作型试题”就是命题者通过让学生读题、动手操作进行体验试题的内涵，进而观察、分析、思考、归纳解决问题的思路和方法.此类问题往往是把学生放置于手、脑皆动的环境中，让学生亲临其境，凸显试题的存在性、应用性，体现以人为本，注重发展学生数学思维的能力.

一、命题者语言叙述，学生进行画图

例1（2011年甘肃兰州）如图1，在单位长度为1的正方形网格中，一段圆弧经过网格的交点A、B、C.

（1）请完成如下操作：

①以点O为原点、竖直和水平方向所在的直线为坐标轴、网格边长为单位长，建立平面直角坐标系；②用直尺和圆规画出该圆弧所在圆的圆心D的位置（不用写作法，保留作图痕迹），并连接AD、CD.

（2）请在（1）的基础上，完成下列问题：①写出点的坐标：C______、D______.②⊙D的半径=______（结果保留根号）.

③若扇形ADC是一个圆锥的侧面展开图，则该圆锥的底面面积为______（结果保留π）.

④若E（7，0），试判断直线EC与⊙D的位置关系，并说明你的理由.

图1

思路分析：（1）①作出AB和BC的垂直平分线，交点就是圆心D.

（2）②在Rt△AOD中应用

勾股定理求解.③弧ABC的长就是圆锥的底面圆周长，观察图形易得∠ADC=90°，弧长为底面半径为，底面面积为④从图上易看出是相切，证明时需证∠DCE=90°，注意到线段CD、CE、DE的长均可求出，故用勾股定理的逆定理.

方法规律：建立平面直角坐标系的关键是确定原点和坐标轴；尺规作图作圆弧的圆心，依据是弦的垂直平分线必过圆心，则不平行的两弦的垂直平分线的交点就是圆心；证切线时要看该线是否经过圆上的点，若是则证该线垂直于过该点的半径，若不是就要证圆心到该线的距离等于半径.

二、命题者设计程序，让学生判断结论

例2（2011年遵义）有一数值转换器，原理如图2所示，若开始输入x的值是5，可发现第一次输出的结果是8，第二次输出的结果是4……请你探索第2011次输出的结果是____.

图2

思路分析：由转换器的程序可知，第三次输出为2，第四次为1，第五次为4，第六次为2……从中得到除第一次外，后面是4，2，1循环变化，（2011-1）÷3的余数为2，所以与规律中的第二个相同，即为2.

方法规律：探究规律的问题，应先通过计算把前面几个数据算出来，然后再从中找出一般规律.

三、命题人提供示意图，让学生抽象结论

例3（2011年江苏宿迁）一个边长为16m的正方形展厅，准备用边长分别为1m和0.5m的两种正方形地板砖铺设其地面.要求正中心一块是边长为1m的大地板砖，然后从内到外一圈小地板砖、一圈大地板砖相间镶嵌（如图2所示），则铺好整个展厅地面共需要边长为1m的大地板砖____块.

思路分析：根据题意可知大地板砖由里向外共铺设了6圈，每圈所用地板砖的个数依次为1、12、24、36、48、60，故铺好整个展厅地面共需要边长为1m的大地板砖181块.

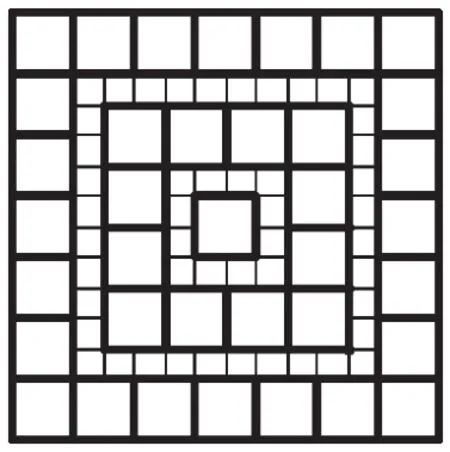
图3

方法规律：本题有两种探究方向.一是从里向外探究：第二圈的大正方形边长为4=1+3，用的地板砖共需要（4-1）×4=12块；第三圈的大正方形边长为7=1+3×2，用的地板砖共需要（7-1）×4=24块；第四圈的大正方形边长为10（=1+3×3），用的地板砖共需要（10-1）×4=36块；第五圈的大正方形边长为13=1+3×4，用的地板砖共需要（13-1）×4=48块；第六圈的大正方形边长为16=1+3×5，用的地板砖共需要（16-1）×4=60块，此时正好是正方形展厅的边长，也就铺设完整个展厅.由1+12+24+36+48+60=181，得到所求答案.

另一种探究方向是由外向里探究：最外一圈共需要大地板砖为（16-1）×4=60块，倒数第二层需要大地板砖铺设的正方形边长为16-3=13，共用地砖48块；倒数第三层需要大地板砖铺设的正方形边长为16-3×2=10，共用地砖36块；倒数第四层需要大地板砖铺设的正方形边长为16-3×3=7，共用地砖24块；倒数第五层需要大地板砖铺设的正方形边长为16-3×4=4，共用地砖12块；倒数第六层需要大地板砖铺设的正方形边长为16-3×5=1，共用地板砖1块.故一共需要60+48+36+24+12+1=181（块）.

综上所述，数学教学应该将课本中一些静态的定理、法则、习题等动态化，在动感中探索，激活学生的思维，在新情境中让学生通过动手操作、观察思考进行解决问题，掌握学习数学的精髓.